11.2.1第1课时三角形的内角和定理 习题课件
文档属性
| 名称 | 11.2.1第1课时三角形的内角和定理 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 00:00:00 | ||
图片预览





文档简介
(共23张PPT)
知识要点全练
夯臭基础
知识点1三角形内角和定理
1.如图,在△ABC中,∠A=60°,∠B=40°,则
∠C等于
A.100°B.80
C.60
D.40
(第1题图)
(第2题图
60°
40
B
B
(第1题图)
(第2题图)
2.如图,在△ABC中,∠A=50°,∠ABC=70°,BD
平分∠ABC,则∠1的度数是
A.85°
B.80°
C.75°
D.70°
3.三角形的三个内角的度数之比为2:3:4,那么这
个三角形是
(B)
A.直角三角形
B.锐角三角形
C.钝角三角形
D.等边三角形
4.(锦州)如图,AC与BD交于点O,AB∥CD,
∠AOB=105°,∠B=30°,则∠C的度数为
A.45°
B.55°
C.60
D.75°
(第4题图)
(第5题图)
(第6题图)
D、zC
∠46°54X
SB B
D
c B
第4题图)
(第5题图)
(第6题图)
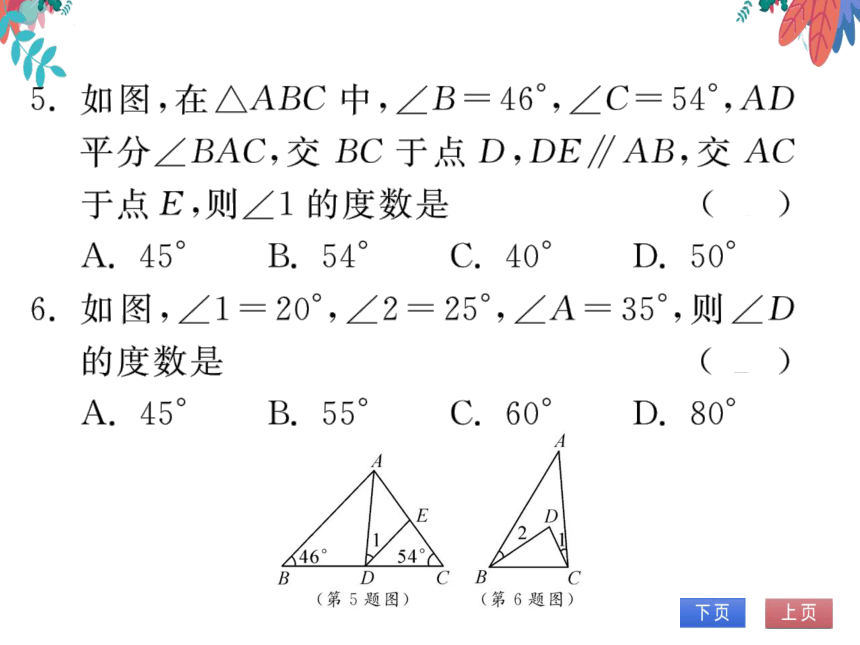
5.如图,在△ABC中,∠B=46°,∠C=54°,AD
平分∠BAC,交BC于点D,DE∥AB,交AC
于点E,则∠1的度数是
A.45°
B.54°
C.40°
D.50°
6.如图,∠1=20°,∠2=25°,∠A=35°,则∠D
的度数是
A.45
B.55°
C.60
D.80°
E
46°
54
B
D
C B
(第5题图)
(第6题图)
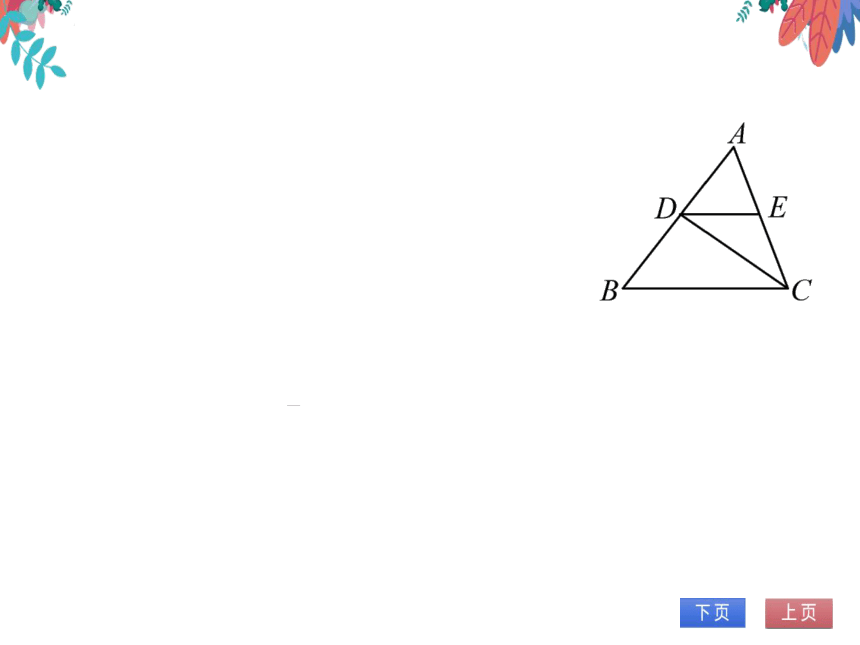
解:在△ABC中,∠A=60
∠B=50°,∴∠ACB=180
50-60=70
∴CD平分∠ACB,
∠BCD=∠ACB=35
∴DE∥BC,
∠EDC=∠BCD=35°
在△BDC中,∠BDC=180°-∠B-∠BCD
180-50-35=95
综上,∠EDC=35°,∠BDC=95
知识点2三角形内角和定理的应用
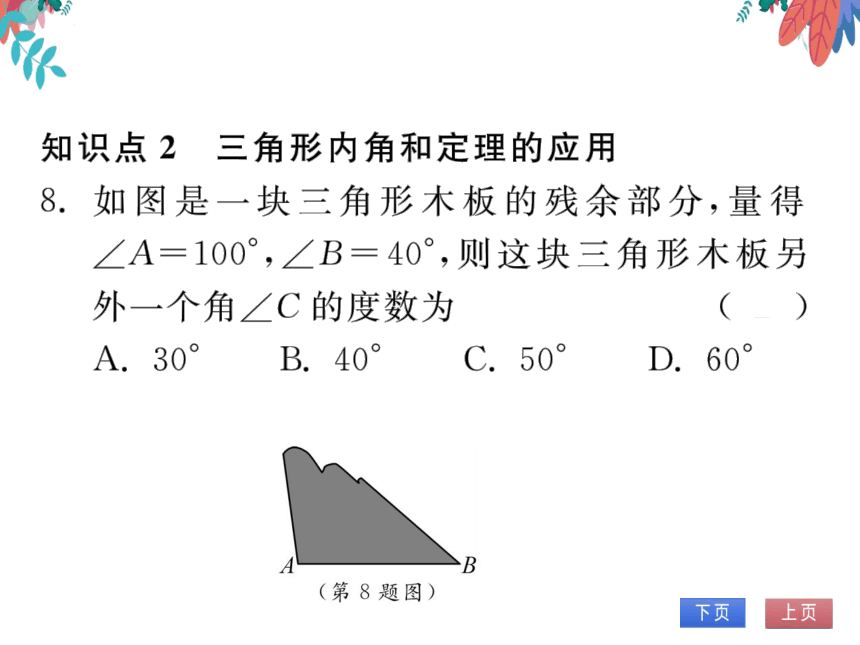
8.如图是一块三角形木板的残余部分,量得
∠A=100°,∠B=40°,则这块三角形木板另
外一个角∠C的度数为
(B)
A.30°
B.40°
C.50
D.60°
B
(第8题图)
(第9题图)
北
北
O
130
B
R
(第8题图)
(第9题图)
10.如图,按规定,一块模板中AB,CD的延长线
应相交成85°的角.因交点不在板上,不便测
量,工人师傅连接AC,测得∠BAC=32°
DCA=65°,此时AB,CD的延长线相交所成
的角是不是符合规定 为什么
知识要点全练
夯臭基础
知识点1三角形内角和定理
1.如图,在△ABC中,∠A=60°,∠B=40°,则
∠C等于
A.100°B.80
C.60
D.40
(第1题图)
(第2题图
60°
40
B
B
(第1题图)
(第2题图)
2.如图,在△ABC中,∠A=50°,∠ABC=70°,BD
平分∠ABC,则∠1的度数是
A.85°
B.80°
C.75°
D.70°
3.三角形的三个内角的度数之比为2:3:4,那么这
个三角形是
(B)
A.直角三角形
B.锐角三角形
C.钝角三角形
D.等边三角形
4.(锦州)如图,AC与BD交于点O,AB∥CD,
∠AOB=105°,∠B=30°,则∠C的度数为
A.45°
B.55°
C.60
D.75°
(第4题图)
(第5题图)
(第6题图)
D、zC
∠46°54X
SB B
D
c B
第4题图)
(第5题图)
(第6题图)
5.如图,在△ABC中,∠B=46°,∠C=54°,AD
平分∠BAC,交BC于点D,DE∥AB,交AC
于点E,则∠1的度数是
A.45°
B.54°
C.40°
D.50°
6.如图,∠1=20°,∠2=25°,∠A=35°,则∠D
的度数是
A.45
B.55°
C.60
D.80°
E
46°
54
B
D
C B
(第5题图)
(第6题图)
解:在△ABC中,∠A=60
∠B=50°,∴∠ACB=180
50-60=70
∴CD平分∠ACB,
∠BCD=∠ACB=35
∴DE∥BC,
∠EDC=∠BCD=35°
在△BDC中,∠BDC=180°-∠B-∠BCD
180-50-35=95
综上,∠EDC=35°,∠BDC=95
知识点2三角形内角和定理的应用
8.如图是一块三角形木板的残余部分,量得
∠A=100°,∠B=40°,则这块三角形木板另
外一个角∠C的度数为
(B)
A.30°
B.40°
C.50
D.60°
B
(第8题图)
(第9题图)
北
北
O
130
B
R
(第8题图)
(第9题图)
10.如图,按规定,一块模板中AB,CD的延长线
应相交成85°的角.因交点不在板上,不便测
量,工人师傅连接AC,测得∠BAC=32°
DCA=65°,此时AB,CD的延长线相交所成
的角是不是符合规定 为什么
