11.2.2三角形的外角 习题课件
图片预览


文档简介
(共12张PPT)
知识要点全练
夯奥基础
知识点1三角形外角的性质
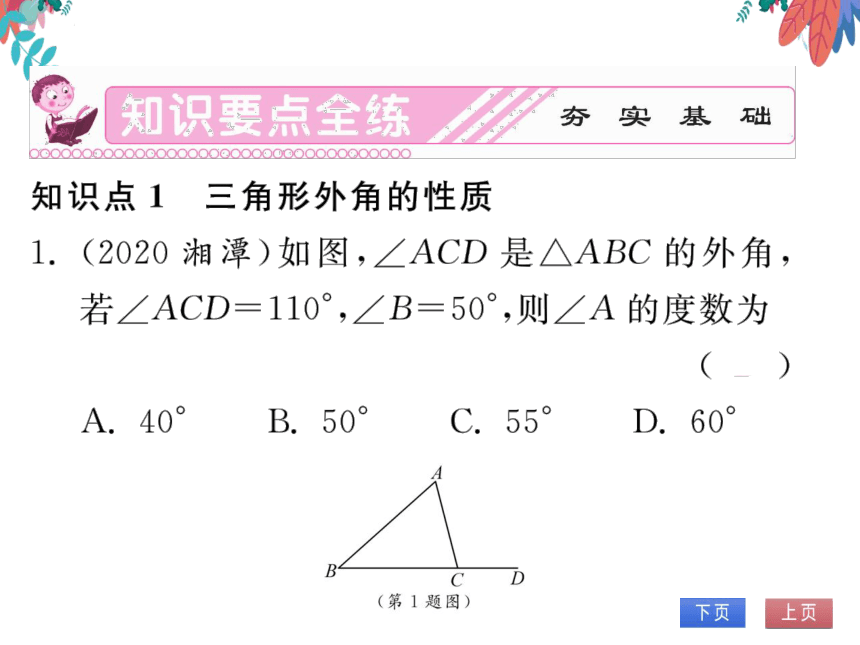
1.(2020湘潭)如图,∠ACD是△ABC的外角,
若∠ACD=110°,∠B=50°,则∠A的度数为
A.40°
B.50°
C.55
D.60°
(第1题图)
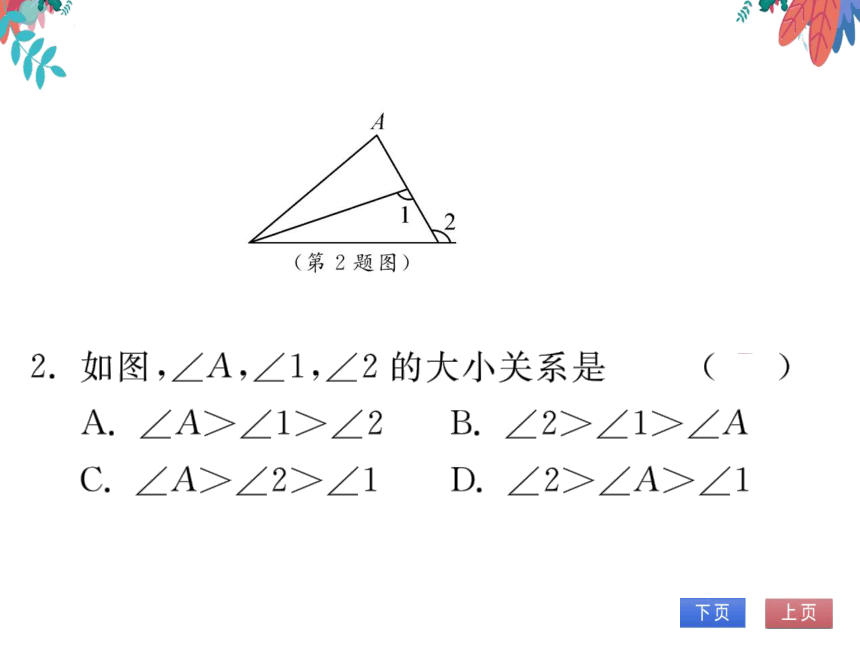
(第2题图)
2.如图,∠A,∠1,∠2的大小关系是
(B)
A.∠A>∠1>∠2B.∠2>∠1>∠A
C.∠A>∠2>∠1D.∠2>∠A>∠1
B
D
2
第1题图)
(第2题图)
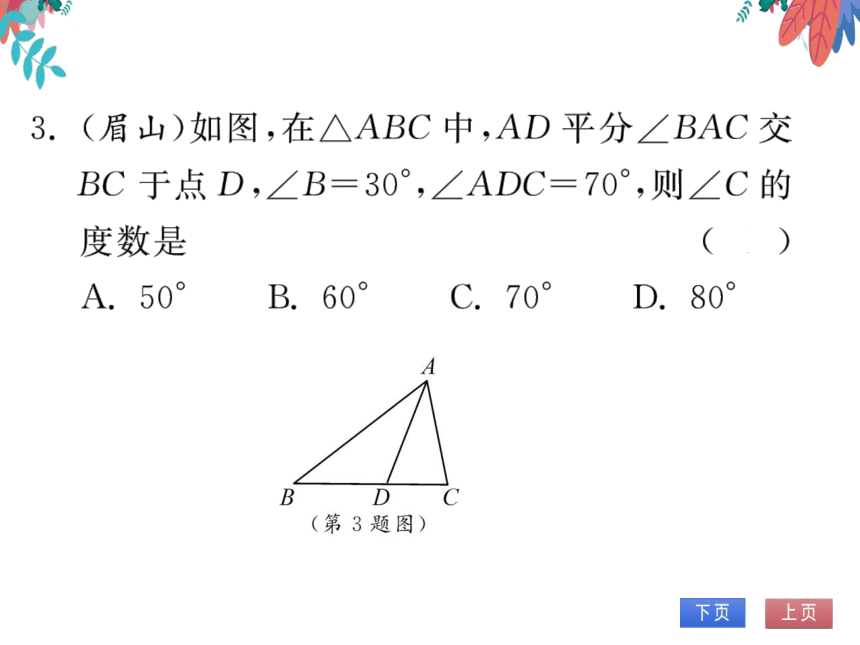
3.(眉山)如图,在△ABC中,AD平分∠BAC交
BC于点D,∠B=30°,∠ADC=70°,则∠C的
度数是
A.50°
B.60°
C.70°
D.80°
A
(第3题图)
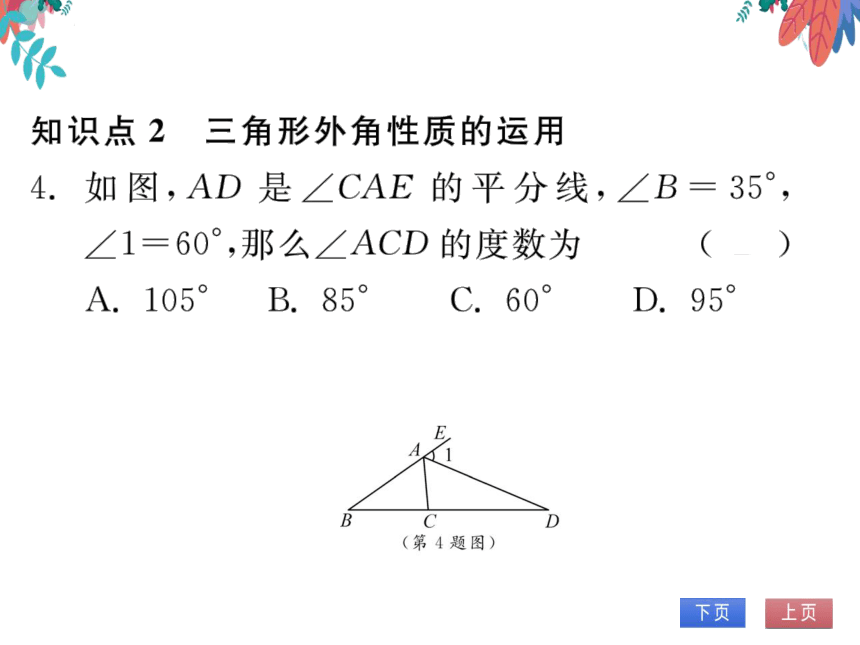
(第4题图)
D
(第3题图)
第4题图)
知识点2三角形外角性质的运用
4.如图,AD是∠CAE的平分线,∠B=35°,
1=60°,那么∠ACD的度数为
A.105°B.85
C.60
D.95°
5.如图,已知l1∥l2,∠A=40°,∠1=60°,则∠2
的度数为
A.40°
B.60°
C.80°
D.100
(第5题图)
(第6题图)
45°
2
30
B
(第5题图)
(第6题图)
6.(枣庄)将一副直角三角板按如图所示的位置
摆放,若含30°角的三角板的一条直角边和含
45°角的三角板的一条直角边放在同一条直线
上,则∠a的度数是
A.45°
B.60
D.85
如图,在锐角△ABC中,BE⊥AC,CD⊥AB,
垂足分别为E,D,且BE,CD相交于点P,若
∠A=50°,则∠BPC的度数为
A.150°B.130°C.120°D.100
规律方法全练
提升能力
8.如图,已知在△ABC中,BD,CE分别平分
∠ABC和∠ACB,∠1=20°,∠2=80°.求∠3
的度数
解:·BD平分∠ABC,
CBD
1=20
∠ABC=20+20°=40
BCD+∠CBD+∠2=180°,
∠BCD=180-200-80°=80°
CE平分∠ACB,
∠BCE=∠ACB=×800=40
∠3=∠ABC+∠BCE=40°+40°=80
探究创新全练
挑战自我
9.如图,在△ABC中,点D在BC边上,∠1
∠2,∠3=∠4,∠BAC=72.求∠DAC的
度数
解
1+∠
且∠1=∠2,∠3=∠4,
∠3=∠4=2∠2
设∠1=∠2=x°,
则∠3=∠4=2x°,
∠DAC=720-x°
∠DAC+∠3+∠4=180°,
720-x+2x+2x°=180
36°.∴∠DAC=72°-36°=36°
知识要点全练
夯奥基础
知识点1三角形外角的性质
1.(2020湘潭)如图,∠ACD是△ABC的外角,
若∠ACD=110°,∠B=50°,则∠A的度数为
A.40°
B.50°
C.55
D.60°
(第1题图)
(第2题图)
2.如图,∠A,∠1,∠2的大小关系是
(B)
A.∠A>∠1>∠2B.∠2>∠1>∠A
C.∠A>∠2>∠1D.∠2>∠A>∠1
B
D
2
第1题图)
(第2题图)
3.(眉山)如图,在△ABC中,AD平分∠BAC交
BC于点D,∠B=30°,∠ADC=70°,则∠C的
度数是
A.50°
B.60°
C.70°
D.80°
A
(第3题图)
(第4题图)
D
(第3题图)
第4题图)
知识点2三角形外角性质的运用
4.如图,AD是∠CAE的平分线,∠B=35°,
1=60°,那么∠ACD的度数为
A.105°B.85
C.60
D.95°
5.如图,已知l1∥l2,∠A=40°,∠1=60°,则∠2
的度数为
A.40°
B.60°
C.80°
D.100
(第5题图)
(第6题图)
45°
2
30
B
(第5题图)
(第6题图)
6.(枣庄)将一副直角三角板按如图所示的位置
摆放,若含30°角的三角板的一条直角边和含
45°角的三角板的一条直角边放在同一条直线
上,则∠a的度数是
A.45°
B.60
D.85
如图,在锐角△ABC中,BE⊥AC,CD⊥AB,
垂足分别为E,D,且BE,CD相交于点P,若
∠A=50°,则∠BPC的度数为
A.150°B.130°C.120°D.100
规律方法全练
提升能力
8.如图,已知在△ABC中,BD,CE分别平分
∠ABC和∠ACB,∠1=20°,∠2=80°.求∠3
的度数
解:·BD平分∠ABC,
CBD
1=20
∠ABC=20+20°=40
BCD+∠CBD+∠2=180°,
∠BCD=180-200-80°=80°
CE平分∠ACB,
∠BCE=∠ACB=×800=40
∠3=∠ABC+∠BCE=40°+40°=80
探究创新全练
挑战自我
9.如图,在△ABC中,点D在BC边上,∠1
∠2,∠3=∠4,∠BAC=72.求∠DAC的
度数
解
1+∠
且∠1=∠2,∠3=∠4,
∠3=∠4=2∠2
设∠1=∠2=x°,
则∠3=∠4=2x°,
∠DAC=720-x°
∠DAC+∠3+∠4=180°,
720-x+2x+2x°=180
36°.∴∠DAC=72°-36°=36°
