12.1全等三角形 习题课件
图片预览



文档简介
(共28张PPT)
知识要点全练A
夯臭基础
知识点1全等形与全等三角形
1.下列图形中,全等的一对是
(B)
2.下列属于全等形的是
A.形状相同的两个图形
B.周长相等的两个图形
C.面积相等的两个图形
D.能够完全重合的两个图形
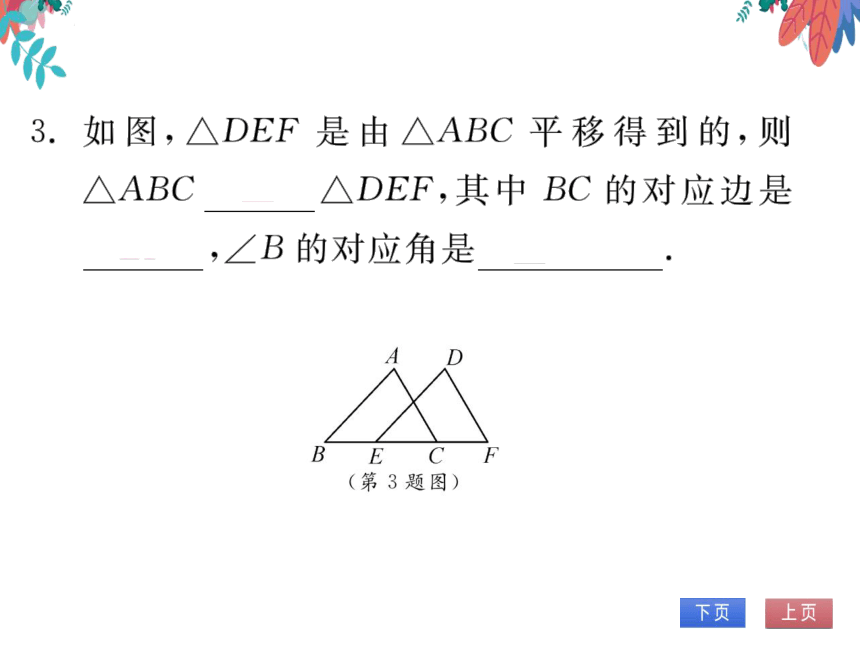
3.如图,△DEF是由△ABC平移得到的,则
△ABC≌△DEF,其中BC的对应边是
EF,∠B的对应角是DEF
(第3题图
(第4题图)
B E C F
(第3题图)
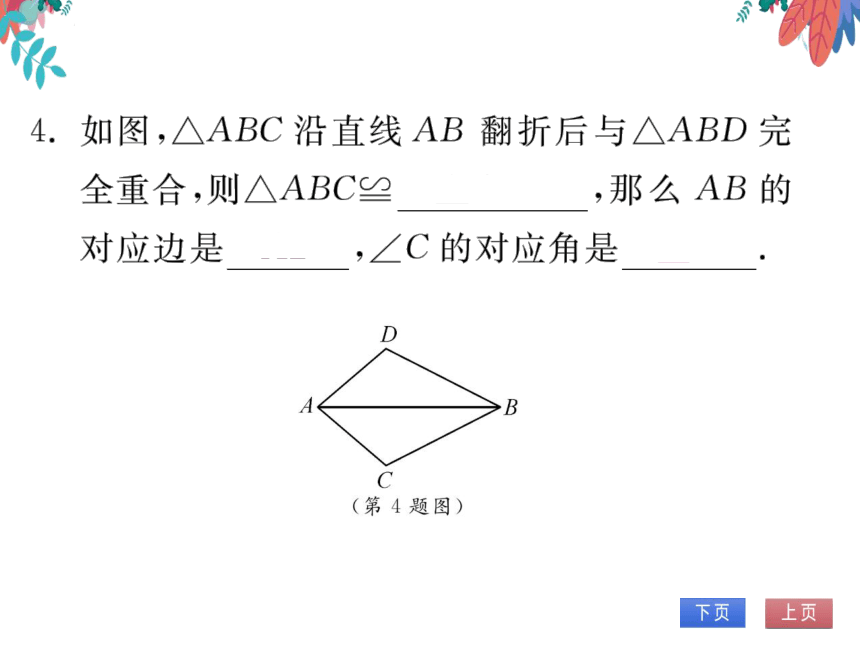
4.如图,△ABC沿直线AB翻折后与△ABD完
全重合,则△ABC≌△ABD,那么AB的
对应边是AB,∠C的对应角是∠D
B
(第4题图)
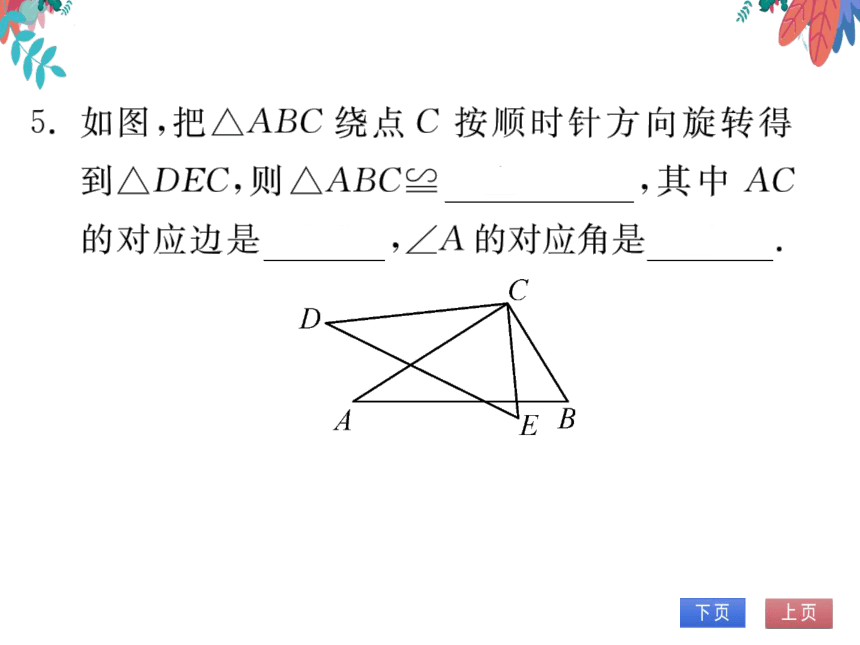
5.如图,把亼ABC绕点C按顺时针方向旋转得
到△DEC,则△ABC9△DEC,其中AC
的对应边是DC,∠A的对应角是∠D
知识点2全等三角形的性质
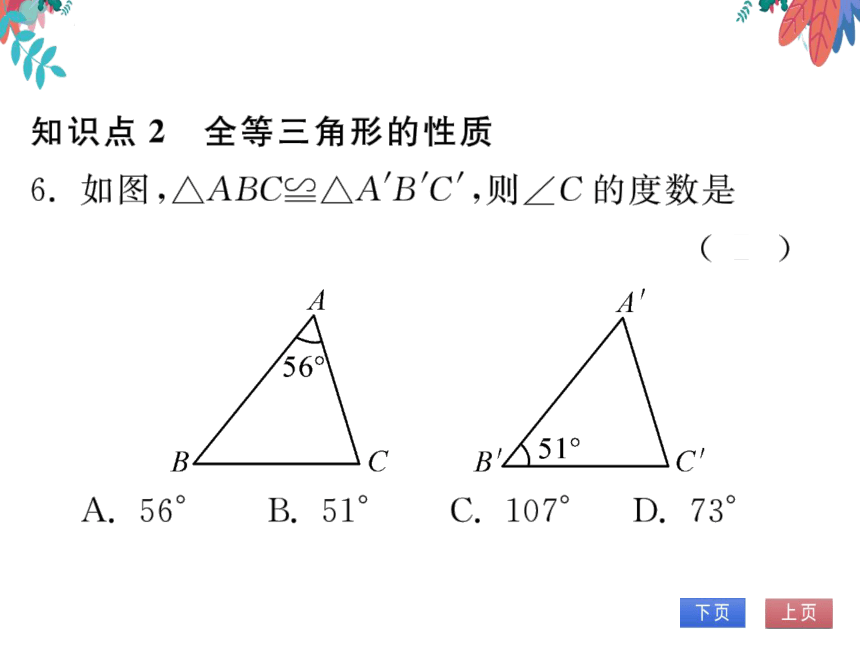
6.如图,△ABC≌△ABC,则∠C的度数是
A.56°
B.51°
C.107°D.73°
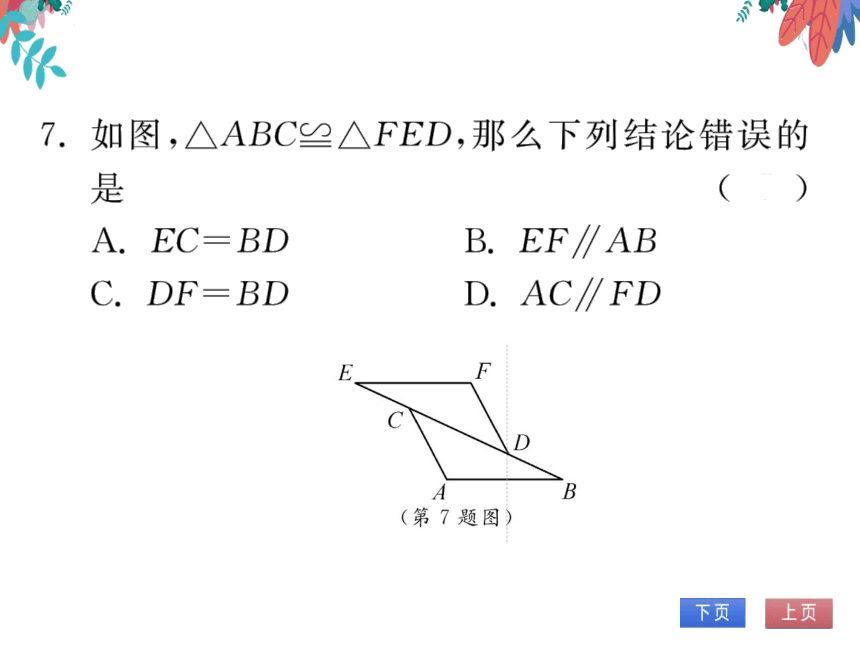
7.如图,△ABC≌△FED,那么下列结论错误的
疋
A. EC=BD
B.EF∥AB
C. DE=BD
D.AC∥FD
B
(第7题图)
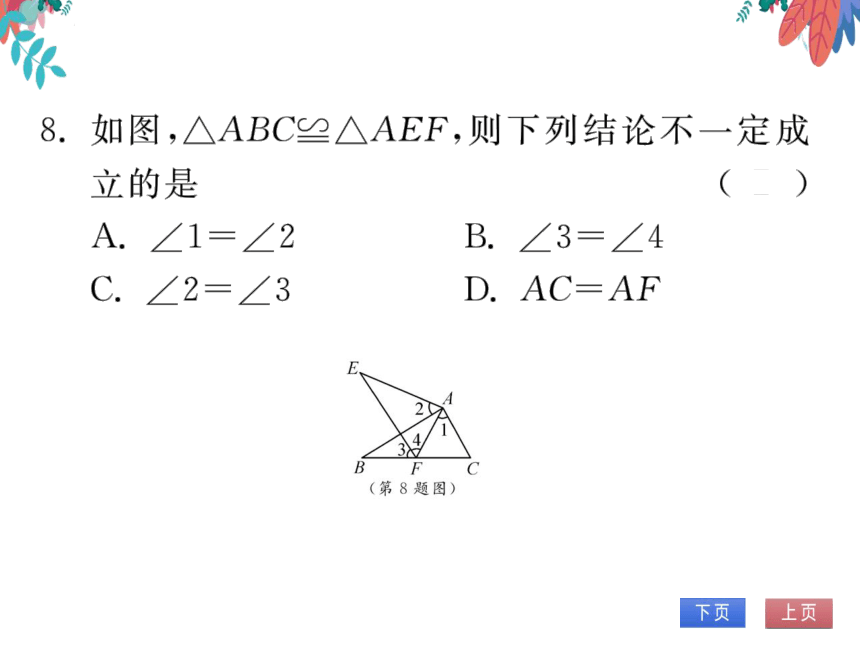
(第8题图)
F
(第7题图)
(第8题图)
8.如图,△ABC≌△AEF,则下列结论不一定成
立的是
A.∠1=∠2
B.∠3=∠4
C.∠2=∠3
D. AC=AF
9.如图,将△ABC绕点C按顺时针方向旋转40°
得到△A'B'C,若AC⊥A'B,则∠BAC的度
数为
A.50
B.60°
C.70
D.80°
(第9题图)
(第10题图)
10.如图,已知△ABE≌△ACD,AD=3,AC
∠ADC=110°,则BD
4,∠BEC
70
E
B
NC
(第10题图)
11.如图,在△ABC中,D为BC上一点,△ABD≌
△ACD,∠BAC=90
(1)求∠B的度数;
(2)判断AD与BC的位置关系,并说明理由
解:(1)∵△ABD≌△ACD
∠B=∠C
又∵∠BAC=90°,
∠B=∠C=4
(2)AD⊥BC
理由:∵△ABD≌△ACD
∠BDA=∠CDA
∠BDA+∠CDA=180°,
∠BDA=∠CDA=90
∴AD⊥BC
规律方法全练
提升能力
12.如图,将亼ABC沿BD翻折,使点A落在BC
上的点E处,再将△BDC沿DE翻折,点B
恰好落在点C处,则∠C的度数为(B
A.50
B.30°
C.25°
D.20°
(第12题图)
(第13题图)
知识要点全练A
夯臭基础
知识点1全等形与全等三角形
1.下列图形中,全等的一对是
(B)
2.下列属于全等形的是
A.形状相同的两个图形
B.周长相等的两个图形
C.面积相等的两个图形
D.能够完全重合的两个图形
3.如图,△DEF是由△ABC平移得到的,则
△ABC≌△DEF,其中BC的对应边是
EF,∠B的对应角是DEF
(第3题图
(第4题图)
B E C F
(第3题图)
4.如图,△ABC沿直线AB翻折后与△ABD完
全重合,则△ABC≌△ABD,那么AB的
对应边是AB,∠C的对应角是∠D
B
(第4题图)
5.如图,把亼ABC绕点C按顺时针方向旋转得
到△DEC,则△ABC9△DEC,其中AC
的对应边是DC,∠A的对应角是∠D
知识点2全等三角形的性质
6.如图,△ABC≌△ABC,则∠C的度数是
A.56°
B.51°
C.107°D.73°
7.如图,△ABC≌△FED,那么下列结论错误的
疋
A. EC=BD
B.EF∥AB
C. DE=BD
D.AC∥FD
B
(第7题图)
(第8题图)
F
(第7题图)
(第8题图)
8.如图,△ABC≌△AEF,则下列结论不一定成
立的是
A.∠1=∠2
B.∠3=∠4
C.∠2=∠3
D. AC=AF
9.如图,将△ABC绕点C按顺时针方向旋转40°
得到△A'B'C,若AC⊥A'B,则∠BAC的度
数为
A.50
B.60°
C.70
D.80°
(第9题图)
(第10题图)
10.如图,已知△ABE≌△ACD,AD=3,AC
∠ADC=110°,则BD
4,∠BEC
70
E
B
NC
(第10题图)
11.如图,在△ABC中,D为BC上一点,△ABD≌
△ACD,∠BAC=90
(1)求∠B的度数;
(2)判断AD与BC的位置关系,并说明理由
解:(1)∵△ABD≌△ACD
∠B=∠C
又∵∠BAC=90°,
∠B=∠C=4
(2)AD⊥BC
理由:∵△ABD≌△ACD
∠BDA=∠CDA
∠BDA+∠CDA=180°,
∠BDA=∠CDA=90
∴AD⊥BC
规律方法全练
提升能力
12.如图,将亼ABC沿BD翻折,使点A落在BC
上的点E处,再将△BDC沿DE翻折,点B
恰好落在点C处,则∠C的度数为(B
A.50
B.30°
C.25°
D.20°
(第12题图)
(第13题图)
