12.2第2课时用“SAS”证三角形全等 习题课件
文档属性
| 名称 | 12.2第2课时用“SAS”证三角形全等 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:17:17 | ||
图片预览







文档简介
(共27张PPT)
知识要点全练
夯臭基础
知识点1用“SAS”判定三角形全等
如图,AB=CB,DB=EB,要证明△ABE
△CBD,需要补充的条件是
A.∠D=∠E
C.∠1=∠2
D.∠A=∠C
(第1题图)
(第3题图)
E
E
B
(第1题图)
(第3题图)
下列各条件中,能使△ABC≌△DEF的条件
的是
A.AB=DE,∠A=∠D,BC=EF
B.AB=BC,∠B=∠E,DE=EF
C.AB=EF,∠A=∠D,AC=DF
D.BC=EF,∠C=∠F,AC=DF
3.如图,已知AB=AC,AD=AE,下列条件不能
判定△ABD≌△ACE的是
A. BD=CE
B.∠3=∠4
D.∠BAC=∠DAE
4.如图,有一块三角形的镜子,马虎不小心将其
打破成了1,2两块,现在需要配成同样大小的
块,为了方便起见,只要带上第1块,其
理由是两边和它们的夹角对应相等的两
个三角形全等
(第4题图)
5.(2020齐齐哈尔)如图,已知在△ABD和△ABC
中,∠DAB=∠CAB,点A,B,E在同一条直线
上,若使△ABD≌△ABC,则还需添加的一个条
件是AD=AC(答案不唯一)(只填一个
即可)
E
C
(第5题图)
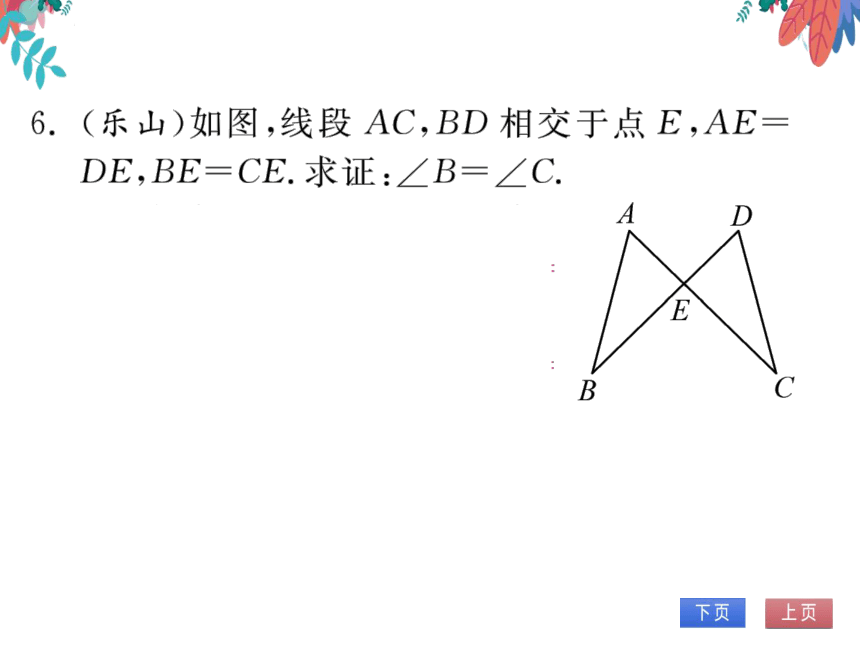
6.(乐山)如图,线段AC,BD相交于点E,AE
DE,BE=CE.求证:∠B=∠C
证明:在△AEB和△DEC中
AE=DE,BE=CE,∠AEB
DEC
△AEB≌△DEC,故∠B
知识点2全等三角形的判定(“SAS”)与性质的
综合应用
如图,AD,BC相交于点O,OA=OD,OB
OC.下列结论正确的是
A AD=BC
B.△AOB≌△DOC
A=∠C
D.∠B=∠D
B
D
(第7题图)
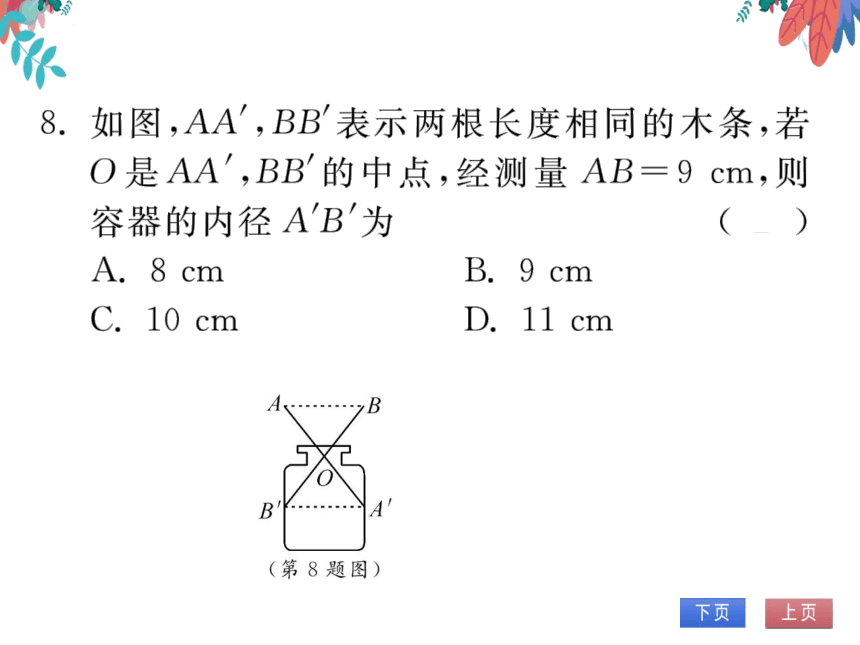
8.如图,AA,BB表示两根长度相同的木条,若
O是AA,BB的中点,经测量AB=9cm,则
容器的内径A'B为
(B)
A
8 cm
b.9 cm
C. 10 cm
D. 11 cm
9.如图,AD是△ABC的中线,E,F分别是AD
和AD延长线上的点,且DE=DF,连接BF,
CE,下列说法:①CE=BF;②S△ABD=S△ACD;
③BF∥CE;④△BDF≌△CDE.其中正确的
说法有
A.1个B.2个C.3个D.4个
B
D
(第9题图)
(第9题图)
(第10题图)
10.如图,AC⊥BD于点O,OB=OD,图中共有全
等三角形3对.
知识要点全练
夯臭基础
知识点1用“SAS”判定三角形全等
如图,AB=CB,DB=EB,要证明△ABE
△CBD,需要补充的条件是
A.∠D=∠E
C.∠1=∠2
D.∠A=∠C
(第1题图)
(第3题图)
E
E
B
(第1题图)
(第3题图)
下列各条件中,能使△ABC≌△DEF的条件
的是
A.AB=DE,∠A=∠D,BC=EF
B.AB=BC,∠B=∠E,DE=EF
C.AB=EF,∠A=∠D,AC=DF
D.BC=EF,∠C=∠F,AC=DF
3.如图,已知AB=AC,AD=AE,下列条件不能
判定△ABD≌△ACE的是
A. BD=CE
B.∠3=∠4
D.∠BAC=∠DAE
4.如图,有一块三角形的镜子,马虎不小心将其
打破成了1,2两块,现在需要配成同样大小的
块,为了方便起见,只要带上第1块,其
理由是两边和它们的夹角对应相等的两
个三角形全等
(第4题图)
5.(2020齐齐哈尔)如图,已知在△ABD和△ABC
中,∠DAB=∠CAB,点A,B,E在同一条直线
上,若使△ABD≌△ABC,则还需添加的一个条
件是AD=AC(答案不唯一)(只填一个
即可)
E
C
(第5题图)
6.(乐山)如图,线段AC,BD相交于点E,AE
DE,BE=CE.求证:∠B=∠C
证明:在△AEB和△DEC中
AE=DE,BE=CE,∠AEB
DEC
△AEB≌△DEC,故∠B
知识点2全等三角形的判定(“SAS”)与性质的
综合应用
如图,AD,BC相交于点O,OA=OD,OB
OC.下列结论正确的是
A AD=BC
B.△AOB≌△DOC
A=∠C
D.∠B=∠D
B
D
(第7题图)
8.如图,AA,BB表示两根长度相同的木条,若
O是AA,BB的中点,经测量AB=9cm,则
容器的内径A'B为
(B)
A
8 cm
b.9 cm
C. 10 cm
D. 11 cm
9.如图,AD是△ABC的中线,E,F分别是AD
和AD延长线上的点,且DE=DF,连接BF,
CE,下列说法:①CE=BF;②S△ABD=S△ACD;
③BF∥CE;④△BDF≌△CDE.其中正确的
说法有
A.1个B.2个C.3个D.4个
B
D
(第9题图)
(第9题图)
(第10题图)
10.如图,AC⊥BD于点O,OB=OD,图中共有全
等三角形3对.
