12.2第3课时用“ASA”和“AAS”证三角形全等 习题课件
文档属性
| 名称 | 12.2第3课时用“ASA”和“AAS”证三角形全等 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:17:17 | ||
图片预览



文档简介
(共28张PPT)
知识要点全练
夯奧基础
知识点1用“ASA”判定三角形全等
1.如图,线段AD,BC相交于点O,若OA=OB,
为了用“ASA”判定△AOC≌△BOD,则应补
充的条件是
(A)
A.∠A=∠B
B. AD=BC
C. AC=BD
D. OC=OD
B
(第1题图)
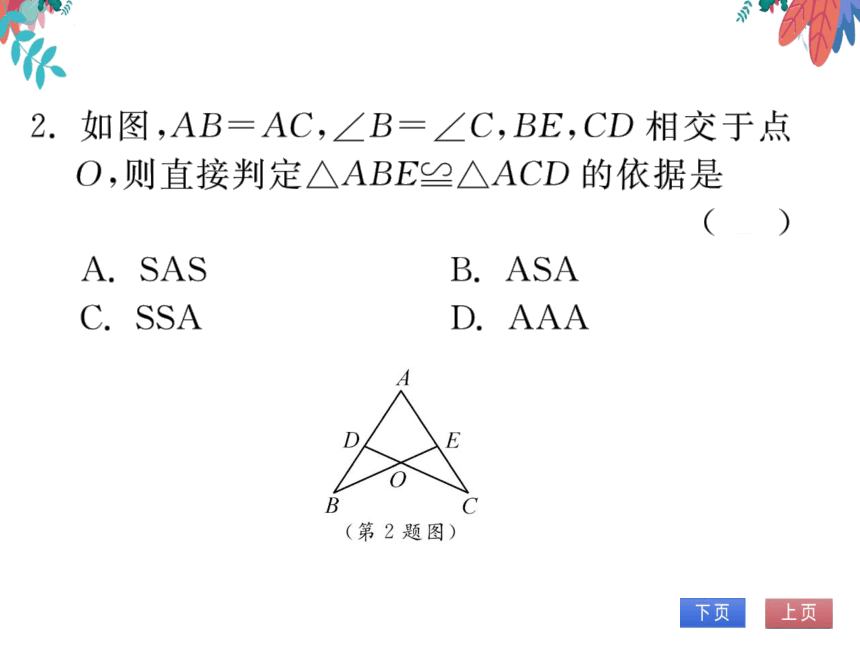
2.如图,AB=AC,∠B=∠C,BE,CD相交于点
O,则直接判定△ABE≌△ACD的依据是
A. SAs
B. ASA
C. SSa
D. AAA
3.如图,某同学不小心把一块三角形玻璃打碎成
块,现在要到玻璃店配一块与原来完全相同
的玻璃,最省事的方法是
A.带①和②去
B.只带②去
C.只带③去
D.都带去
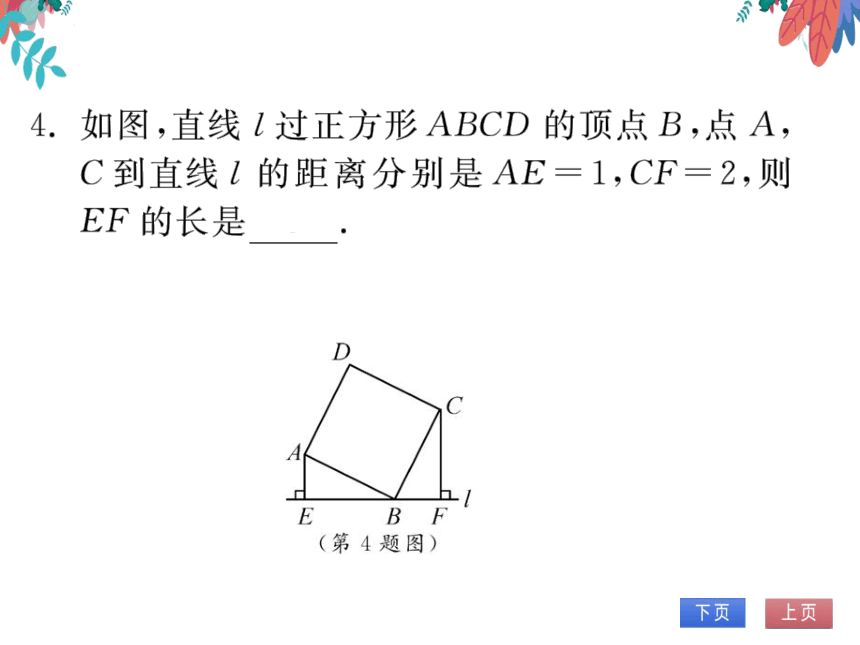
4.如图,直线l过正方形ABCD的顶点B,点A,
C到直线l的距离分别是AE=1,CF=2,则
EF的长是3
(第4题图)
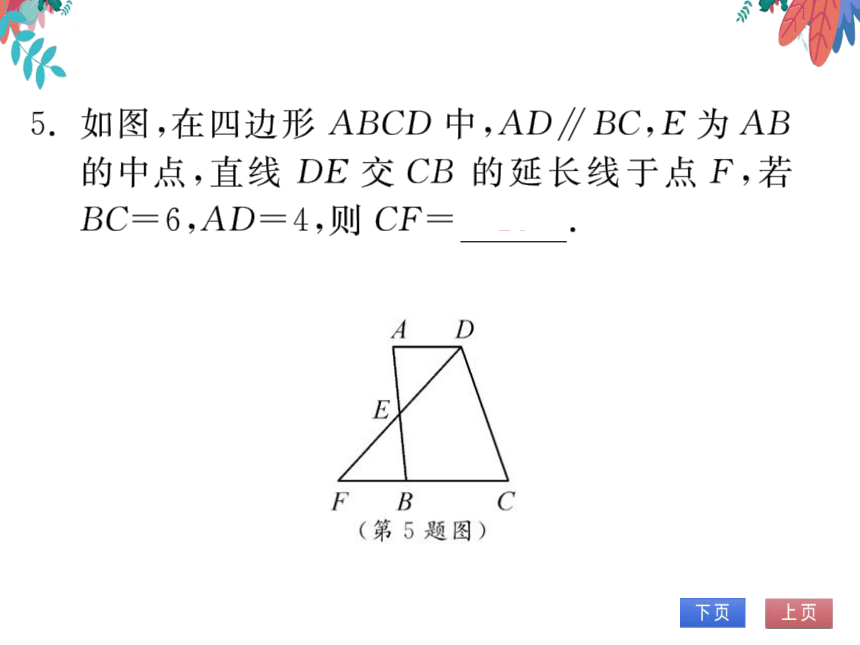
(第5题图)
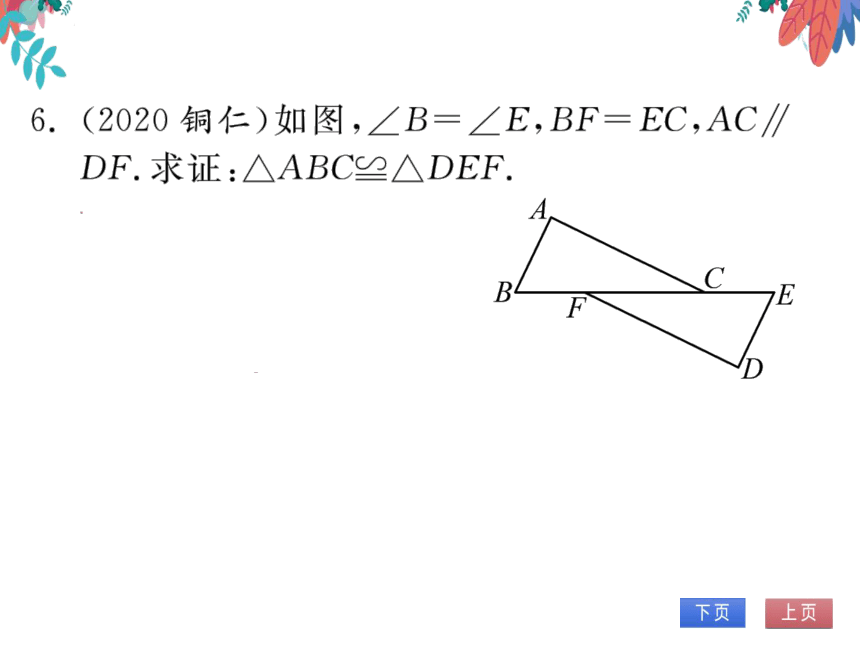
6.(2020铜仨)如图,∠B=∠E,BF=EC,AC∥
DF.求证:△ABC≌△DEF
证明:AC∥DF,
∠ACB=∠DFE.
BF=CE
BC=EF
∠B=∠E
在△ABC和△DEF中,BC=EF,
∠ACB=∠DFE,
△ABC≌△DEF(ASA)
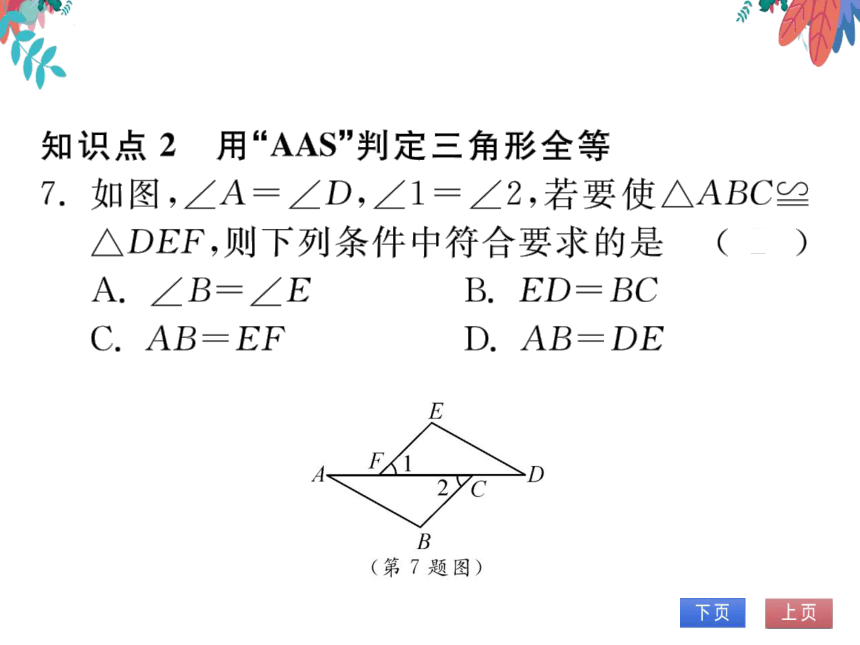
知识点2用“AAS”判定三角形全等
如图,∠A=∠D,∠1=∠2,若要使△ABC
DEF,则下列条件中符合要求的是
A.∠B=∠E
B. ED= BC
C. AB=EF
D. AB=DE
F△yC
D
B
(第7题图)
8.如图,CD⊥AB于点D,BE⊥AC于点E,BE
和CD相交于点O,∠1=∠2,则图中全等
角形共有
A.1对B.2对C.3对D.4对
D人
E
B
(第8题图)
9.如图,AD=AB,∠C=∠E,∠CDE=55°,则
∠ABE的度数为125°
(第9题图)
(第10题图)
10.如图,∠B=∠DEF,AB=DE,要证明
ABC≌△DEF.
(1)若以“SAS”为依据,还需添加的条件为
BC=EF或BE=CF
(2)若以“ASA”为依据,还需添加的条件为
∠A=∠D
(3若以“AAS”为依据,还需添加的条件为
∠ACB=∠F
11.如图,在△ABC中,AD是△ABC的中线,分
别过点C,B作AD及其延长线的垂线CF,
BE,垂足分别为F,E.求证:BE=CF
证明:AD是△ABC的
中线,∴BD=CD
BE⊥AE,CF⊥AE
∴∠BED=∠CFD=90°.B<
在△BED和△CFD中
知识要点全练
夯奧基础
知识点1用“ASA”判定三角形全等
1.如图,线段AD,BC相交于点O,若OA=OB,
为了用“ASA”判定△AOC≌△BOD,则应补
充的条件是
(A)
A.∠A=∠B
B. AD=BC
C. AC=BD
D. OC=OD
B
(第1题图)
2.如图,AB=AC,∠B=∠C,BE,CD相交于点
O,则直接判定△ABE≌△ACD的依据是
A. SAs
B. ASA
C. SSa
D. AAA
3.如图,某同学不小心把一块三角形玻璃打碎成
块,现在要到玻璃店配一块与原来完全相同
的玻璃,最省事的方法是
A.带①和②去
B.只带②去
C.只带③去
D.都带去
4.如图,直线l过正方形ABCD的顶点B,点A,
C到直线l的距离分别是AE=1,CF=2,则
EF的长是3
(第4题图)
(第5题图)
6.(2020铜仨)如图,∠B=∠E,BF=EC,AC∥
DF.求证:△ABC≌△DEF
证明:AC∥DF,
∠ACB=∠DFE.
BF=CE
BC=EF
∠B=∠E
在△ABC和△DEF中,BC=EF,
∠ACB=∠DFE,
△ABC≌△DEF(ASA)
知识点2用“AAS”判定三角形全等
如图,∠A=∠D,∠1=∠2,若要使△ABC
DEF,则下列条件中符合要求的是
A.∠B=∠E
B. ED= BC
C. AB=EF
D. AB=DE
F△yC
D
B
(第7题图)
8.如图,CD⊥AB于点D,BE⊥AC于点E,BE
和CD相交于点O,∠1=∠2,则图中全等
角形共有
A.1对B.2对C.3对D.4对
D人
E
B
(第8题图)
9.如图,AD=AB,∠C=∠E,∠CDE=55°,则
∠ABE的度数为125°
(第9题图)
(第10题图)
10.如图,∠B=∠DEF,AB=DE,要证明
ABC≌△DEF.
(1)若以“SAS”为依据,还需添加的条件为
BC=EF或BE=CF
(2)若以“ASA”为依据,还需添加的条件为
∠A=∠D
(3若以“AAS”为依据,还需添加的条件为
∠ACB=∠F
11.如图,在△ABC中,AD是△ABC的中线,分
别过点C,B作AD及其延长线的垂线CF,
BE,垂足分别为F,E.求证:BE=CF
证明:AD是△ABC的
中线,∴BD=CD
BE⊥AE,CF⊥AE
∴∠BED=∠CFD=90°.B<
在△BED和△CFD中
