12.2第4课时用“HL”证两个直角三角形全等 习题课件
文档属性
| 名称 | 12.2第4课时用“HL”证两个直角三角形全等 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:17:17 | ||
图片预览




文档简介
(共28张PPT)
知识要点全练
夯臭基础
知识点1用“HL"判定直角三角形全等
1.如图,OD⊥AB于点D,OE
AC于点E,且OD=OE,则
△AOD9△AOE的理由是
A. SS B. ASA C SSA D. HI
2.下列命题:①两直角边分别相等的两个直角
角形全等;②两锐角分别相等的两个直角三角
形全等;③斜边和一直角边分别相等的两个直
角三角形全等;④一锐角和一直角边分别相等
的两个直角三角形全等;⑤一锐角和斜边分别
相等的两个直角三角形全等.其中,正确的命
题有①③④⑤(填序号).
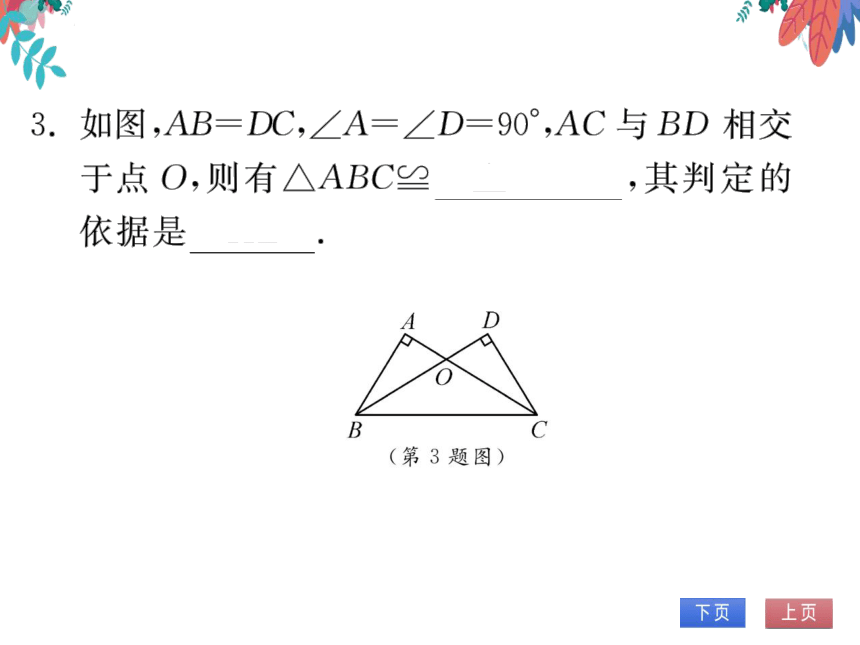
3.如图,AB=DC,∠A=∠D=90°,AC与BD相交
于点O,则有△ABC≌△DCB,其判定的
依据是HL
(第3题图)
(第4题图)
B
B D C
(第3题图)
(第4题图)
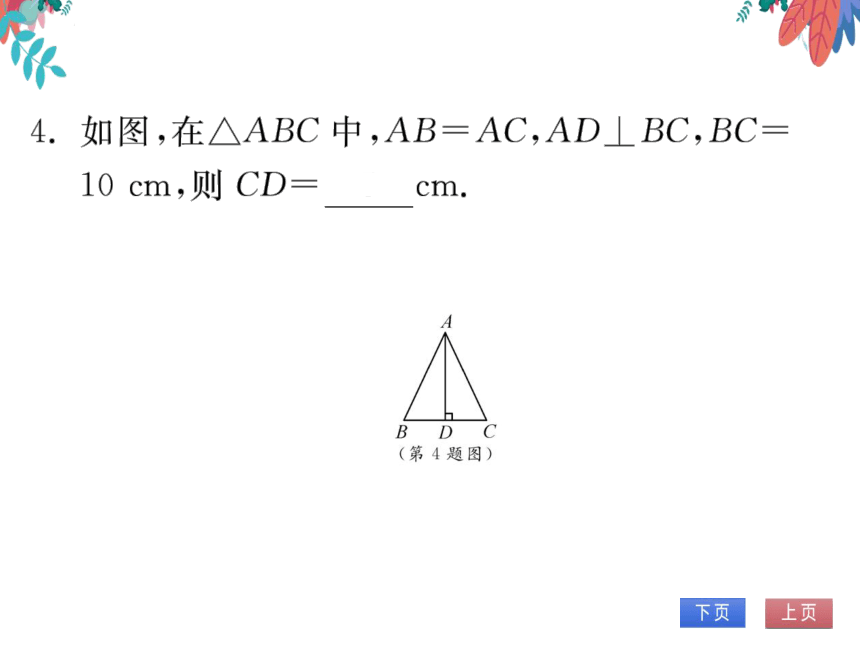
4.如图,在△ABC中,AB=AC,AD⊥BC,BC
10cm,则CD=5
cm
5.(教材P43练习T1变式)如图,小明和小芳以
相同的速度分别同时从A,B出发,小明沿AC
行走,小芳沿BD行走,并同时到达C,D.若
CB⊥AB,DA⊥AB,则CB与DA相等吗 为
什么
解:CB=DA
理由:由题意易知AC=BD
∴CB⊥AB,DA⊥AB,
∠DAB=∠CBA=90
在Rt△DAB和Rt△CBA中,
5.(教材P43练习T1变式)如图,小明和小芳以
相同的速度分别同时从A,B出发,小明沿AC
行走,小芳沿BD行走,并同时到达C,D.若
CB⊥AB,DA⊥AB,则CB与DA相等吗 为
什么
BD=AC
AB-BA
∴Rt△DAB≌Rt△CBA(HL)
DA=CB
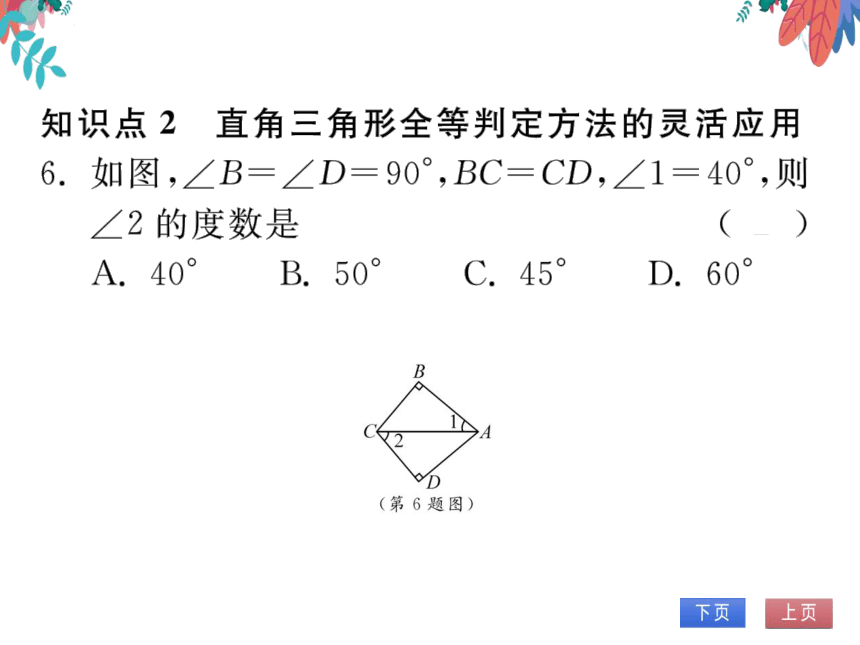
知识点2直角三角形全等判定方法的灵活应用
6.如图,∠B=∠D=90°,BC=CD,∠1=40°,则
∠2的度数是
(B)
A.40
B.50°
C.45
).60
(第6题图)
(第7题图)
(第8题图)
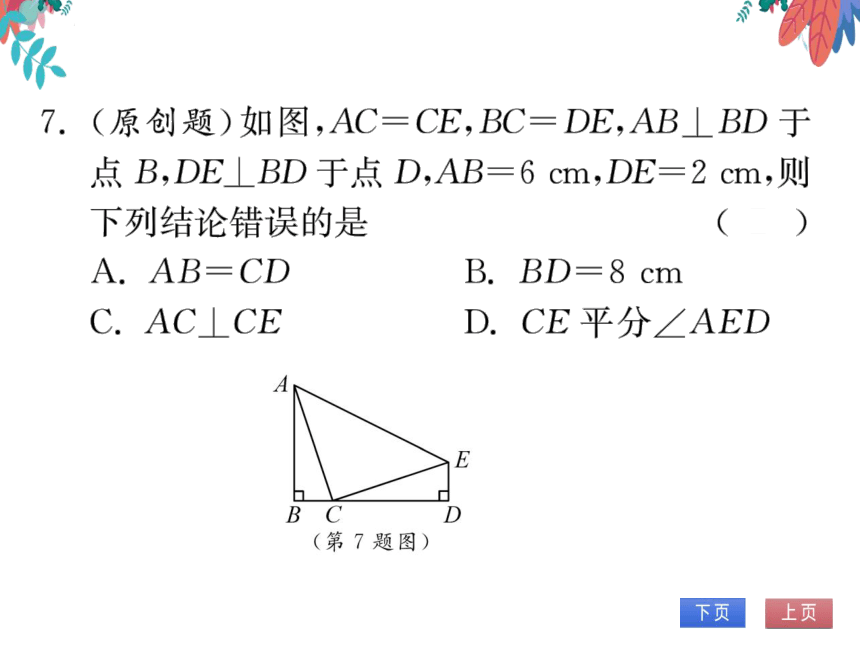
(原创题)如图,AC=CE,BC=DE,AB⊥BD于
点B,DE⊥BD于点D,AB=6cm,DE=2cm,则
下列结论错误的是
A.AB=CD
B. bd 8 cm
C. ACI CE
D.CE平分∠AED
B
E
E
B c
D A
B
(第6题图)
(第7题图)
第8题图)
8.如图,在四边形ABCD中,AD=CB,DE⊥AC
于点E,BF⊥AC于点F,且DE=BF,则图中
全等三角形有
A.1对B.2对C.3对D.4对
知识要点全练
夯臭基础
知识点1用“HL"判定直角三角形全等
1.如图,OD⊥AB于点D,OE
AC于点E,且OD=OE,则
△AOD9△AOE的理由是
A. SS B. ASA C SSA D. HI
2.下列命题:①两直角边分别相等的两个直角
角形全等;②两锐角分别相等的两个直角三角
形全等;③斜边和一直角边分别相等的两个直
角三角形全等;④一锐角和一直角边分别相等
的两个直角三角形全等;⑤一锐角和斜边分别
相等的两个直角三角形全等.其中,正确的命
题有①③④⑤(填序号).
3.如图,AB=DC,∠A=∠D=90°,AC与BD相交
于点O,则有△ABC≌△DCB,其判定的
依据是HL
(第3题图)
(第4题图)
B
B D C
(第3题图)
(第4题图)
4.如图,在△ABC中,AB=AC,AD⊥BC,BC
10cm,则CD=5
cm
5.(教材P43练习T1变式)如图,小明和小芳以
相同的速度分别同时从A,B出发,小明沿AC
行走,小芳沿BD行走,并同时到达C,D.若
CB⊥AB,DA⊥AB,则CB与DA相等吗 为
什么
解:CB=DA
理由:由题意易知AC=BD
∴CB⊥AB,DA⊥AB,
∠DAB=∠CBA=90
在Rt△DAB和Rt△CBA中,
5.(教材P43练习T1变式)如图,小明和小芳以
相同的速度分别同时从A,B出发,小明沿AC
行走,小芳沿BD行走,并同时到达C,D.若
CB⊥AB,DA⊥AB,则CB与DA相等吗 为
什么
BD=AC
AB-BA
∴Rt△DAB≌Rt△CBA(HL)
DA=CB
知识点2直角三角形全等判定方法的灵活应用
6.如图,∠B=∠D=90°,BC=CD,∠1=40°,则
∠2的度数是
(B)
A.40
B.50°
C.45
).60
(第6题图)
(第7题图)
(第8题图)
(原创题)如图,AC=CE,BC=DE,AB⊥BD于
点B,DE⊥BD于点D,AB=6cm,DE=2cm,则
下列结论错误的是
A.AB=CD
B. bd 8 cm
C. ACI CE
D.CE平分∠AED
B
E
E
B c
D A
B
(第6题图)
(第7题图)
第8题图)
8.如图,在四边形ABCD中,AD=CB,DE⊥AC
于点E,BF⊥AC于点F,且DE=BF,则图中
全等三角形有
A.1对B.2对C.3对D.4对
