13.1.2第1课时线段的垂直平分线的性质与判定 习题课件
文档属性
| 名称 | 13.1.2第1课时线段的垂直平分线的性质与判定 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:17:17 | ||
图片预览



文档简介
(共27张PPT)
知识要点全练
夯臭基础
知识点1线段的垂直平分线的性质
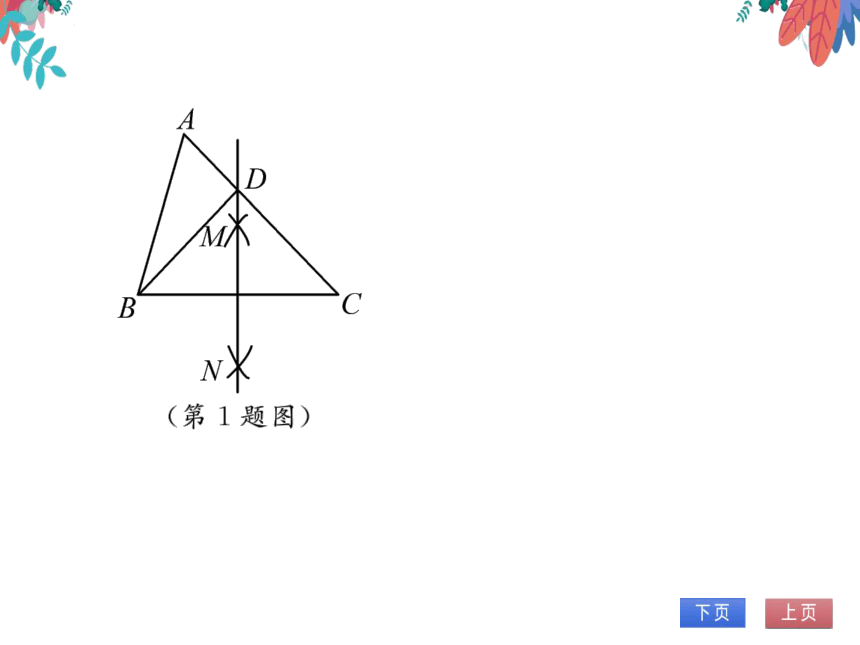
(2020成都)如图,在△ABC中,按以下步骤作
图:①分别以点B和C为圆心,以大于。BC
的长为半径作弧,两弧相交于点M和N;②作
直线MN交AC于点D,连接BD.若AC=6
AD=2,则BD的长为
C.4
D.6
(第1题图)
(第2题图)
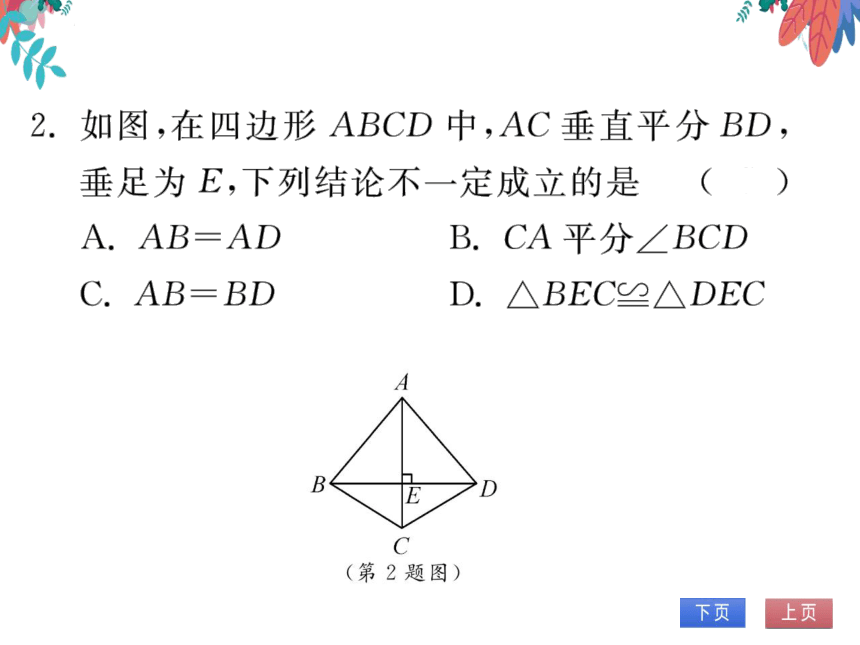
2.如图,在四边形ABCD中,AC垂直平分BD,
垂足为E,下列结论不一定成立的是(C
A. AB=AD
B.CA平分∠BCD
C.AB=BD
D.△BEC≌△DEC
B
D
(第2题图)
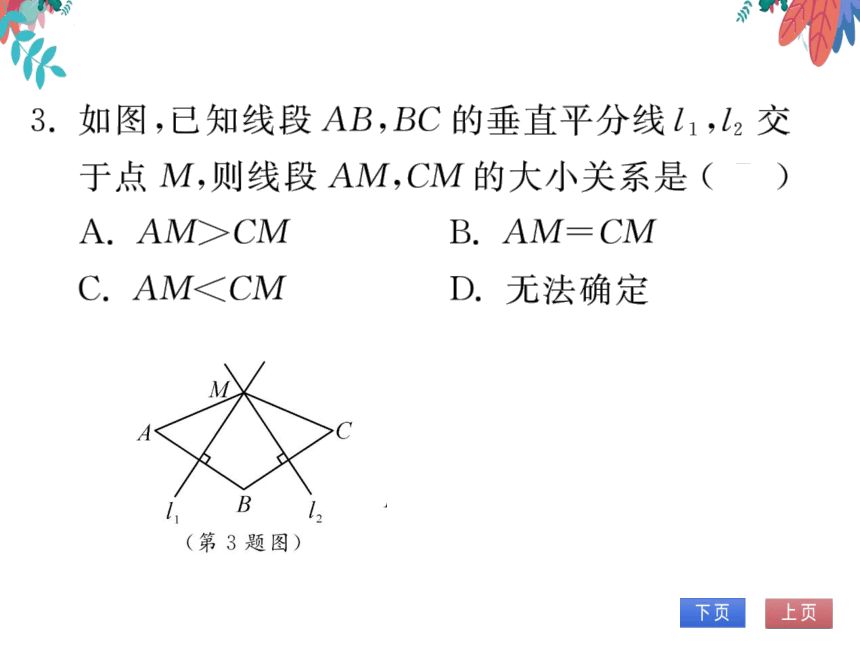
3.如图,已知线段AB,BC的垂直平分线l1,l2交
于点M,则线段AM,CM的大小关系是(B
A AMCM
B. AM=CM
C. AM CM
D.无法确定
(第3题图)
(第4题图)
M
B
B
D
C
B
第3题图)
(第4题图)
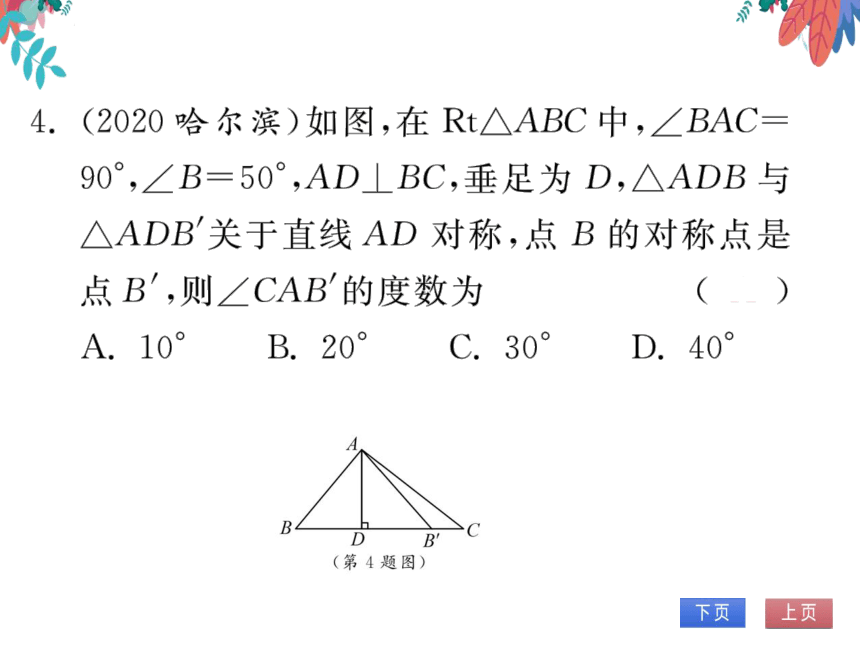
4.(2020哈尔滨)如图,在Rt△ABC中,∠BAC
90°,∠B=50°,AD⊥BC,垂足为D,△ADB与
△ADB关于直线AD对称,点B的对称点是
点B′,则∠CAB的度数为
A.10°
B.20°
C.30°
D.40°
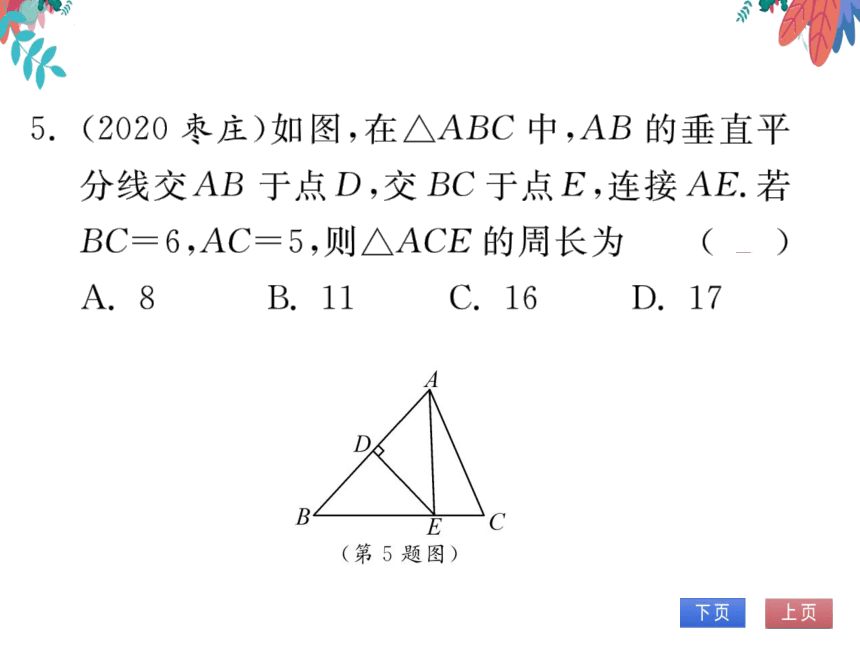
5.(2020枣庄)如图,在△ABC中,AB的垂直平
分线交AB于点D,交BC于点E,连接AE.若
BC=6,AC=5,则△ACE的周长为(B
A.8
B.11
C.16
D.17
B
(第5题图)
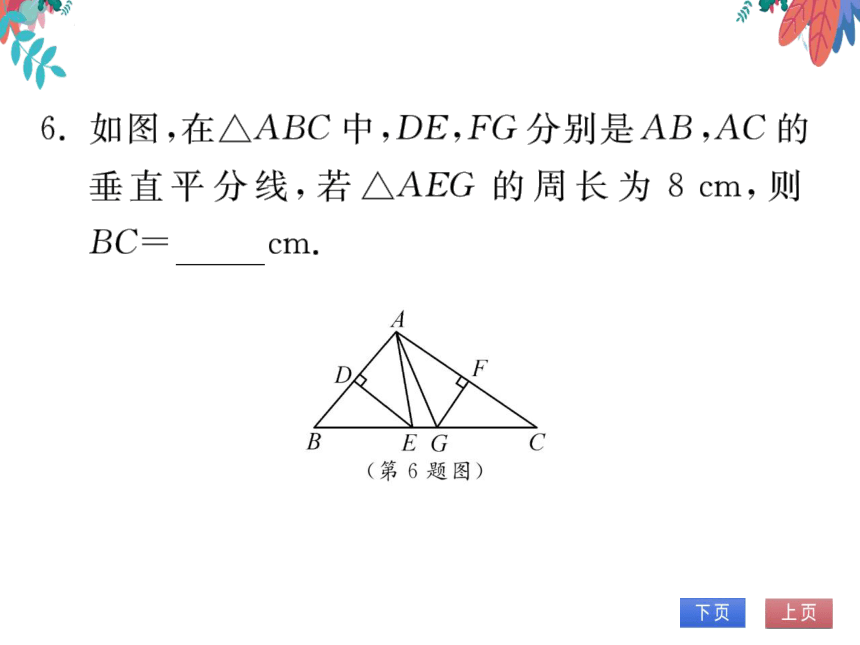
6.如图,在△ABC中,DE,FG分别是AB,AC的
垂直平分线,若△AEG的周长为8cm,则
bc
cm
B
E G
(第6题图)
知识点2线段的垂直平分线的判定
如图,AC=BC,AD=BD,则有
A.AB垂直平分CD
B.CD垂直平分AB
C.AB与CD互相平分
D.AB平分∠CAD
8.点P是锐角△ABC内一点,且PA=PB
PC,则点P是△ABC
A.三条角平分线的交点
B.三条中线的交点
条高的交点
D.三边垂直平分线的交点
9.如图,在△ABC中,AB=AC,O是△ABC内
点,且OB=OC求证:AO垂直平分BC
证明:∵AB=AC
点A在BC的垂直平分线上
OB=OC
点O也在BC的垂直平分线上
AO垂直平分BC
知识点3利用尺规作已知直线的垂线
10.如图,已知钝角三角形ABC,其中∠A是钝
角,求作AC边上的高BH
解:如图,线段BH即为所求
规律方法全练
提升能力
11.如图,在△ABC中,AB=AC,AB的垂直平
分线ED交AC于点D,△ABC和△DBC的
周长分别是60cm和38cm,则△ABC的腰
长和底边长分别为
A.24cm和12cmB.16cm和22cm
C.20cm和16cmD.22cm和16cm
知识要点全练
夯臭基础
知识点1线段的垂直平分线的性质
(2020成都)如图,在△ABC中,按以下步骤作
图:①分别以点B和C为圆心,以大于。BC
的长为半径作弧,两弧相交于点M和N;②作
直线MN交AC于点D,连接BD.若AC=6
AD=2,则BD的长为
C.4
D.6
(第1题图)
(第2题图)
2.如图,在四边形ABCD中,AC垂直平分BD,
垂足为E,下列结论不一定成立的是(C
A. AB=AD
B.CA平分∠BCD
C.AB=BD
D.△BEC≌△DEC
B
D
(第2题图)
3.如图,已知线段AB,BC的垂直平分线l1,l2交
于点M,则线段AM,CM的大小关系是(B
A AMCM
B. AM=CM
C. AM CM
D.无法确定
(第3题图)
(第4题图)
M
B
B
D
C
B
第3题图)
(第4题图)
4.(2020哈尔滨)如图,在Rt△ABC中,∠BAC
90°,∠B=50°,AD⊥BC,垂足为D,△ADB与
△ADB关于直线AD对称,点B的对称点是
点B′,则∠CAB的度数为
A.10°
B.20°
C.30°
D.40°
5.(2020枣庄)如图,在△ABC中,AB的垂直平
分线交AB于点D,交BC于点E,连接AE.若
BC=6,AC=5,则△ACE的周长为(B
A.8
B.11
C.16
D.17
B
(第5题图)
6.如图,在△ABC中,DE,FG分别是AB,AC的
垂直平分线,若△AEG的周长为8cm,则
bc
cm
B
E G
(第6题图)
知识点2线段的垂直平分线的判定
如图,AC=BC,AD=BD,则有
A.AB垂直平分CD
B.CD垂直平分AB
C.AB与CD互相平分
D.AB平分∠CAD
8.点P是锐角△ABC内一点,且PA=PB
PC,则点P是△ABC
A.三条角平分线的交点
B.三条中线的交点
条高的交点
D.三边垂直平分线的交点
9.如图,在△ABC中,AB=AC,O是△ABC内
点,且OB=OC求证:AO垂直平分BC
证明:∵AB=AC
点A在BC的垂直平分线上
OB=OC
点O也在BC的垂直平分线上
AO垂直平分BC
知识点3利用尺规作已知直线的垂线
10.如图,已知钝角三角形ABC,其中∠A是钝
角,求作AC边上的高BH
解:如图,线段BH即为所求
规律方法全练
提升能力
11.如图,在△ABC中,AB=AC,AB的垂直平
分线ED交AC于点D,△ABC和△DBC的
周长分别是60cm和38cm,则△ABC的腰
长和底边长分别为
A.24cm和12cmB.16cm和22cm
C.20cm和16cmD.22cm和16cm
