13.3.2第1课时等边三角形的性质与判定 习题课件
文档属性
| 名称 | 13.3.2第1课时等边三角形的性质与判定 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:17:17 | ||
图片预览








文档简介
(共25张PPT)
知识要点全练
夯奥基础
知识点1等边三角形的性质
1.如图,在等边三角形ABC中
AD⊥BC,垂足为D,点E在线
段AD上,∠EBC=45°,贝
∠ACE等于
A.15°
B.30
C.45°
D.60°
如图,张等边三角形的纸片,剪去一个角后得
到一个四边形,则图中∠a+∠的度数是(C)
A.180°B.220°C.240°D.300°
(第2题图)
第3题图)
D
B
E
(第2题图)
(第3题图)
3.如图,已知△ABC为等边三角形,BD为中线,
延长BC至点E,使CE=CD,连接DE,若
BD=3,则DE
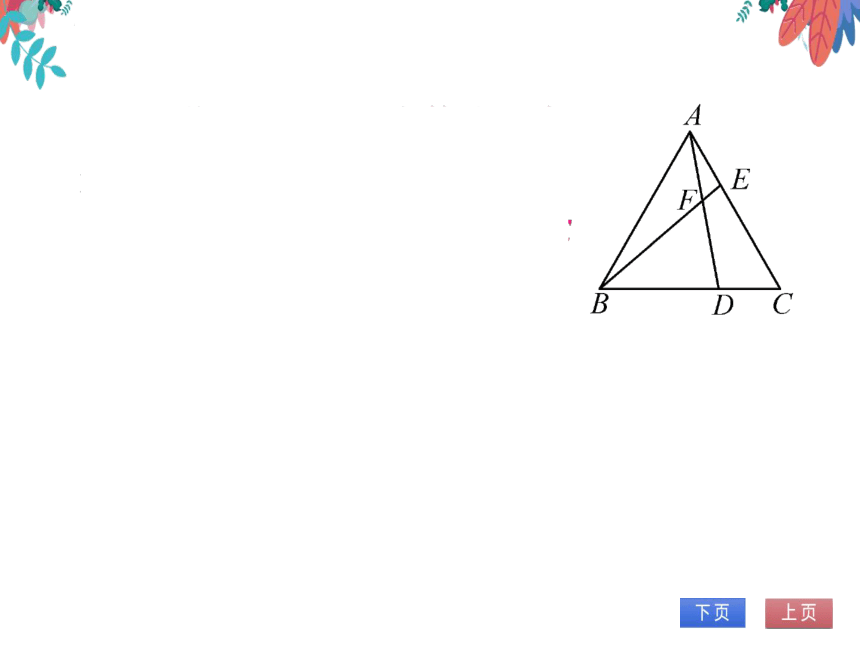
4.如图,已知△ABC为等边三角形,点D,E分
别在BC,AC边上,AE=CD,AD与BE相交
于点F.
(1)求证:△ABE≌△CAD
(2)求∠AFB的度数
(1)证明
ABC为等边三角
形,∴∠BAC=∠ABC=∠C
60°,AB=AC=BC.在△ABE
AB=CA
和△CAD中,∠BAC=∠C,
AECD
△ABE≌△CAD(SAS)
(2)解:∴△ABE≌△CAD
∠ABE=∠CAD
又∵∠AFE=∠ABE+∠BAD,
∠AFE=∠BAD+∠CAD=∠BAC=60°
∠AFB=180-∠AFE=120
知识点2等边三角形的判定
5.在△ABC中:①若AB=BC=CA,则△ABC为
等边三角形;②若∠A=∠B=∠C,则△ABC
为等边三角形;③有两个角都是60°的三角形是
等边三角形;④有一个角为60°的等腰三角形是
等边三角形.上述结论中正确的有
A.1个B.2个C.3个D.4个
6.如图,在△ABC中,∠ACB=120°,CD平分
∠ACB,AE∥DC,交BC的延长线于点E,试
证明△ACE是等边三角形
证明:如图,CD平分∠ACB,
∠ACB=120°,
∠1=∠21
120=60,B
14
E
AE∥D
∠3=∠4=∠E=60°1=60
∠3=∠2=60°,∠E=∠
ACE是等边三角形
如图,在△ABC中,AB=AC,D为AC的中
点,DE⊥AB,DF⊥BC,垂足分别为E,F,且
DE=DF.求证:△ABC是等边三角形
证明:AB=AC
∠B=∠C
∴DE⊥AB,DF⊥BC
∠DEA=∠DFC=90°
D为AC的中点,
DA=DC
又∵DE=DF,
Rt△ADE≌Rt△CDF(HL
∠A=∠C.∴∠A=∠B=∠C.
△ABC是等边三角形
知识要点全练
夯奥基础
知识点1等边三角形的性质
1.如图,在等边三角形ABC中
AD⊥BC,垂足为D,点E在线
段AD上,∠EBC=45°,贝
∠ACE等于
A.15°
B.30
C.45°
D.60°
如图,张等边三角形的纸片,剪去一个角后得
到一个四边形,则图中∠a+∠的度数是(C)
A.180°B.220°C.240°D.300°
(第2题图)
第3题图)
D
B
E
(第2题图)
(第3题图)
3.如图,已知△ABC为等边三角形,BD为中线,
延长BC至点E,使CE=CD,连接DE,若
BD=3,则DE
4.如图,已知△ABC为等边三角形,点D,E分
别在BC,AC边上,AE=CD,AD与BE相交
于点F.
(1)求证:△ABE≌△CAD
(2)求∠AFB的度数
(1)证明
ABC为等边三角
形,∴∠BAC=∠ABC=∠C
60°,AB=AC=BC.在△ABE
AB=CA
和△CAD中,∠BAC=∠C,
AECD
△ABE≌△CAD(SAS)
(2)解:∴△ABE≌△CAD
∠ABE=∠CAD
又∵∠AFE=∠ABE+∠BAD,
∠AFE=∠BAD+∠CAD=∠BAC=60°
∠AFB=180-∠AFE=120
知识点2等边三角形的判定
5.在△ABC中:①若AB=BC=CA,则△ABC为
等边三角形;②若∠A=∠B=∠C,则△ABC
为等边三角形;③有两个角都是60°的三角形是
等边三角形;④有一个角为60°的等腰三角形是
等边三角形.上述结论中正确的有
A.1个B.2个C.3个D.4个
6.如图,在△ABC中,∠ACB=120°,CD平分
∠ACB,AE∥DC,交BC的延长线于点E,试
证明△ACE是等边三角形
证明:如图,CD平分∠ACB,
∠ACB=120°,
∠1=∠21
120=60,B
14
E
AE∥D
∠3=∠4=∠E=60°1=60
∠3=∠2=60°,∠E=∠
ACE是等边三角形
如图,在△ABC中,AB=AC,D为AC的中
点,DE⊥AB,DF⊥BC,垂足分别为E,F,且
DE=DF.求证:△ABC是等边三角形
证明:AB=AC
∠B=∠C
∴DE⊥AB,DF⊥BC
∠DEA=∠DFC=90°
D为AC的中点,
DA=DC
又∵DE=DF,
Rt△ADE≌Rt△CDF(HL
∠A=∠C.∴∠A=∠B=∠C.
△ABC是等边三角形
