14.2.1平方差公式 习题课件
图片预览






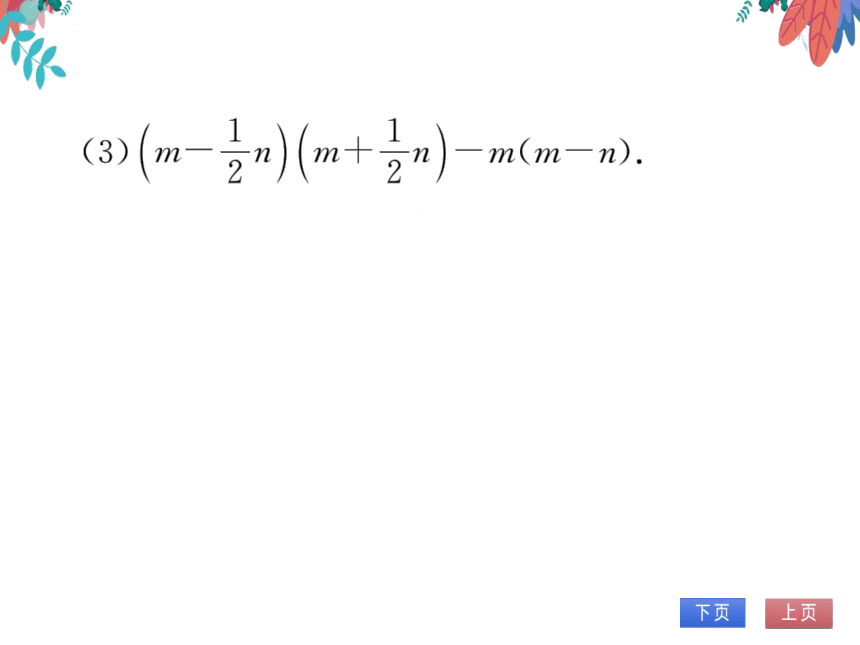
文档简介
(共28张PPT)
标题截图放置居中位置
知识要点全练
夯基础
知识点1平方差公式
1.计算(4x+1)(4x-1)的结果为
A.16x2-1
B.-16x2-1
C.4x2-1
D.4x2+1
2.计算(x-y)(-y-x)的结果是
A
4.填
(1)(2x-3y)
2x+3y)=4,x2-9y2;
(2)(
+n)
5.计算:
(1)(xy+5)(xy-5)
解:原式=(xy)2-52=x2y2-2
(2)(-4a+3)(-4a-3);
解:原式=(-4a)2-32=16a2-9
72
m(n
解:原式=m
72
m2tmn
2n2
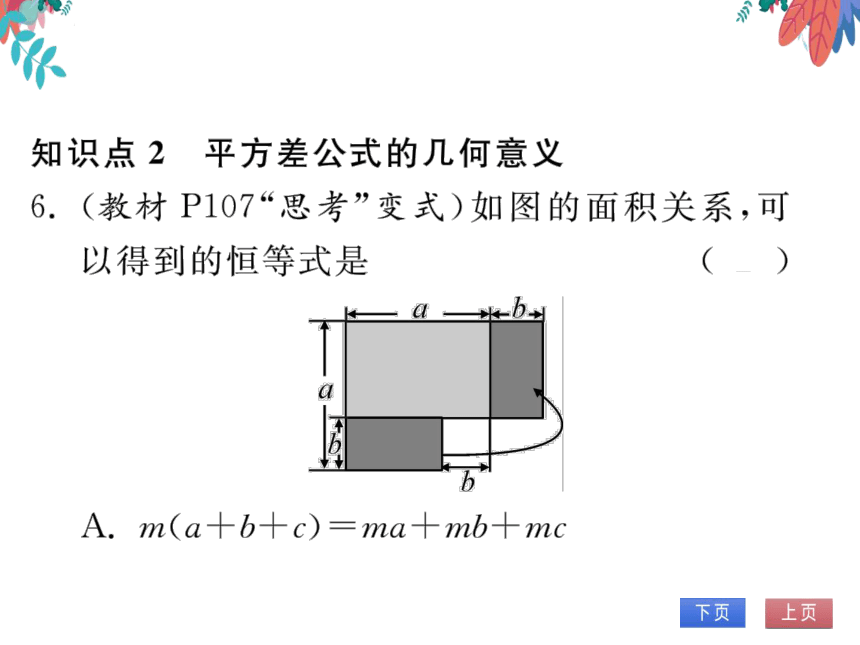
知识点2平方差公式的几何意义
6.(教材P107“思考”变式)如图的面积关系,可
以得到的恒等式是
A. m(a+6+c)=ma++mc
B.(a+b)(a-b)=a2-b2
c. ( a-b
abb
D. (a+b)
2ab+b2
7.如图①,把一张长方形纸片沿着线段AB剪
开,把剪成的两张纸片拼成如图②所示的
图形
b
(1)设图①中阴影部分面积为S1,图②中阴影
部分面积为S2,请直接用含a,b的式子表
示S1,S2
(2)请写出上述过程所揭示的乘法公式
解:(1)S1=(a+b)(a-b),S2=a2-b2
(2)(a+b)(a-b)=a2-b2
知识点3平方差公式的运用
8.运用平方差公式简便计算
(1)9.8×10.2
解:原式=(10-0.2)×(10+0.2)
102-0.22
99.96.
(2)1007×993;
解:原式=(1000+7)×(1000-7)
10002-7
999951
(3)129×127—1282
解:原式=(128+1)×(128-1)-1282
1282-1-128
规律方法全练
提升能力
若M·(2x-y2)=y1-4x2,则多项式M应为
2. x
B
2+2
c. 2.x
C
10.计算(x4+1)(x2+1)(x+1)(x-1)的结果是
B.
C.(x+1)
11.下列计算正确的是
A.(a+3b)(a-3b)
36
3b)(a-3b)
96
3b)(a-3b)
96
D.(-a-3b)(a+3b)
96
12.对于任意正整数n,能整除式子(3n
1)(3n-1)-(3-n)(3+n)的整数是((
A.3
C.10
D.9
13.若
且
n-=2,则3m+3
14.若(a+b+2)(a+b-2)=32,则a+b
士6
标题截图放置居中位置
知识要点全练
夯基础
知识点1平方差公式
1.计算(4x+1)(4x-1)的结果为
A.16x2-1
B.-16x2-1
C.4x2-1
D.4x2+1
2.计算(x-y)(-y-x)的结果是
A
4.填
(1)(2x-3y)
2x+3y)=4,x2-9y2;
(2)(
+n)
5.计算:
(1)(xy+5)(xy-5)
解:原式=(xy)2-52=x2y2-2
(2)(-4a+3)(-4a-3);
解:原式=(-4a)2-32=16a2-9
72
m(n
解:原式=m
72
m2tmn
2n2
知识点2平方差公式的几何意义
6.(教材P107“思考”变式)如图的面积关系,可
以得到的恒等式是
A. m(a+6+c)=ma++mc
B.(a+b)(a-b)=a2-b2
c. ( a-b
abb
D. (a+b)
2ab+b2
7.如图①,把一张长方形纸片沿着线段AB剪
开,把剪成的两张纸片拼成如图②所示的
图形
b
(1)设图①中阴影部分面积为S1,图②中阴影
部分面积为S2,请直接用含a,b的式子表
示S1,S2
(2)请写出上述过程所揭示的乘法公式
解:(1)S1=(a+b)(a-b),S2=a2-b2
(2)(a+b)(a-b)=a2-b2
知识点3平方差公式的运用
8.运用平方差公式简便计算
(1)9.8×10.2
解:原式=(10-0.2)×(10+0.2)
102-0.22
99.96.
(2)1007×993;
解:原式=(1000+7)×(1000-7)
10002-7
999951
(3)129×127—1282
解:原式=(128+1)×(128-1)-1282
1282-1-128
规律方法全练
提升能力
若M·(2x-y2)=y1-4x2,则多项式M应为
2. x
B
2+2
c. 2.x
C
10.计算(x4+1)(x2+1)(x+1)(x-1)的结果是
B.
C.(x+1)
11.下列计算正确的是
A.(a+3b)(a-3b)
36
3b)(a-3b)
96
3b)(a-3b)
96
D.(-a-3b)(a+3b)
96
12.对于任意正整数n,能整除式子(3n
1)(3n-1)-(3-n)(3+n)的整数是((
A.3
C.10
D.9
13.若
且
n-=2,则3m+3
14.若(a+b+2)(a+b-2)=32,则a+b
士6
