14.2.2第1课时完全平方公式 习题课件
文档属性
| 名称 | 14.2.2第1课时完全平方公式 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 00:00:00 | ||
图片预览








文档简介
(共28张PPT)
标题截图放置居中位置
知识要点全练
夯臭基础
知识点1完全平方公式
(2020黔东南)下列运算正确的是
4
fIy
D.(-3x)2=9x2
2.下列运算结果是9x2-6x+1的是
A.(3x+1)2
B.(3x-1)
D.一(3x+1)2
3.下列计算正确的是
A. (x+y
y
C
C.(x+1)(x-1)
D.(x-1)2=x2-1
若x2+2(m-3)x+16是关于x的完全平方
式,则m=7或-1
5.(原创题)若(2-x)=m2-4x+x,则m=±2
6.计算:
(1)(3a+2b)2;
解:原式=9a2+12ab+4b2
(2)(5-ab)
解:原式=a2b2-10ab+25
(3)(-2xy-1)2
解:原式=4x2y2+4xy+1
知识点2完全平方公式的几何意义
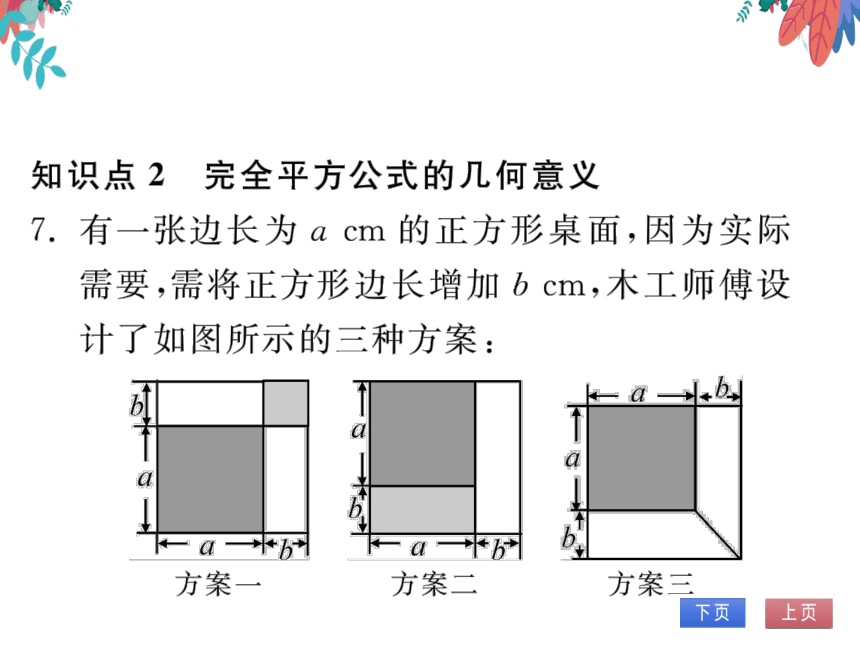
有一张边长为acm的正方形桌面,因为实际
需要,需将正方形边长增加bcm,木工师傅设
计了如图所示的三种方案:
b
b
b
b
方案
方案
方案
小明发现这三种方案都能验证公式:a2+2ab
b2=(a+b)
对于方案一,小明是这样验证的:
6ab+b2
2ab+b2=(a+b)
请你根据方案二、方案三,写出公式的验证过程
解:方案二:a2+ab+(a+b)b=a2+ab+ab+
b2=a2+2ab+b2=(a+b)2
方案三:a2+
a+(a+b)]b[
+a+(a+b)1b
212
a2+ab+b2ab+b2=a2+2ab+62=(a+6)2
知识点3完全平方公式的运用
8.运用完全平方公式计算9.82,最合适的方法是
A.(9+0.8)
B.(10-0.2)2
C.(9.7+0.1)2
D.(9.9—0.1)
9.如图,从边长为(a+1)cm的正方形纸片中剪
去一个边长为(a-1)cm的正方形(a>1),剩
余部分沿虚线剪拼成一个长方形(不重叠、无
缝隙),则该长方形的面积是
A.2 cm2
b. 2a cm
a cm
D.(a2-1)cm
10.运用完全平方公式简便计算:
(1)1022;
解:原式=(100+2)2
10000+400+4
10404
(2)(原创题)(5952)
解:原式=(60
60
3600
2+1
3600
3598
3600
规律方法全练
提升能力
11.已知(m-n)2=8,(m+n)2=2,则
的
值为
A.10
标题截图放置居中位置
知识要点全练
夯臭基础
知识点1完全平方公式
(2020黔东南)下列运算正确的是
4
fIy
D.(-3x)2=9x2
2.下列运算结果是9x2-6x+1的是
A.(3x+1)2
B.(3x-1)
D.一(3x+1)2
3.下列计算正确的是
A. (x+y
y
C
C.(x+1)(x-1)
D.(x-1)2=x2-1
若x2+2(m-3)x+16是关于x的完全平方
式,则m=7或-1
5.(原创题)若(2-x)=m2-4x+x,则m=±2
6.计算:
(1)(3a+2b)2;
解:原式=9a2+12ab+4b2
(2)(5-ab)
解:原式=a2b2-10ab+25
(3)(-2xy-1)2
解:原式=4x2y2+4xy+1
知识点2完全平方公式的几何意义
有一张边长为acm的正方形桌面,因为实际
需要,需将正方形边长增加bcm,木工师傅设
计了如图所示的三种方案:
b
b
b
b
方案
方案
方案
小明发现这三种方案都能验证公式:a2+2ab
b2=(a+b)
对于方案一,小明是这样验证的:
6ab+b2
2ab+b2=(a+b)
请你根据方案二、方案三,写出公式的验证过程
解:方案二:a2+ab+(a+b)b=a2+ab+ab+
b2=a2+2ab+b2=(a+b)2
方案三:a2+
a+(a+b)]b[
+a+(a+b)1b
212
a2+ab+b2ab+b2=a2+2ab+62=(a+6)2
知识点3完全平方公式的运用
8.运用完全平方公式计算9.82,最合适的方法是
A.(9+0.8)
B.(10-0.2)2
C.(9.7+0.1)2
D.(9.9—0.1)
9.如图,从边长为(a+1)cm的正方形纸片中剪
去一个边长为(a-1)cm的正方形(a>1),剩
余部分沿虚线剪拼成一个长方形(不重叠、无
缝隙),则该长方形的面积是
A.2 cm2
b. 2a cm
a cm
D.(a2-1)cm
10.运用完全平方公式简便计算:
(1)1022;
解:原式=(100+2)2
10000+400+4
10404
(2)(原创题)(5952)
解:原式=(60
60
3600
2+1
3600
3598
3600
规律方法全练
提升能力
11.已知(m-n)2=8,(m+n)2=2,则
的
值为
A.10
