15.1.1从分数到分式 习题课件
图片预览








文档简介
(共24张PPT)
知识要点全练
夯奧基础
知识点1分式的概念
1 a
a+b 2
1.下列式子:2a
T
其中分式有
A.1个
B.2个
C.3个
D.4个
2.面积为4m2的长方形的一边长为am,则另
边长为
(B)
A.4
Ba m
4
3.列式表示下列各量:
(1)王老师骑自行车用了mh到达距离家nkm的
学校,则王老师的平均速度是
m/h;若
Kr
王老师乘公共汽车可少用0.2h,则公共汽车
的平均速度是
m-0.2
Km/h
(2)某班在一次考试中,有m人得90分,有n
人得80分,那么这两部分人合在一起的平
均分是90+802分
72
72
知识点2分式有(无)意义的条件
若分式—在实数范围内有意义,则实数a的
取值范围为
4
B.a>4
C.a<4
D.a≠4
5.(2020安顺)当x=1时,下列分式没有意义的
是
x+1
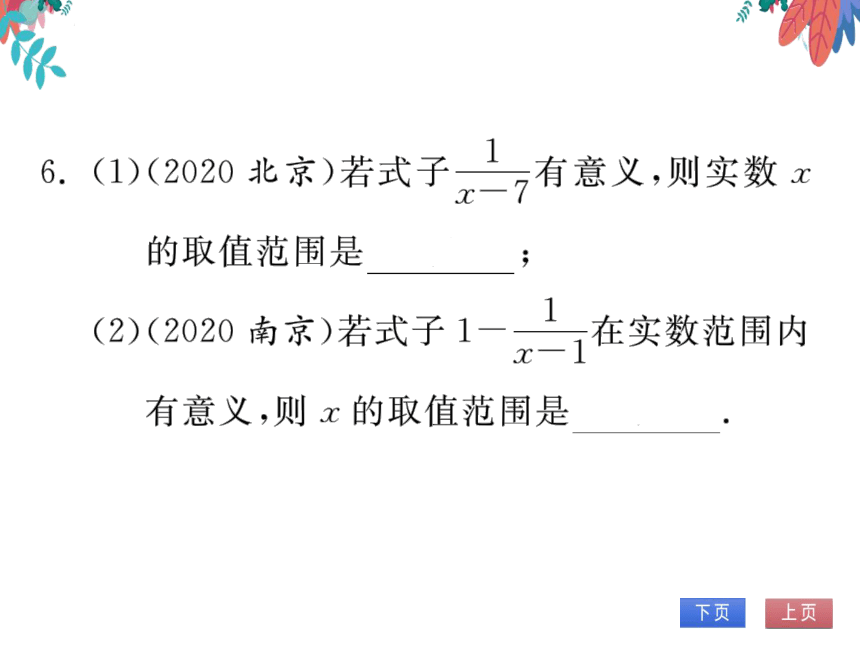
6.(1)(2020北京)若式子—有意义,则实数x
的取值范围是x≠7
(2)(2020南京)若式子
在实数范围内
有意义,则x的取值范围是x≠1
当x取何值时,下列分式有意义
x+3
x+7
(2)
(3)
2x-4
(x-2)(x+3)
解:(1)由题意知2x-4≠0,∴x≠2
(2)由题意知x取全体实数
(3)由题意知x-2≠0且x+3≠0,
x≠2且x≠-3
知识点3分式的值为0的条件
8.(2020丽水)分式。的值是零,则x的值为
若分式
的值为0,则x的值为(A)
10.已知分式2xm,当x=2时,分式的值为0
当x=1时,分式无意义,则m+n=3
11.利用下面三个整式中的两个或三个写出一个
分式,使得当x=5时,分式的值为0,且当
x=-6时,分式无意义
①x+5;②x-5;③x2-36
解:由题意可知该分式分子中一定含整式x
5,分母必含整式x2-36
故该分式可以是
(答案不唯一)
36
规律方法全练多
提升能力
12.下列式子:-3x
9
其
y
T
中是分式的有
A.2个B.3个C.4个D.5个
x+2
13.若
的值为正数,则x的取值范围为
2且x≠1D.x≠1
14.下列关于分式的判断,正确的是
A.当x=2时
的值为
B.当x≠5时
有意义
4
C.无论x为何值
的值不可能为整数
D.无论x为何值
的值总是正数
15.若分式
的值为负数,则x应满足(A)
B.x>—3
知识要点全练
夯奧基础
知识点1分式的概念
1 a
a+b 2
1.下列式子:2a
T
其中分式有
A.1个
B.2个
C.3个
D.4个
2.面积为4m2的长方形的一边长为am,则另
边长为
(B)
A.4
Ba m
4
3.列式表示下列各量:
(1)王老师骑自行车用了mh到达距离家nkm的
学校,则王老师的平均速度是
m/h;若
Kr
王老师乘公共汽车可少用0.2h,则公共汽车
的平均速度是
m-0.2
Km/h
(2)某班在一次考试中,有m人得90分,有n
人得80分,那么这两部分人合在一起的平
均分是90+802分
72
72
知识点2分式有(无)意义的条件
若分式—在实数范围内有意义,则实数a的
取值范围为
4
B.a>4
C.a<4
D.a≠4
5.(2020安顺)当x=1时,下列分式没有意义的
是
x+1
6.(1)(2020北京)若式子—有意义,则实数x
的取值范围是x≠7
(2)(2020南京)若式子
在实数范围内
有意义,则x的取值范围是x≠1
当x取何值时,下列分式有意义
x+3
x+7
(2)
(3)
2x-4
(x-2)(x+3)
解:(1)由题意知2x-4≠0,∴x≠2
(2)由题意知x取全体实数
(3)由题意知x-2≠0且x+3≠0,
x≠2且x≠-3
知识点3分式的值为0的条件
8.(2020丽水)分式。的值是零,则x的值为
若分式
的值为0,则x的值为(A)
10.已知分式2xm,当x=2时,分式的值为0
当x=1时,分式无意义,则m+n=3
11.利用下面三个整式中的两个或三个写出一个
分式,使得当x=5时,分式的值为0,且当
x=-6时,分式无意义
①x+5;②x-5;③x2-36
解:由题意可知该分式分子中一定含整式x
5,分母必含整式x2-36
故该分式可以是
(答案不唯一)
36
规律方法全练多
提升能力
12.下列式子:-3x
9
其
y
T
中是分式的有
A.2个B.3个C.4个D.5个
x+2
13.若
的值为正数,则x的取值范围为
2且x≠1D.x≠1
14.下列关于分式的判断,正确的是
A.当x=2时
的值为
B.当x≠5时
有意义
4
C.无论x为何值
的值不可能为整数
D.无论x为何值
的值总是正数
15.若分式
的值为负数,则x应满足(A)
B.x>—3
