15.3第一课时分式方程及其解法 习题课件
文档属性
| 名称 | 15.3第一课时分式方程及其解法 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:16:16 | ||
图片预览








文档简介
(共22张PPT)
标题截图放置居中位置
知识要点全练
夯奥基础
知识点1分式方程的概念
1.下列方程是分式方程的是
2x=5
1=0
x-2
4x=0
2.下列方程是关于x的分式方程的是(D
3+x
B
6
2 x
b
24x-5
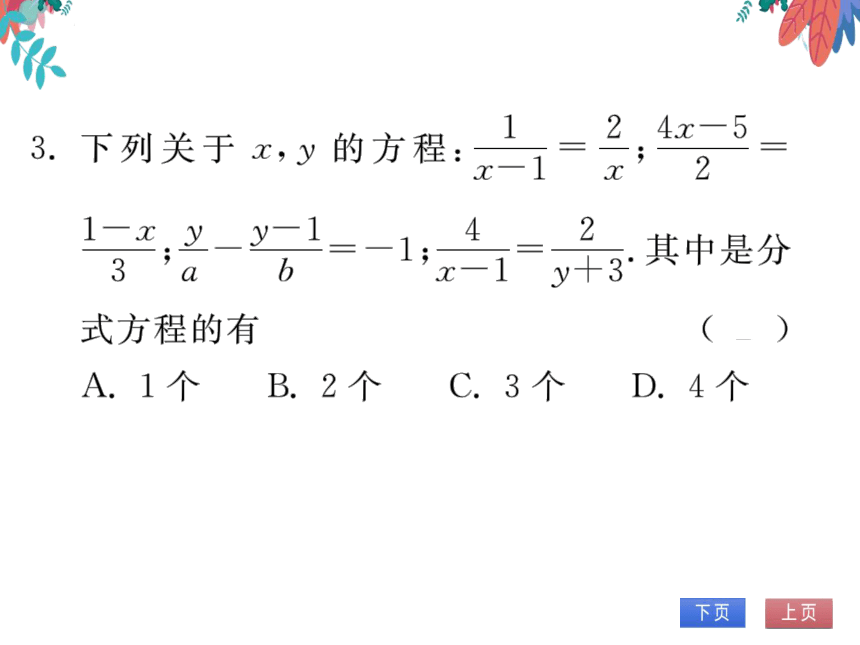
3.下列关于x,y的方程:
4
其中是分
b
式方程的有
(B)
A.1个B.2个C.3个D.4个
知识点2解分式方程
4.(2020哈尔滨)方程
的解为(D
B. x
259
大,x-3
(2020成都)已知x=2是分式方程
1的解,那么实数k的值为
D.6
x-1
6.若关于x的分式方程=无解,则m
的值为
(B)
(2020黑龙江)已知关于x的分式方程
k
4
的解为非正数,则k的取值范围是
A)
A.k≤-12
b.k
12
c.k
12
D.k<-12
若分式
与一的值相等,则x
x+2
9.(2020南京)方程
C
的解是x
1x+2
4
10.若2x-1=3(x-1)1,则x的值是2
11.若关于x的分式方程
ca
1的解为正数,则
x-1
的取值范围是a>1且a≠2
12.解方程:
x+1
4
(1)
x-1x2-1
解:方程两边同乘(x-1)(x+1),得
(x+1)2+4=(x-1)(x+1),∴x
检验:当x=-3时,(x-1)(x+1)≠0,
原方程的解是x
(2)
x2+3x
解:原方程可化为
x(x+3)x(x-1)
方程两边同乘x(x+3)(x-1),得
5(x-1)-(x+3)=0,∴x=2
检验:当x=2时,x(x+3)(x-1)≠0,
∴原方程的解是x=2
2 x
(3)
2(x-2)(x-3)
解:方程两边同乘(x-3)(x-2),得
a(
)=2x(x-2)
3x-1
2x2-4x
检验:当x=1时,(x-3)(x-2)≠0,
原方程的解为x=1
规律方法全练
提升能力
13.(2020齐齐哈尔)若关于x的分式方程
3.3
2
5的解为正数,则m的取值范
22—x
为
A.m<—10
B.m≤-10
C.m≥-10且m≠-6
D.m>-10且m≠-6
14.(2020重庆)若关于x的一元一次不等式组
3x-1
的解集为x≤a,且关于y的
sa
4
分式方程
1有正整数解,则所
有满足条件的整数a的值之积是
a)
14C.2
56
15.(2020遂宁)关于x的分式方程
x-22-x
1有增根,则m的值为
(D)
B.1
D
x+1
16.当
2与
互为相
反数
标题截图放置居中位置
知识要点全练
夯奥基础
知识点1分式方程的概念
1.下列方程是分式方程的是
2x=5
1=0
x-2
4x=0
2.下列方程是关于x的分式方程的是(D
3+x
B
6
2 x
b
24x-5
3.下列关于x,y的方程:
4
其中是分
b
式方程的有
(B)
A.1个B.2个C.3个D.4个
知识点2解分式方程
4.(2020哈尔滨)方程
的解为(D
B. x
259
大,x-3
(2020成都)已知x=2是分式方程
1的解,那么实数k的值为
D.6
x-1
6.若关于x的分式方程=无解,则m
的值为
(B)
(2020黑龙江)已知关于x的分式方程
k
4
的解为非正数,则k的取值范围是
A)
A.k≤-12
b.k
12
c.k
12
D.k<-12
若分式
与一的值相等,则x
x+2
9.(2020南京)方程
C
的解是x
1x+2
4
10.若2x-1=3(x-1)1,则x的值是2
11.若关于x的分式方程
ca
1的解为正数,则
x-1
的取值范围是a>1且a≠2
12.解方程:
x+1
4
(1)
x-1x2-1
解:方程两边同乘(x-1)(x+1),得
(x+1)2+4=(x-1)(x+1),∴x
检验:当x=-3时,(x-1)(x+1)≠0,
原方程的解是x
(2)
x2+3x
解:原方程可化为
x(x+3)x(x-1)
方程两边同乘x(x+3)(x-1),得
5(x-1)-(x+3)=0,∴x=2
检验:当x=2时,x(x+3)(x-1)≠0,
∴原方程的解是x=2
2 x
(3)
2(x-2)(x-3)
解:方程两边同乘(x-3)(x-2),得
a(
)=2x(x-2)
3x-1
2x2-4x
检验:当x=1时,(x-3)(x-2)≠0,
原方程的解为x=1
规律方法全练
提升能力
13.(2020齐齐哈尔)若关于x的分式方程
3.3
2
5的解为正数,则m的取值范
22—x
为
A.m<—10
B.m≤-10
C.m≥-10且m≠-6
D.m>-10且m≠-6
14.(2020重庆)若关于x的一元一次不等式组
3x-1
的解集为x≤a,且关于y的
sa
4
分式方程
1有正整数解,则所
有满足条件的整数a的值之积是
a)
14C.2
56
15.(2020遂宁)关于x的分式方程
x-22-x
1有增根,则m的值为
(D)
B.1
D
x+1
16.当
2与
互为相
反数
