第11章 专题训练(一)与三角形的边和角有关的计算 习题课件
文档属性
| 名称 | 第11章 专题训练(一)与三角形的边和角有关的计算 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:16:16 | ||
图片预览



文档简介
(共12张PPT)
类型1与高相关的计算
1.(原创题如图,在钝角△ABC中(∠ACB>90
(1)作BC边和AB边的高AM,CN
(2)若CN=3,AB=8,BC=6,求AM的长
解:(1)如图,线段AM,CN
为所求
(2)∵CN⊥AB,AM⊥BC,
由三角形面积公式得
△ABC
BC·AM
AB·CN,
AM=AB·CN
BO
AB=8,BC=6,CN=3,
8×3=4.
即AM的长为4
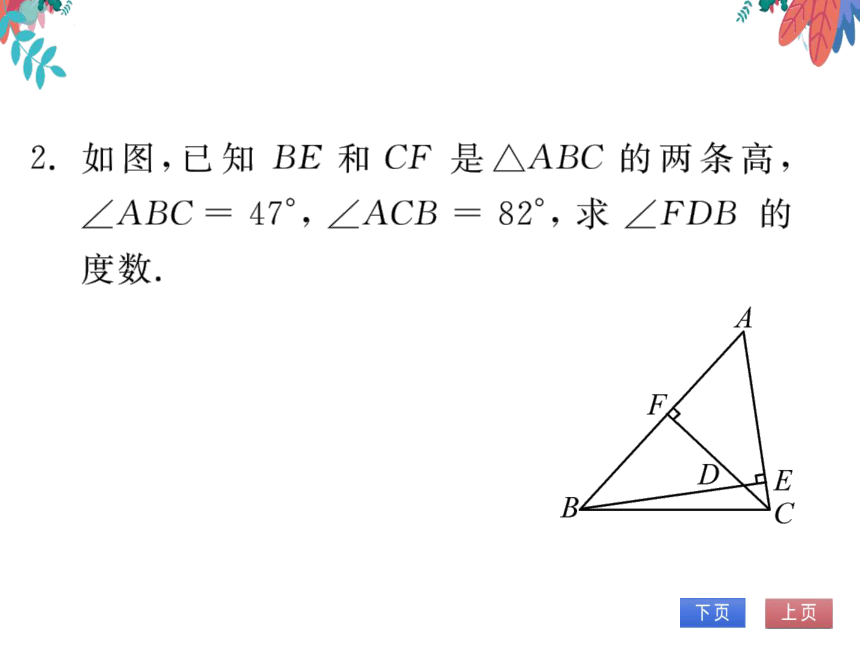
2.如图,已知BE和CF是△ABC的两条高,
∠ABC=47°,∠ACB=82,求∠FDB的
度数
解:∵BE和CF是△ABC的
两条高,
∠BFC=90°,∠BEC=90
在△BEC中,∠CBE=180°
∠BEC-∠ACB=8
在△BFC中,∠BCF=180°-∠BFC
∠ABC=43
∠FDB=∠CBE+∠BCF=51°
类型2与中线相关的计算
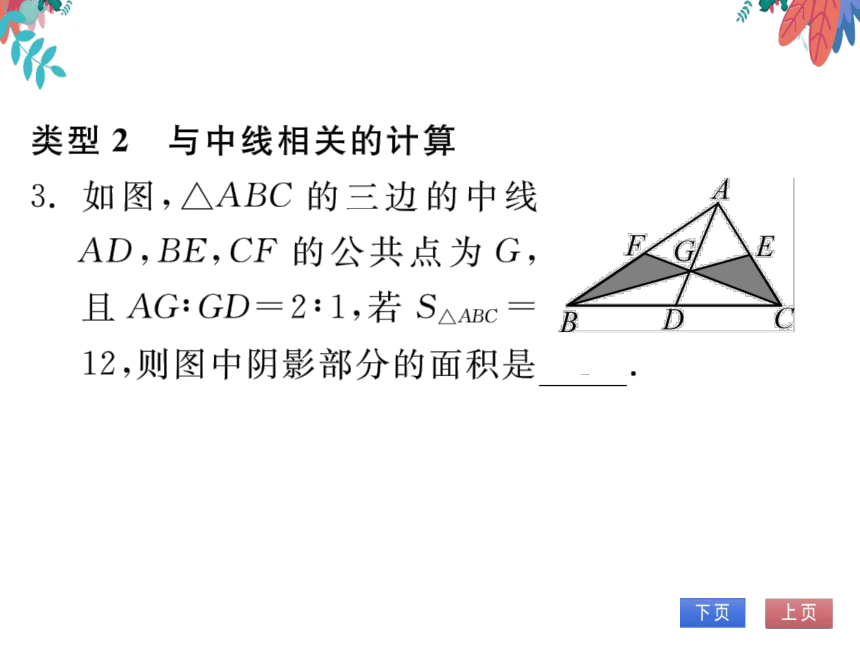
3.如图,△ABC的三边的中线
AD,BE,CF的公共点为G
且AG:GD=2:1,若S△ABC
12,则图中阴影部分的面积是4
解:设等腰三角形的腰长为x,底边长为y
2x+y=24,(2x+y=24,
根据题意,得
或
x=3
解得
或
6
y=10
等腰三角形各边的长分别为9cm,9cm,
6cm或7cm,7cm,10cm
类型3与角平分线相关的计算
5.(1)如图①,点P为△ABC的∠ABC和∠ACB
的平分线的交点,求证:∠P=90°+∠A
(2)如图②,点P为△ABC的∠ABC和外角
∠ACE的平分线的交点,求证:∠P
2∠A
(3)如图③,点P为△ABC的外角∠CBE和
∠BCF的平分线的交点,求证:∠P=90°
∠A.
证明:(1)∠P=180°—(∠PBC+∠PCB)
180
(∠ABC+∠ACB)=180°1
(180
A)=90°+∠A
(2)∠P=∠PCE-∠PBE=1
(∠ACE
ABC)
2<4
(3)∠P=180°-(∠PBC+∠PCB)=180
2(∠EBC+∠FCB)=180°1
∠A+
∠ACB+∠FCB)=180
(∠A+180°)
90
2∠A
类型1与高相关的计算
1.(原创题如图,在钝角△ABC中(∠ACB>90
(1)作BC边和AB边的高AM,CN
(2)若CN=3,AB=8,BC=6,求AM的长
解:(1)如图,线段AM,CN
为所求
(2)∵CN⊥AB,AM⊥BC,
由三角形面积公式得
△ABC
BC·AM
AB·CN,
AM=AB·CN
BO
AB=8,BC=6,CN=3,
8×3=4.
即AM的长为4
2.如图,已知BE和CF是△ABC的两条高,
∠ABC=47°,∠ACB=82,求∠FDB的
度数
解:∵BE和CF是△ABC的
两条高,
∠BFC=90°,∠BEC=90
在△BEC中,∠CBE=180°
∠BEC-∠ACB=8
在△BFC中,∠BCF=180°-∠BFC
∠ABC=43
∠FDB=∠CBE+∠BCF=51°
类型2与中线相关的计算
3.如图,△ABC的三边的中线
AD,BE,CF的公共点为G
且AG:GD=2:1,若S△ABC
12,则图中阴影部分的面积是4
解:设等腰三角形的腰长为x,底边长为y
2x+y=24,(2x+y=24,
根据题意,得
或
x=3
解得
或
6
y=10
等腰三角形各边的长分别为9cm,9cm,
6cm或7cm,7cm,10cm
类型3与角平分线相关的计算
5.(1)如图①,点P为△ABC的∠ABC和∠ACB
的平分线的交点,求证:∠P=90°+∠A
(2)如图②,点P为△ABC的∠ABC和外角
∠ACE的平分线的交点,求证:∠P
2∠A
(3)如图③,点P为△ABC的外角∠CBE和
∠BCF的平分线的交点,求证:∠P=90°
∠A.
证明:(1)∠P=180°—(∠PBC+∠PCB)
180
(∠ABC+∠ACB)=180°1
(180
A)=90°+∠A
(2)∠P=∠PCE-∠PBE=1
(∠ACE
ABC)
2<4
(3)∠P=180°-(∠PBC+∠PCB)=180
2(∠EBC+∠FCB)=180°1
∠A+
∠ACB+∠FCB)=180
(∠A+180°)
90
2∠A
