2021--2022学年人教版九年级数学上册22.3实际问题与二次函数-图形问题试卷(word版含答案)
文档属性
| 名称 | 2021--2022学年人教版九年级数学上册22.3实际问题与二次函数-图形问题试卷(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 615.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 06:28:44 | ||
图片预览


文档简介
人教版九年级上册数学22.3实际问题与二次函数-图形问题
一、单选题
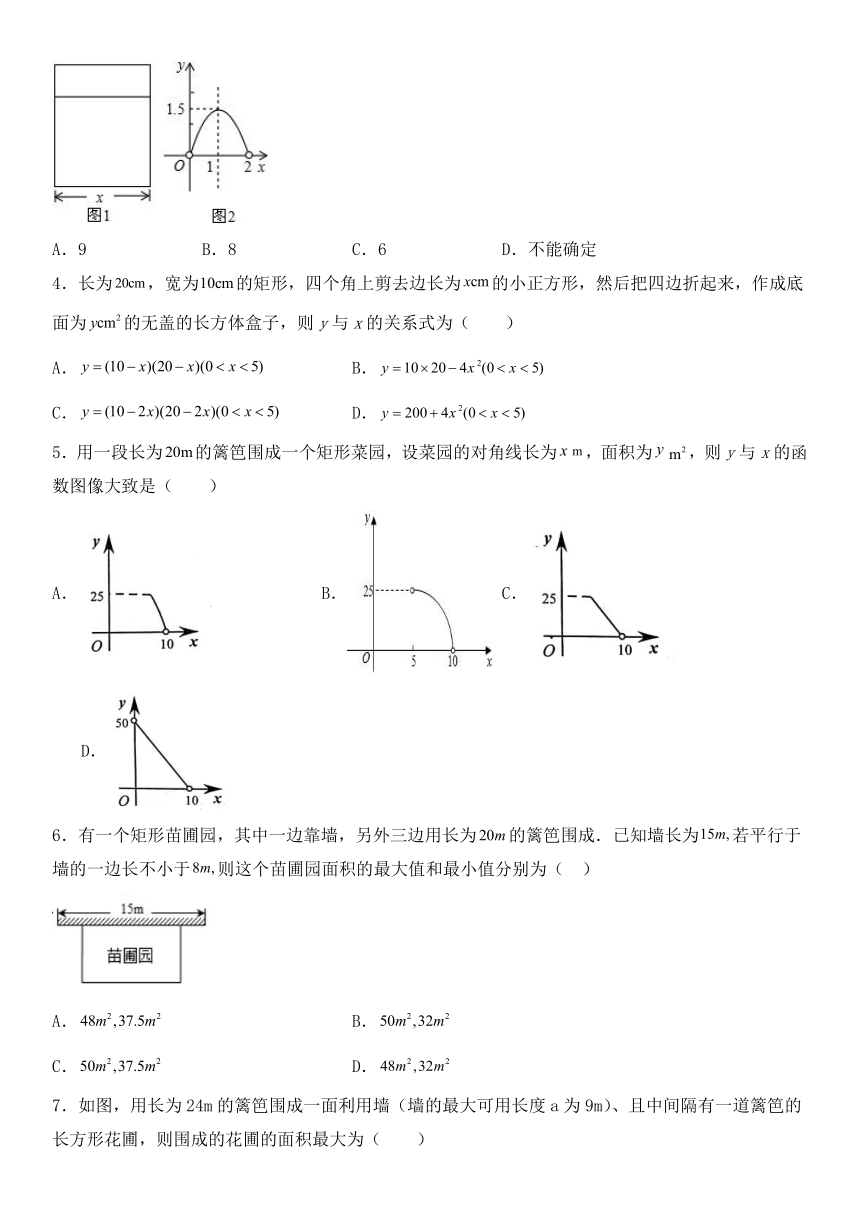
1.如图,中,,且,设直线 x=t截此三角形所得阴影部分的面积为S,则S与t之间的函数关系的图象为下列选项中的( )
A. B.
C. D.
2.如图,用一段长为30米的篱笆围成一个一边靠墙(墙的长度不限)的矩形菜园ABCD,设AB边长为x米,BC的长y米,菜园的面积为S(单位:平方米) .当x在一定范围内变化时,y和S都随x的变化而变化,则y与x,S与x满足的函数关系分别是( )
A.一次函数关系,二次函数关系 B.反比例函数关系,二次函数关系
C.一次函数关系,反比例函数关系 D.反比例函数关系,一次函数关系
3.用总长为a米的材料做成如图1的矩形窗框,设窗框的宽为x米,窗框的面积为y米2,y关于x的函数图象如图2,则a的值是( )
A.9 B.8 C.6 D.不能确定
4.长为,宽为的矩形,四个角上剪去边长为的小正方形,然后把四边折起来,作成底面为的无盖的长方体盒子,则y与x的关系式为( )
A. B.
C. D.
5.用一段长为的篱笆围成一个矩形菜园,设菜园的对角线长为,面积为,则y与x的函数图像大致是( )
A. B. C. D.
6.有一个矩形苗圃园,其中一边靠墙,另外三边用长为的篱笆围成.已知墙长为若平行于墙的一边长不小于则这个苗圃园面积的最大值和最小值分别为( )
A. B.
C. D.
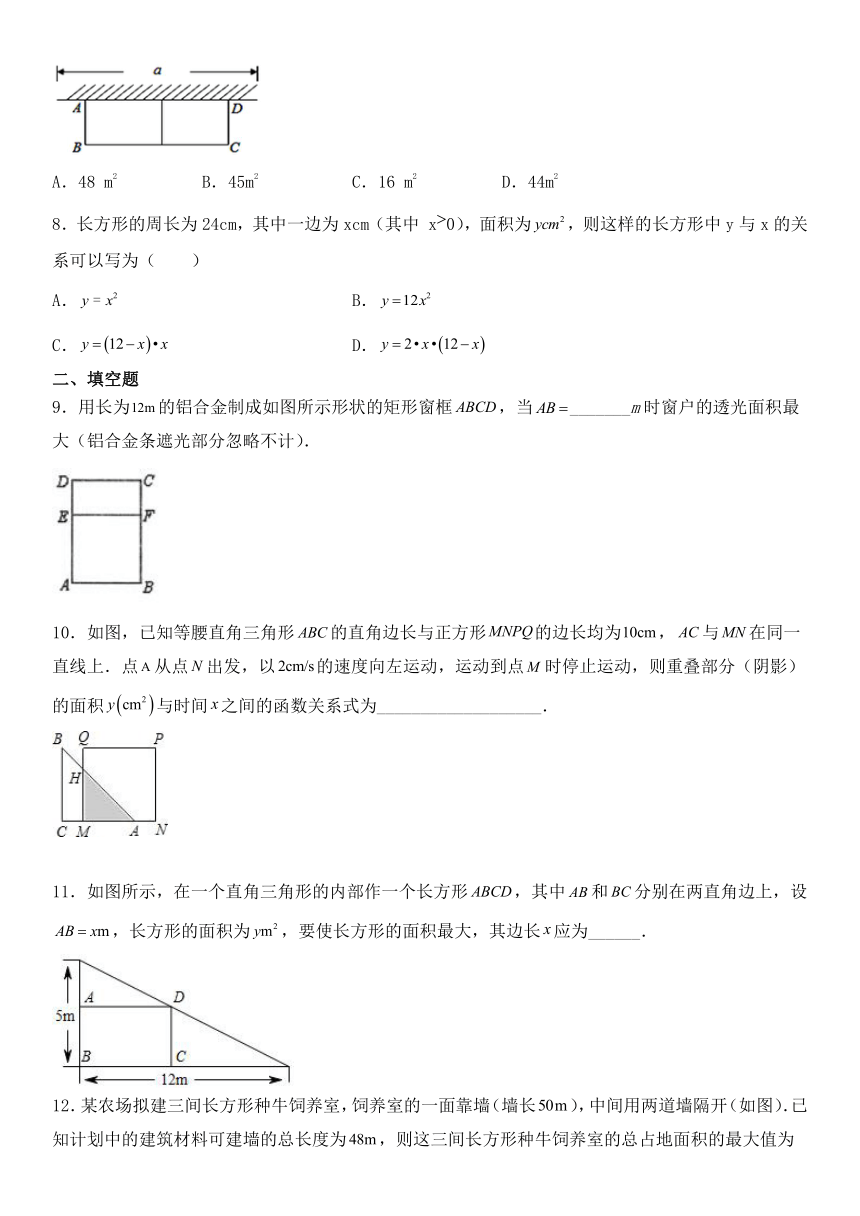
7.如图,用长为24m的篱笆围成一面利用墙(墙的最大可用长度a为9m)、且中间隔有一道篱笆的长方形花圃,则围成的花圃的面积最大为( )
A.48 m2 B.45m2 C.16 m2 D.44m2
8.长方形的周长为24cm,其中一边为xcm(其中 x0),面积为,则这样的长方形中y与x的关系可以写为( )
A. B.
C. D.
二、填空题
9.用长为的铝合金制成如图所示形状的矩形窗框,当_______m时窗户的透光面积最大(铝合金条遮光部分忽略不计).
10.如图,已知等腰直角三角形的直角边长与正方形的边长均为,与在同一直线上.点从点出发,以的速度向左运动,运动到点时停止运动,则重叠部分(阴影)的面积与时间之间的函数关系式为___________________.
11.如图所示,在一个直角三角形的内部作一个长方形,其中和分别在两直角边上,设,长方形的面积为,要使长方形的面积最大,其边长应为______.
12.某农场拟建三间长方形种牛饲养室,饲养室的一面靠墙(墙长),中间用两道墙隔开(如图).已知计划中的建筑材料可建墙的总长度为,则这三间长方形种牛饲养室的总占地面积的最大值为______.
13.如图,在平面直角坐标系中,正方形的顶点在轴正半轴上,顶点在轴正半轴上,若抛物线经过点,则的值为________.
14.已知抛物线与轴交于、两点,为抛物线上一点,且,则的坐标为_______.
15.如图,某水渠的横截面呈抛物线形,当水面宽8m时,水深4m,当水面下降1m时,水面宽为_____m.
16.如图,若被击打的小球飞行高度(单位:)与飞行时间(单位:)之间具有的关系为,则小球从飞出到落地所用的时间为_____.
三、解答题
17.现要用60米长的篱笆围成一个矩形场地(一边靠墙且墙长40米),应怎样围才能使矩形的面积S最大?最大是多少?
18.如图,有长为24m的篱笆,现一面利用墙(墙的最大可用长度a为10m),设花圃的宽AB为xm,面积为S.
(1)求S与x的函数关系式及x值的取值范围;
(2)要围成面积为45的花圃,AB的长是多少米?
(3)当AB的长是多少米时,围成的花圃的面积最大?(结果保留两位小数)
19.某社区决定把一块长为50m、宽30m的矩形空地建为居民健身广场,设计方案如图所示,阴影区域为绿化区(四块绿化区均为大小、形状都相同的矩形),空白区域为活动区,且四周的四个出口宽度相同,其宽度不小于14m,不大于26m,设绿化区较长边为xm,活动区的面积为ym2.
(1)求y与x的函数表达式并求出自变量x的取值范围,
(2)求活动区最大面积.
20.在矩形ABCD中,AB=5cm,BC=6cm,点P从点A开始沿边AB向终点B以1cm/s的速度移动,与此同时,点Q从点B开始沿边BC向终点C以2cm/s的速度移动.如果P、Q分别从A、B同时出发,当点Q运动到点C时,两点停止运动.设运动时间为t秒.
(1)填空:BQ= ,PB= (用含t的代数式表示);
(2)当t为何值时,PQ的长度等于5cm?
(3)是否存在t的值,使得五边形APQCD的面积等于26cm2?若存在,请求出此时t的值;若不存在,请说明理由.
(4)是否存在t的值,使△BPQ的面积最大,若存在,请直接写出此时t的值;若不存在,请说明理由.
参考答案
1.D
2.A
3.C
4.C
5.B
6.C
7.B
8.C
9.2
10.
11.
12.144
13.
14.(2,-1)或(2-,1),或(2+,1).
15.4
16.4.
解:依题意,令得:
∴
得:
解得:(舍去)或
∴即小球从飞出到落地所用的时间为
故答案为4.
17.
解:设垂直于墙的两边分别为x米,根据题意得:
,
∵,
∴当时,菜园面积最大,最大面积是450平方米,
此时矩形另一边为<40(符合题意).
答:当垂直于墙的两边分别为15米,矩形另一边为30米时,矩形的面积最大,最大面积为450平方米.
18.
(1)依题意,可知花圃宽为:m;长为:m;
花圃为长方形,
∴ ,
又宽为m;
∴ ,
可得:;
∴ ,;
(2)由(1)知,,;
∴ ,
又,当时,取得最大值为48;
∴ 花圃面积的最大值为48;
(3)由(2)可知,当时,取得最大值,即为
,故而不能围城面积为60的花圃;
19.
(1)四周的四个出口宽度相同,其宽度不小于14m,不大于26m,
设四个出口的宽度为,则,
,
则,
,
则绿化区较短边为,
设绿化区较长边为xm,活动区的面积为ym2,根据题意,
,
;
(2)由(1)可知
,
当时,随的增大而减小 ,
,
当时,取得最大值,最大值为,
活动区最大面积为.
20.
解:(1)由题意: ,,
故答案为,.
(2)由题意得:,
解得(不合题意,舍去),,
∴当t=2秒时,的长度等于.
(3)存在.理由如下:
长方形的面积是:,
使得五边形的面积等于26 ,
则的面积为,
即有:,
解得,.
当时,,不合题意,舍去,
即当时,使得五边形的面积等于26.
(4)存在,理由如下:
由(3)可知的面积为,
即当时,使得的面积最大,等于.
一、单选题
1.如图,中,,且,设直线 x=t截此三角形所得阴影部分的面积为S,则S与t之间的函数关系的图象为下列选项中的( )
A. B.
C. D.
2.如图,用一段长为30米的篱笆围成一个一边靠墙(墙的长度不限)的矩形菜园ABCD,设AB边长为x米,BC的长y米,菜园的面积为S(单位:平方米) .当x在一定范围内变化时,y和S都随x的变化而变化,则y与x,S与x满足的函数关系分别是( )
A.一次函数关系,二次函数关系 B.反比例函数关系,二次函数关系
C.一次函数关系,反比例函数关系 D.反比例函数关系,一次函数关系
3.用总长为a米的材料做成如图1的矩形窗框,设窗框的宽为x米,窗框的面积为y米2,y关于x的函数图象如图2,则a的值是( )
A.9 B.8 C.6 D.不能确定
4.长为,宽为的矩形,四个角上剪去边长为的小正方形,然后把四边折起来,作成底面为的无盖的长方体盒子,则y与x的关系式为( )
A. B.
C. D.
5.用一段长为的篱笆围成一个矩形菜园,设菜园的对角线长为,面积为,则y与x的函数图像大致是( )
A. B. C. D.
6.有一个矩形苗圃园,其中一边靠墙,另外三边用长为的篱笆围成.已知墙长为若平行于墙的一边长不小于则这个苗圃园面积的最大值和最小值分别为( )
A. B.
C. D.
7.如图,用长为24m的篱笆围成一面利用墙(墙的最大可用长度a为9m)、且中间隔有一道篱笆的长方形花圃,则围成的花圃的面积最大为( )
A.48 m2 B.45m2 C.16 m2 D.44m2
8.长方形的周长为24cm,其中一边为xcm(其中 x0),面积为,则这样的长方形中y与x的关系可以写为( )
A. B.
C. D.
二、填空题
9.用长为的铝合金制成如图所示形状的矩形窗框,当_______m时窗户的透光面积最大(铝合金条遮光部分忽略不计).
10.如图,已知等腰直角三角形的直角边长与正方形的边长均为,与在同一直线上.点从点出发,以的速度向左运动,运动到点时停止运动,则重叠部分(阴影)的面积与时间之间的函数关系式为___________________.
11.如图所示,在一个直角三角形的内部作一个长方形,其中和分别在两直角边上,设,长方形的面积为,要使长方形的面积最大,其边长应为______.
12.某农场拟建三间长方形种牛饲养室,饲养室的一面靠墙(墙长),中间用两道墙隔开(如图).已知计划中的建筑材料可建墙的总长度为,则这三间长方形种牛饲养室的总占地面积的最大值为______.
13.如图,在平面直角坐标系中,正方形的顶点在轴正半轴上,顶点在轴正半轴上,若抛物线经过点,则的值为________.
14.已知抛物线与轴交于、两点,为抛物线上一点,且,则的坐标为_______.
15.如图,某水渠的横截面呈抛物线形,当水面宽8m时,水深4m,当水面下降1m时,水面宽为_____m.
16.如图,若被击打的小球飞行高度(单位:)与飞行时间(单位:)之间具有的关系为,则小球从飞出到落地所用的时间为_____.
三、解答题
17.现要用60米长的篱笆围成一个矩形场地(一边靠墙且墙长40米),应怎样围才能使矩形的面积S最大?最大是多少?
18.如图,有长为24m的篱笆,现一面利用墙(墙的最大可用长度a为10m),设花圃的宽AB为xm,面积为S.
(1)求S与x的函数关系式及x值的取值范围;
(2)要围成面积为45的花圃,AB的长是多少米?
(3)当AB的长是多少米时,围成的花圃的面积最大?(结果保留两位小数)
19.某社区决定把一块长为50m、宽30m的矩形空地建为居民健身广场,设计方案如图所示,阴影区域为绿化区(四块绿化区均为大小、形状都相同的矩形),空白区域为活动区,且四周的四个出口宽度相同,其宽度不小于14m,不大于26m,设绿化区较长边为xm,活动区的面积为ym2.
(1)求y与x的函数表达式并求出自变量x的取值范围,
(2)求活动区最大面积.
20.在矩形ABCD中,AB=5cm,BC=6cm,点P从点A开始沿边AB向终点B以1cm/s的速度移动,与此同时,点Q从点B开始沿边BC向终点C以2cm/s的速度移动.如果P、Q分别从A、B同时出发,当点Q运动到点C时,两点停止运动.设运动时间为t秒.
(1)填空:BQ= ,PB= (用含t的代数式表示);
(2)当t为何值时,PQ的长度等于5cm?
(3)是否存在t的值,使得五边形APQCD的面积等于26cm2?若存在,请求出此时t的值;若不存在,请说明理由.
(4)是否存在t的值,使△BPQ的面积最大,若存在,请直接写出此时t的值;若不存在,请说明理由.
参考答案
1.D
2.A
3.C
4.C
5.B
6.C
7.B
8.C
9.2
10.
11.
12.144
13.
14.(2,-1)或(2-,1),或(2+,1).
15.4
16.4.
解:依题意,令得:
∴
得:
解得:(舍去)或
∴即小球从飞出到落地所用的时间为
故答案为4.
17.
解:设垂直于墙的两边分别为x米,根据题意得:
,
∵,
∴当时,菜园面积最大,最大面积是450平方米,
此时矩形另一边为<40(符合题意).
答:当垂直于墙的两边分别为15米,矩形另一边为30米时,矩形的面积最大,最大面积为450平方米.
18.
(1)依题意,可知花圃宽为:m;长为:m;
花圃为长方形,
∴ ,
又宽为m;
∴ ,
可得:;
∴ ,;
(2)由(1)知,,;
∴ ,
又,当时,取得最大值为48;
∴ 花圃面积的最大值为48;
(3)由(2)可知,当时,取得最大值,即为
,故而不能围城面积为60的花圃;
19.
(1)四周的四个出口宽度相同,其宽度不小于14m,不大于26m,
设四个出口的宽度为,则,
,
则,
,
则绿化区较短边为,
设绿化区较长边为xm,活动区的面积为ym2,根据题意,
,
;
(2)由(1)可知
,
当时,随的增大而减小 ,
,
当时,取得最大值,最大值为,
活动区最大面积为.
20.
解:(1)由题意: ,,
故答案为,.
(2)由题意得:,
解得(不合题意,舍去),,
∴当t=2秒时,的长度等于.
(3)存在.理由如下:
长方形的面积是:,
使得五边形的面积等于26 ,
则的面积为,
即有:,
解得,.
当时,,不合题意,舍去,
即当时,使得五边形的面积等于26.
(4)存在,理由如下:
由(3)可知的面积为,
即当时,使得的面积最大,等于.
同课章节目录
