等差数列及其通项公式
图片预览








文档简介
(共23张PPT)
等差数列及其通项公式
一、复习引入
1.什么是数列 什么是数列的项
按一定次序排成的一列数叫数列.数列中 的每一个数都叫做这个数列的项.
2.通项公式的概念
如果数列{an}的第n 项an与项数n之间的关系可以用一个公式来表示,这个公式就叫做这个数列的通项公式.
(1) 1 , 3 , 5 , 7 , 9 , 11 , 13 , 15
从第二项起每一项与它前一项的差都等于2
(2)-3 , 0 , 3 , 6 , 9 , 12 , 15 , 18
从第二项起每一项与它前一项的差都等于3
(3)70 , 60 , 50 , 40 , 30 , 20 , 10
从第二项起每一项与它前一项的差都等于-10
它们有什么共同的特点?
3.观察下列数列:
二、新课
1.等差数列的定义
一般地,如果一个数列从第二项起,每一项与它的前一项的差等于同一个常数d,那么这个数列就叫做等差数列。常数d叫做等差数列的公差。
即:an+1-an = d (n∈N﹡)
等差数列的定义如何用数学符号表示
它们都是等差数列 吗
(1)5,5,5,5,5,5,5,5,5
(2)0,2,4,6,8,10,12
(3)-1,1,-1,1,-1,1,-1,1
(4)1,2,3,5,7,9,11,13
是
是
不是
这些特别的数列有没有通项公式呢??
不是
2.等差数列的递推公式
an+1 = an + d (n∈N﹡)
3.等差数列的通项公式
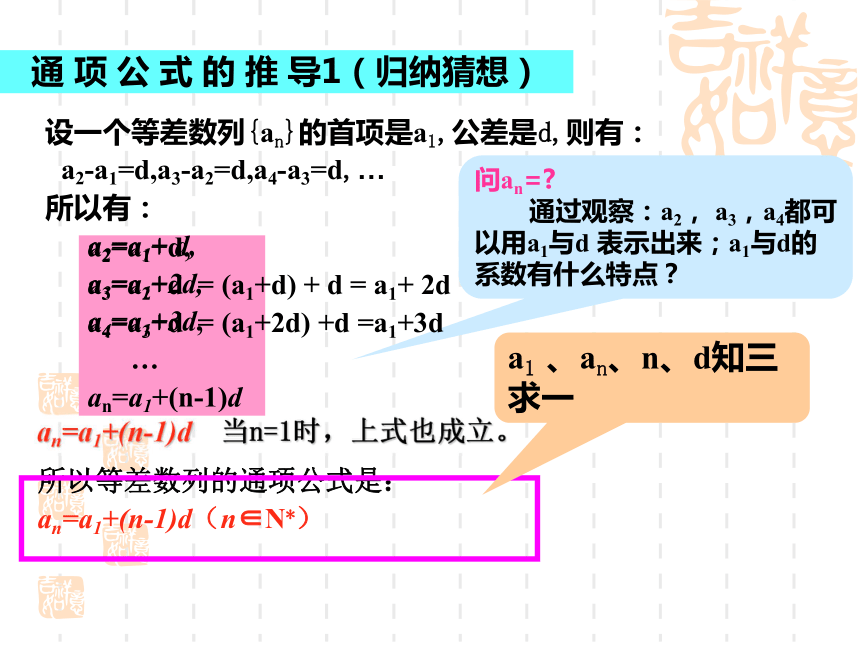
通 项 公 式 的 推 导1(归纳猜想)
设一个等差数列{an}的首项是a1,公差是d,则有:
a2-a1=d,a3-a2=d,a4-a3=d,…
所以有:
an=a1+(n-1)d 当n=1时,上式也成立。
所以等差数列的通项公式是:
an=a1+(n-1)d(n∈N*)
问an=
通过观察:a2, a3,a4都可以用a1与d 表示出来;a1与d的系数有什么特点?
a1 、an、n、d知三求一
…
a2=a1+ d,
a3=a1+2d,
a4=a1+3d,
…
an=a1+(n-1)d
a2=a1+d,
a3=a2+d = (a1+d) + d = a1+ 2d
a4=a3+d = (a1+2d) +d =a1+3d
叠加得
…
等差数列的通项公式推导2(叠加)
由an+1-an = d (n∈N﹡)得:
等差数列的通项公式:
①an=a1+(n-1)d(n∈N*)
②an=am+(n-m)d(n∈N*)
求公差的方法:
①d = an+1- an (n∈N﹡)
②d= (n∈N﹡)
③ d= (n、m∈N﹡)
a1 、an、n、d知三求一
③ -12,____, 0
在下列两数之间插入一个什么数,使三数成等差数列?它和前后两数之间有什么关系?
① 2,_____, 4
② -1,____, 5
3
-6
2
4.等差中项
定义:
如果a,A,b成等差数列,则A叫做a与b的等差中项。
定义:
如果a,A,b成等差数列,则A叫做a与b的等差中项。且
或 2A=a+b
注意: ①在一个等差数列中,从第2项起,每
一项(有穷数列的末项除外)都是它的前一项
与后一项的等差中项.
可见:如果三个数成等差数列,那么等差中
项等于另两项的算术平均数.
在等差数列:
a1,a2,a3,…an-1,an,an+1…中
如:在1,3,5,7,9,11,……中
2×5=3+7; 2×9=7+11 。。。。
即:在等差数列中{an}中,对任意连续的
三项, 都有
②三个数a,A,b成等差数列
A是a、b的等差中项。
例1:
指出下列数列中的等差数列,并求出公差和通项公式
(1)1,5,9,13,17,
(2)1,4,16,64,256,
(3)2,2,2,2,2,2,
例2.
(1)求等差数列8,5,2,…的第20项.
(2)-401是不是等差数列-5,-9,-13,…的项?如果是,是第几项?
例3.在等差数列{an}中,已知a3=10, a9=28,
求a12 。
解:由题意得
a1+2d=10
a1+8d=28
所以 a12=4+(12-1) ×3=37
解得: a1=4
d=3
变式:
已知a5=11, a8=5, 求等差数列{an}的通项公式.
例4. 课本P12.
例5.第一届现代奥运会于1896年在希腊雅典举行,此后每4年举行一次,奥运会如因故不能举行,届数照算。
(1)试写出由举行奥运会的年份构成的数列的通项公式
(2)2008年北京奥运会是第几届?2050年举行奥运会吗?
解:(1)由题意知,举行奥运会的年份构成的数列是一个以1896为首项,4为公差的等差数列。这个数列的通项公式为
an=1896+4(n-1)
=1892+4n(n∈N*)
(2) 假设an=2008, 由 2008=1892+4n, 得 n=29.
假设an=2050,2050=1892+4n 无正整数解.
答:所求通项公式为 an= 1892+4n(n∈N*) ,
2008年北京奥运会是第29届,2050年不举行奥运会
例6:某滑轮组由直径成等差数列的6个滑轮组成.已知最 小与最大的滑轮的直径分别为15和25cm,求中间四个滑轮的直径.
解:用{an}表示滑轮的直径所构成的等差数列,根据题意知
a1=15,a6=25
由等差数列的通项公式,得
a6=a1+(6-1)d,
即 25=15+5d,
d=2
由此得:a2=17,a3=19,a4=21,a5=23
答:中间的四个滑轮的直径顺次为17cm,19cm,21cm,23cm.
三、小结
1.等差数列的定义:
an+1-an = d (n∈N﹡)
2.等差数列的递推公式:
an+1 = an + d (n∈N﹡)
3.等差数列的通项公式:
①an=a1+(n-1)d(n∈N*)
②an=am+(n-m)d(n∈N*)
4.求公差的方法:
①d = an+1- an (n∈N﹡)
②d= (n∈N﹡)
③ d= (n、m∈N﹡)
5.等差中项:
①如果a,A,b成等差数列,则A叫做a与b的等差中项。且
②在等差数列:
a1,a2,a3,…an-1,an,an+1…中
②三个数a,A,b成等差数列
A是a、b的等差中项。
四、练习
课本:P13
五、作业
《练习册》P.3-A组-1~7,9,10,12
等差数列及其通项公式
一、复习引入
1.什么是数列 什么是数列的项
按一定次序排成的一列数叫数列.数列中 的每一个数都叫做这个数列的项.
2.通项公式的概念
如果数列{an}的第n 项an与项数n之间的关系可以用一个公式来表示,这个公式就叫做这个数列的通项公式.
(1) 1 , 3 , 5 , 7 , 9 , 11 , 13 , 15
从第二项起每一项与它前一项的差都等于2
(2)-3 , 0 , 3 , 6 , 9 , 12 , 15 , 18
从第二项起每一项与它前一项的差都等于3
(3)70 , 60 , 50 , 40 , 30 , 20 , 10
从第二项起每一项与它前一项的差都等于-10
它们有什么共同的特点?
3.观察下列数列:
二、新课
1.等差数列的定义
一般地,如果一个数列从第二项起,每一项与它的前一项的差等于同一个常数d,那么这个数列就叫做等差数列。常数d叫做等差数列的公差。
即:an+1-an = d (n∈N﹡)
等差数列的定义如何用数学符号表示
它们都是等差数列 吗
(1)5,5,5,5,5,5,5,5,5
(2)0,2,4,6,8,10,12
(3)-1,1,-1,1,-1,1,-1,1
(4)1,2,3,5,7,9,11,13
是
是
不是
这些特别的数列有没有通项公式呢??
不是
2.等差数列的递推公式
an+1 = an + d (n∈N﹡)
3.等差数列的通项公式
通 项 公 式 的 推 导1(归纳猜想)
设一个等差数列{an}的首项是a1,公差是d,则有:
a2-a1=d,a3-a2=d,a4-a3=d,…
所以有:
an=a1+(n-1)d 当n=1时,上式也成立。
所以等差数列的通项公式是:
an=a1+(n-1)d(n∈N*)
问an=
通过观察:a2, a3,a4都可以用a1与d 表示出来;a1与d的系数有什么特点?
a1 、an、n、d知三求一
…
a2=a1+ d,
a3=a1+2d,
a4=a1+3d,
…
an=a1+(n-1)d
a2=a1+d,
a3=a2+d = (a1+d) + d = a1+ 2d
a4=a3+d = (a1+2d) +d =a1+3d
叠加得
…
等差数列的通项公式推导2(叠加)
由an+1-an = d (n∈N﹡)得:
等差数列的通项公式:
①an=a1+(n-1)d(n∈N*)
②an=am+(n-m)d(n∈N*)
求公差的方法:
①d = an+1- an (n∈N﹡)
②d= (n∈N﹡)
③ d= (n、m∈N﹡)
a1 、an、n、d知三求一
③ -12,____, 0
在下列两数之间插入一个什么数,使三数成等差数列?它和前后两数之间有什么关系?
① 2,_____, 4
② -1,____, 5
3
-6
2
4.等差中项
定义:
如果a,A,b成等差数列,则A叫做a与b的等差中项。
定义:
如果a,A,b成等差数列,则A叫做a与b的等差中项。且
或 2A=a+b
注意: ①在一个等差数列中,从第2项起,每
一项(有穷数列的末项除外)都是它的前一项
与后一项的等差中项.
可见:如果三个数成等差数列,那么等差中
项等于另两项的算术平均数.
在等差数列:
a1,a2,a3,…an-1,an,an+1…中
如:在1,3,5,7,9,11,……中
2×5=3+7; 2×9=7+11 。。。。
即:在等差数列中{an}中,对任意连续的
三项, 都有
②三个数a,A,b成等差数列
A是a、b的等差中项。
例1:
指出下列数列中的等差数列,并求出公差和通项公式
(1)1,5,9,13,17,
(2)1,4,16,64,256,
(3)2,2,2,2,2,2,
例2.
(1)求等差数列8,5,2,…的第20项.
(2)-401是不是等差数列-5,-9,-13,…的项?如果是,是第几项?
例3.在等差数列{an}中,已知a3=10, a9=28,
求a12 。
解:由题意得
a1+2d=10
a1+8d=28
所以 a12=4+(12-1) ×3=37
解得: a1=4
d=3
变式:
已知a5=11, a8=5, 求等差数列{an}的通项公式.
例4. 课本P12.
例5.第一届现代奥运会于1896年在希腊雅典举行,此后每4年举行一次,奥运会如因故不能举行,届数照算。
(1)试写出由举行奥运会的年份构成的数列的通项公式
(2)2008年北京奥运会是第几届?2050年举行奥运会吗?
解:(1)由题意知,举行奥运会的年份构成的数列是一个以1896为首项,4为公差的等差数列。这个数列的通项公式为
an=1896+4(n-1)
=1892+4n(n∈N*)
(2) 假设an=2008, 由 2008=1892+4n, 得 n=29.
假设an=2050,2050=1892+4n 无正整数解.
答:所求通项公式为 an= 1892+4n(n∈N*) ,
2008年北京奥运会是第29届,2050年不举行奥运会
例6:某滑轮组由直径成等差数列的6个滑轮组成.已知最 小与最大的滑轮的直径分别为15和25cm,求中间四个滑轮的直径.
解:用{an}表示滑轮的直径所构成的等差数列,根据题意知
a1=15,a6=25
由等差数列的通项公式,得
a6=a1+(6-1)d,
即 25=15+5d,
d=2
由此得:a2=17,a3=19,a4=21,a5=23
答:中间的四个滑轮的直径顺次为17cm,19cm,21cm,23cm.
三、小结
1.等差数列的定义:
an+1-an = d (n∈N﹡)
2.等差数列的递推公式:
an+1 = an + d (n∈N﹡)
3.等差数列的通项公式:
①an=a1+(n-1)d(n∈N*)
②an=am+(n-m)d(n∈N*)
4.求公差的方法:
①d = an+1- an (n∈N﹡)
②d= (n∈N﹡)
③ d= (n、m∈N﹡)
5.等差中项:
①如果a,A,b成等差数列,则A叫做a与b的等差中项。且
②在等差数列:
a1,a2,a3,…an-1,an,an+1…中
②三个数a,A,b成等差数列
A是a、b的等差中项。
四、练习
课本:P13
五、作业
《练习册》P.3-A组-1~7,9,10,12
