3.1.2用二分法求方程的近试解
图片预览








文档简介
(共32张PPT)
用二分法求方程的近似解
【教学难点】恰当地使用信息技术工具,利用二分法求给定精确度的方程的近似解.
【教学重点】通过用二分法求方程的近似解,体会函数的零点与方程根之间的联系,初步形成用函数观点处理问题的意识.
【教学目标】
通过具体实例理解二分法的概念及其适用条件;
能借助计算器用二分法求方程的近似解,并了解这一数学思想,为学习算法做准备;体会数学逼近过程,感受精确与近似的相对统一.
创设情境
组织探究
探索发现
尝试练习
作业回馈
课外活动
由二分查找及高次多项式方程的求根问题引入
二分法的意义、算法思想及方法步骤
体会函数零点的意义,明确二分法的适用范围
二分法的算法思想及方法步骤,初步应用二分法解决简单问题
二分法应用于实际
二分法为什么可以逼近零点的再分析
追寻阿贝尔和伽罗瓦
创设情境-材料一:
1.(第六届全国青少年信息学(计算机)奥林匹克分区联赛提高组初赛试题第15题)某数列有1000个各不相同的单元,由低至高按序排列;现要对该数列进行二分法检索(binary-search),在最坏的情况下,需检索( )个单元.
A.1000 B.10 C.100 D.500
高次多项式方程公式解的探索史料
由于实际问题的需要,我们经常需要寻求函数的零点(即的根),对于为一次或二次函数,我们有熟知的公式解法(二次时,称为求根公式).在十六世纪,已找到了三次和四次函数的求根公式,但对于高于4次的函数,类似的努力却一直没有成功,到了十九世纪,根据阿贝尔(Abel)和伽罗瓦(Galois)的研究,人们认识到高于4次的代数方程不存在求根公式,亦即,不存在用四则运算及根号表示的一般的公式解.同时,即使对于3次和4次的代数方程,其公式解的表示也相当复杂,一般来讲并不适宜作具体计算.因此对于高次多项式函数及其它的一些函数,有必要寻求其零点的近似解的方法,这是一个在计算数学中十分重要的课题.
创设情境-材料二:
1.函数的零点
2.方程的根与函数零点的关系
对于函数y=f(x),我们把使f(x)=0的实数根叫做函数y=f(x)的零点. (zero point).
函数y=f(x)的零点就是方程f(x)=0的实数根,也就是函数y=f(x)的图象与x轴的交点的横坐标.
所以 方程f(x)=0有实数根
函数y=f(x)的图象与x轴有交点
函数y=f(x)有零点
复习回顾
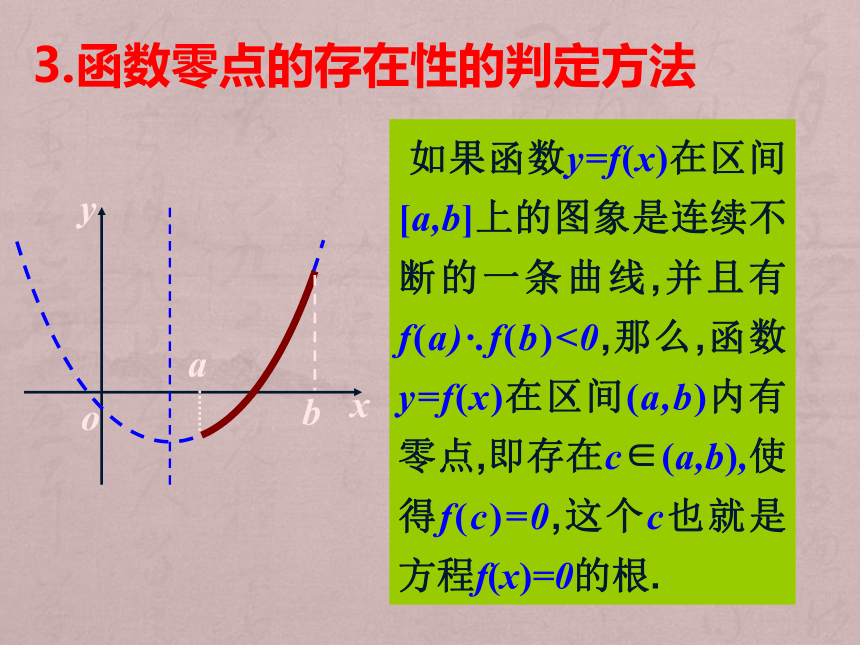
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·.f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
3.函数零点的存在性的判定方法
x
y
o
a
b
例1.求函数f(x)=x3-3x2+2x-6 在区间[0,4]内的变号零点.
解: f(0)=-6<0 , f(4)=18>0.
端点(中点)坐标
中点的函数值
取区间
[0,4]
[2,4]
X1=(0+4)/2=2
X2=(2+4)/2=3
f(x1)=f(2)=-6<0
f(x2)=f(3)=0
由上式计算可知,x2=3就是所求函数的一个零点.
组织探究(1)
x
y
o
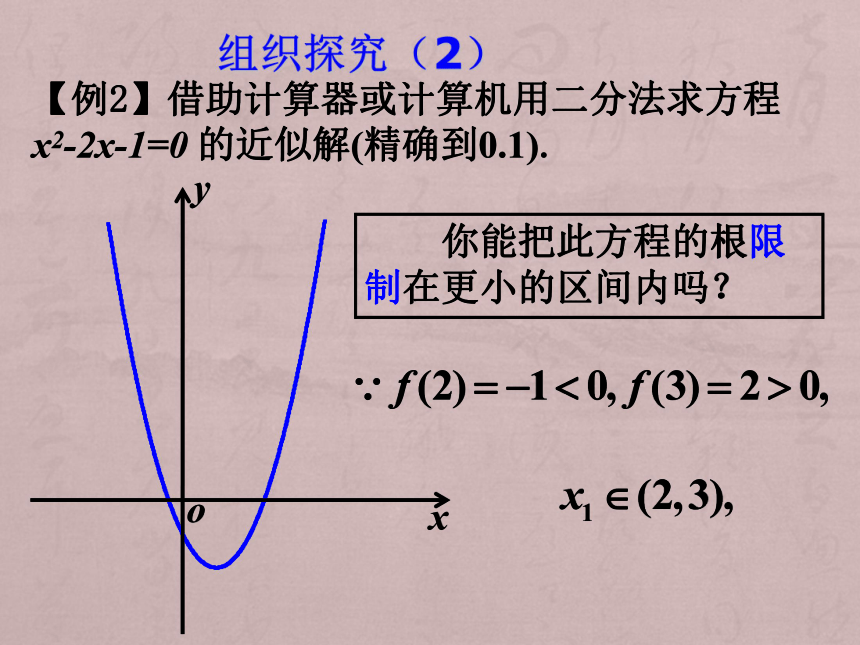
【例2】借助计算器或计算机用二分法求方程 x2-2x-1=0 的近似解(精确到0.1).
你能把此方程的根限制在更小的区间内吗?
组织探究(2)
x
y
o
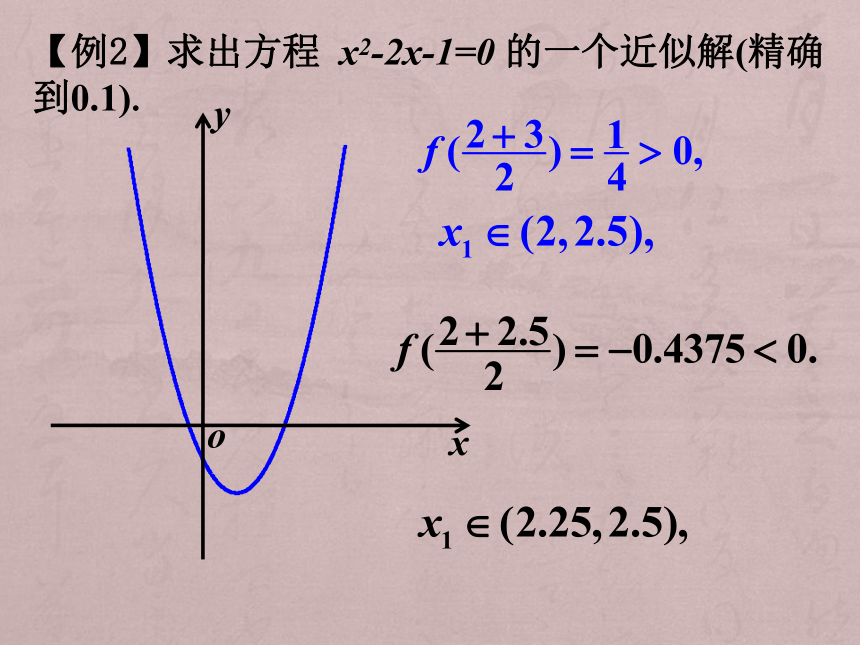
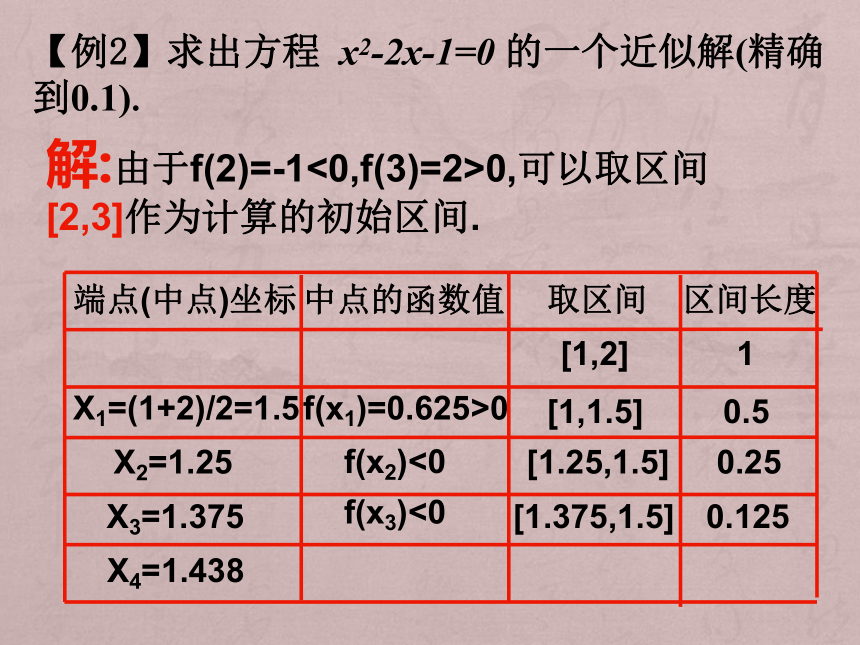
【例2】求出方程 x2-2x-1=0 的一个近似解(精确到0.1).
解:由于f(2)=-1<0,f(3)=2>0,可以取区间[2,3]作为计算的初始区间.
端点(中点)坐标
中点的函数值
取区间
区间长度
[1,2]
[1,1.5]
[1.25,1.5]
[1.375,1.5]
1
0.5
0.25
0.125
X1=(1+2)/2=1.5
X2=1.25
X3=1.375
X4=1.438
f(x1)=0.625>0
f(x2)<0
f(x3)<0
【例2】求出方程 x2-2x-1=0 的一个近似解(精确到0.1).
由上表的计算可知,区间[2.375,2.4375]的长度小于0.1,所以这个区间的中点x3=2.4063可作为所求函数误差不超过0.1的一个正实数零点的近似值.
用二分法求函数变号零点的一般步骤:
1.勘根定理,求出初始区间
2.进行计算,确定下一区间
3.循环进行,达到精确要求
2.二分法:对于在区间[a,b]上连续不断,且f(a) ·f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法(bisection).
3.给定精确度ε,用二分法求函数f(x)零点近似值的步骤如下:
1.确定区间[a,b],验证f(a)f(b)<0,给定精确度ε;
2.求区间(a,b)的中点x1;
3.计算f(x1);
(1)若f(x1)=0,则x1就是函数的零点;
(2)若f(a)f(x1)<0,则令b=x1(此时零x0 (a,x1));
(3)若f(x1)f(b)<0,则令a=x1(此时零点x0 (x1,b));
(4)判断是否达到精确度ε,即若|a-b|<ε,则得到零点近似值a(或b);否则重复2~4.
思考:一元二次方程可以用公式求根,但是可以用公式来求出方程lnx+2x-6=0的根吗?
求方程f(x)=0的实数根,就是要确定函数y=f(x)的零点.
区间 中点的值 中点函数近似值
(2,3) 2.5 -0.084
(2.5,3) 2.75 0.512
(2.5,2.75) 2.625 0.215
(2.5,2.625) 2.5625 0.066
(2.5,2.5625) 2.53125 -0.009
(2.53125,2.5625) 2.546875 0.029
(2.53125,2.546875) 2.5390625 0.010
(2.53125,2.5390625) 2.53515625 0.001
二分法及步骤:
对于在区间[a,b]上连续不断,且满足f(a)·f(b)<0的函数,通过不断地把函数y=f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.
给定精度 ,用二分法求函数的零点近似值的步骤如下:
1.确定区间 [a,b] ,验证 f(a)·f(b)<0 ,给定精度 ;
2.求区间 [a,b] 的中点x1;
3.计算:
(1) 若 f(x1)=0,则就是函数的零点;
(2) 若 f(a)·f(x1)<0,则令 b=x1(此时零点x0 (a,x1) );
(3) 若 f(x1) ·f(b)<0,则令 a= x1 (此时零点 x0 (x1,b) );
4.判断是否达到精度 ;
即若|a-b|< ,则得到零点近似值a(或b);否则重复步骤2~4.
二分法定义:
对于区间[a,b]上连续不断、且f(a) f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法(bisection)
end
二分法的解题步骤
给定精确度
,用二分法求函数f(x)零点近似解的步骤如下:
,给定精确度 ;
⑴确定区间[a,b],验证
⑵求区间(a,b)的中点 ;
⑶计算f( );
若f(
)=0,则
就是函数的零点;
②若
,则令b=
(
);
此时零点
③若
,则令a=
(此时零点
);
⑷判断是否达到精确度
:即若|a-b|<
,则得到零点近似值
为a(或b);否则重复⑵~⑷
end
例2.借助计算器或计算机用二分法求方程
的近似解(精确到0.1).
x 0 1 2 3 4 5 6 7 8
f(x)=2x+3x-7 -6 -2 3 10 21 40 75 142 237
例2 借助计算器或计算机用二分法求方程2x+3x=7的近似解(精确度0.1).
计算[a, b]中点c
计算并判定f(c)的符号,确定新的区间,
(判定知步长>ε)
确定零点近似解所在区间
[a, b],
迭代直至步长<ε
得到近似解
解:
原方程即
观察图像,
所以,原方程的近似解可取1.4375。
函数零点的性质
从“数”的角度看:即是使 f(x)=0 的实数;
从“形”的角度看:即是函数 f(x) 的图象与 x 轴交点的横坐标;
若函数 f(x) 的图象在 x=x0 处与 x 轴相切,则零点 x0 通常称为不变号零点;
若函数 f(x) 的图象在 x=x0 处与 x 轴相交,则零点 x0 通常称为变号零点.
二分法的条件 f(a)·f(b)<0 表明用二分法求函数的近似零点都是指变号零点.
教材P106练习1、2题;
教材P108习题3.1(A组)第1、2题;
求方程 log3x+x=3的解的个数及其大致所在区间;
求方程 0.9x-2x/21=0 的实数解的个数;
探究函数 y=0.3x与函数 y=log0.3x的图象有无交点,如有交点,求出交点,或给出一个与交点距离不超过 0.1 的点.
1、用二分法求函数
在区间(0,1)内的零点(精确到0.1)
解:
由题设可知:
所以,函数
区间(0,1)内有一个零点.
下面用二分法求函数在区间(0,1)内的零点
取区间(0,1)的中点
再取区间(0.5,1)的中点
所以……
教材P108习题3.1(A组)第3~6题、(B组)第4题;
提高作业:
1. 已知函数 f(x)=2(m+2)x2+4mx+2m-1
m为何值时,函数的图象与x轴有两个交点?
如果函数的一个零点在原点,求m的值.
2.借助于计算机或计算器,用二分法求函数 f(x)=x3-2 的零点(精确到 0.01);
3.用二分法求的 3 的立方根近似值(精确到0.01).
课堂小结
1.本节学习的主要数学知识
二分法的定义
二分法求函数零点的近似值的步骤.
2.本节应用的数学思想方法
体会信息技术的应用
二分法渗透了极限和算法的思想
说说方程的根与函数的零点的关系,并给出判定方程在某个区间存在根的基本步骤,及方程根的个数的判定方法;
谈谈通过学习求函数的零点和求方程的近似解,对数学有了哪些新的认识?
收获与体会
查找有关系资料或利用internet查找有关高次代数方程的解的研究史料,追寻阿贝尔(Abel)和伽罗瓦(Galois),增强探索精神,培养创新意识.
课后思考
第二教材:P129 页底的步骤
P130 例2 2
P132 1—9 11、14
P108 第3题
1.确定区间[a,b],验证f(a)·f(b)<0,给定精确度ε;
2.求区间(a,b)的中点x1;
3.计算f(x1);
⑴若f(x1)=0,则x1就是函数的零点;
⑵若f(a)·f(x1)<0,
则令b=x1(此时零点x0∈(a,x1));
⑶若f(x1)·f(b)<0,
则令a=x1(此时零点x0∈(x1,b))
4.判断是否达到精确度ε:即若|a-b|<ε,则得到零点近似值b(或a);否则重复2~4.
用二分法求方程的近似解
【教学难点】恰当地使用信息技术工具,利用二分法求给定精确度的方程的近似解.
【教学重点】通过用二分法求方程的近似解,体会函数的零点与方程根之间的联系,初步形成用函数观点处理问题的意识.
【教学目标】
通过具体实例理解二分法的概念及其适用条件;
能借助计算器用二分法求方程的近似解,并了解这一数学思想,为学习算法做准备;体会数学逼近过程,感受精确与近似的相对统一.
创设情境
组织探究
探索发现
尝试练习
作业回馈
课外活动
由二分查找及高次多项式方程的求根问题引入
二分法的意义、算法思想及方法步骤
体会函数零点的意义,明确二分法的适用范围
二分法的算法思想及方法步骤,初步应用二分法解决简单问题
二分法应用于实际
二分法为什么可以逼近零点的再分析
追寻阿贝尔和伽罗瓦
创设情境-材料一:
1.(第六届全国青少年信息学(计算机)奥林匹克分区联赛提高组初赛试题第15题)某数列有1000个各不相同的单元,由低至高按序排列;现要对该数列进行二分法检索(binary-search),在最坏的情况下,需检索( )个单元.
A.1000 B.10 C.100 D.500
高次多项式方程公式解的探索史料
由于实际问题的需要,我们经常需要寻求函数的零点(即的根),对于为一次或二次函数,我们有熟知的公式解法(二次时,称为求根公式).在十六世纪,已找到了三次和四次函数的求根公式,但对于高于4次的函数,类似的努力却一直没有成功,到了十九世纪,根据阿贝尔(Abel)和伽罗瓦(Galois)的研究,人们认识到高于4次的代数方程不存在求根公式,亦即,不存在用四则运算及根号表示的一般的公式解.同时,即使对于3次和4次的代数方程,其公式解的表示也相当复杂,一般来讲并不适宜作具体计算.因此对于高次多项式函数及其它的一些函数,有必要寻求其零点的近似解的方法,这是一个在计算数学中十分重要的课题.
创设情境-材料二:
1.函数的零点
2.方程的根与函数零点的关系
对于函数y=f(x),我们把使f(x)=0的实数根叫做函数y=f(x)的零点. (zero point).
函数y=f(x)的零点就是方程f(x)=0的实数根,也就是函数y=f(x)的图象与x轴的交点的横坐标.
所以 方程f(x)=0有实数根
函数y=f(x)的图象与x轴有交点
函数y=f(x)有零点
复习回顾
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·.f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
3.函数零点的存在性的判定方法
x
y
o
a
b
例1.求函数f(x)=x3-3x2+2x-6 在区间[0,4]内的变号零点.
解: f(0)=-6<0 , f(4)=18>0.
端点(中点)坐标
中点的函数值
取区间
[0,4]
[2,4]
X1=(0+4)/2=2
X2=(2+4)/2=3
f(x1)=f(2)=-6<0
f(x2)=f(3)=0
由上式计算可知,x2=3就是所求函数的一个零点.
组织探究(1)
x
y
o
【例2】借助计算器或计算机用二分法求方程 x2-2x-1=0 的近似解(精确到0.1).
你能把此方程的根限制在更小的区间内吗?
组织探究(2)
x
y
o
【例2】求出方程 x2-2x-1=0 的一个近似解(精确到0.1).
解:由于f(2)=-1<0,f(3)=2>0,可以取区间[2,3]作为计算的初始区间.
端点(中点)坐标
中点的函数值
取区间
区间长度
[1,2]
[1,1.5]
[1.25,1.5]
[1.375,1.5]
1
0.5
0.25
0.125
X1=(1+2)/2=1.5
X2=1.25
X3=1.375
X4=1.438
f(x1)=0.625>0
f(x2)<0
f(x3)<0
【例2】求出方程 x2-2x-1=0 的一个近似解(精确到0.1).
由上表的计算可知,区间[2.375,2.4375]的长度小于0.1,所以这个区间的中点x3=2.4063可作为所求函数误差不超过0.1的一个正实数零点的近似值.
用二分法求函数变号零点的一般步骤:
1.勘根定理,求出初始区间
2.进行计算,确定下一区间
3.循环进行,达到精确要求
2.二分法:对于在区间[a,b]上连续不断,且f(a) ·f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法(bisection).
3.给定精确度ε,用二分法求函数f(x)零点近似值的步骤如下:
1.确定区间[a,b],验证f(a)f(b)<0,给定精确度ε;
2.求区间(a,b)的中点x1;
3.计算f(x1);
(1)若f(x1)=0,则x1就是函数的零点;
(2)若f(a)f(x1)<0,则令b=x1(此时零x0 (a,x1));
(3)若f(x1)f(b)<0,则令a=x1(此时零点x0 (x1,b));
(4)判断是否达到精确度ε,即若|a-b|<ε,则得到零点近似值a(或b);否则重复2~4.
思考:一元二次方程可以用公式求根,但是可以用公式来求出方程lnx+2x-6=0的根吗?
求方程f(x)=0的实数根,就是要确定函数y=f(x)的零点.
区间 中点的值 中点函数近似值
(2,3) 2.5 -0.084
(2.5,3) 2.75 0.512
(2.5,2.75) 2.625 0.215
(2.5,2.625) 2.5625 0.066
(2.5,2.5625) 2.53125 -0.009
(2.53125,2.5625) 2.546875 0.029
(2.53125,2.546875) 2.5390625 0.010
(2.53125,2.5390625) 2.53515625 0.001
二分法及步骤:
对于在区间[a,b]上连续不断,且满足f(a)·f(b)<0的函数,通过不断地把函数y=f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.
给定精度 ,用二分法求函数的零点近似值的步骤如下:
1.确定区间 [a,b] ,验证 f(a)·f(b)<0 ,给定精度 ;
2.求区间 [a,b] 的中点x1;
3.计算:
(1) 若 f(x1)=0,则就是函数的零点;
(2) 若 f(a)·f(x1)<0,则令 b=x1(此时零点x0 (a,x1) );
(3) 若 f(x1) ·f(b)<0,则令 a= x1 (此时零点 x0 (x1,b) );
4.判断是否达到精度 ;
即若|a-b|< ,则得到零点近似值a(或b);否则重复步骤2~4.
二分法定义:
对于区间[a,b]上连续不断、且f(a) f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法(bisection)
end
二分法的解题步骤
给定精确度
,用二分法求函数f(x)零点近似解的步骤如下:
,给定精确度 ;
⑴确定区间[a,b],验证
⑵求区间(a,b)的中点 ;
⑶计算f( );
若f(
)=0,则
就是函数的零点;
②若
,则令b=
(
);
此时零点
③若
,则令a=
(此时零点
);
⑷判断是否达到精确度
:即若|a-b|<
,则得到零点近似值
为a(或b);否则重复⑵~⑷
end
例2.借助计算器或计算机用二分法求方程
的近似解(精确到0.1).
x 0 1 2 3 4 5 6 7 8
f(x)=2x+3x-7 -6 -2 3 10 21 40 75 142 237
例2 借助计算器或计算机用二分法求方程2x+3x=7的近似解(精确度0.1).
计算[a, b]中点c
计算并判定f(c)的符号,确定新的区间,
(判定知步长>ε)
确定零点近似解所在区间
[a, b],
迭代直至步长<ε
得到近似解
解:
原方程即
观察图像,
所以,原方程的近似解可取1.4375。
函数零点的性质
从“数”的角度看:即是使 f(x)=0 的实数;
从“形”的角度看:即是函数 f(x) 的图象与 x 轴交点的横坐标;
若函数 f(x) 的图象在 x=x0 处与 x 轴相切,则零点 x0 通常称为不变号零点;
若函数 f(x) 的图象在 x=x0 处与 x 轴相交,则零点 x0 通常称为变号零点.
二分法的条件 f(a)·f(b)<0 表明用二分法求函数的近似零点都是指变号零点.
教材P106练习1、2题;
教材P108习题3.1(A组)第1、2题;
求方程 log3x+x=3的解的个数及其大致所在区间;
求方程 0.9x-2x/21=0 的实数解的个数;
探究函数 y=0.3x与函数 y=log0.3x的图象有无交点,如有交点,求出交点,或给出一个与交点距离不超过 0.1 的点.
1、用二分法求函数
在区间(0,1)内的零点(精确到0.1)
解:
由题设可知:
所以,函数
区间(0,1)内有一个零点.
下面用二分法求函数在区间(0,1)内的零点
取区间(0,1)的中点
再取区间(0.5,1)的中点
所以……
教材P108习题3.1(A组)第3~6题、(B组)第4题;
提高作业:
1. 已知函数 f(x)=2(m+2)x2+4mx+2m-1
m为何值时,函数的图象与x轴有两个交点?
如果函数的一个零点在原点,求m的值.
2.借助于计算机或计算器,用二分法求函数 f(x)=x3-2 的零点(精确到 0.01);
3.用二分法求的 3 的立方根近似值(精确到0.01).
课堂小结
1.本节学习的主要数学知识
二分法的定义
二分法求函数零点的近似值的步骤.
2.本节应用的数学思想方法
体会信息技术的应用
二分法渗透了极限和算法的思想
说说方程的根与函数的零点的关系,并给出判定方程在某个区间存在根的基本步骤,及方程根的个数的判定方法;
谈谈通过学习求函数的零点和求方程的近似解,对数学有了哪些新的认识?
收获与体会
查找有关系资料或利用internet查找有关高次代数方程的解的研究史料,追寻阿贝尔(Abel)和伽罗瓦(Galois),增强探索精神,培养创新意识.
课后思考
第二教材:P129 页底的步骤
P130 例2 2
P132 1—9 11、14
P108 第3题
1.确定区间[a,b],验证f(a)·f(b)<0,给定精确度ε;
2.求区间(a,b)的中点x1;
3.计算f(x1);
⑴若f(x1)=0,则x1就是函数的零点;
⑵若f(a)·f(x1)<0,
则令b=x1(此时零点x0∈(a,x1));
⑶若f(x1)·f(b)<0,
则令a=x1(此时零点x0∈(x1,b))
4.判断是否达到精确度ε:即若|a-b|<ε,则得到零点近似值b(或a);否则重复2~4.
