第23章 高频考点集训　习题课件

(共20张PPT)
木章重难点突破
、本章高频考点集训
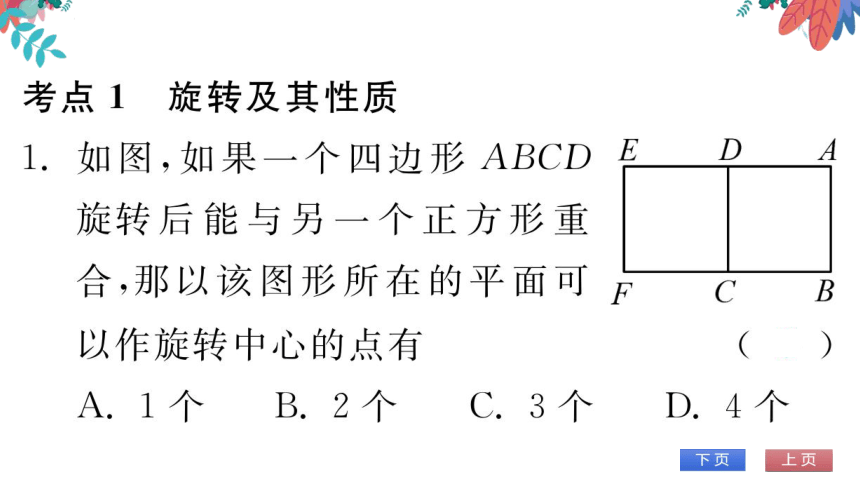
考点1旋转及其性质
如图,如果一个四边形 ABCD E
旋转后能与另一个正方形重
那以该图形所在的平面可
B
以作旋转中心的点有
A.1个B.2个C.3个D.4个
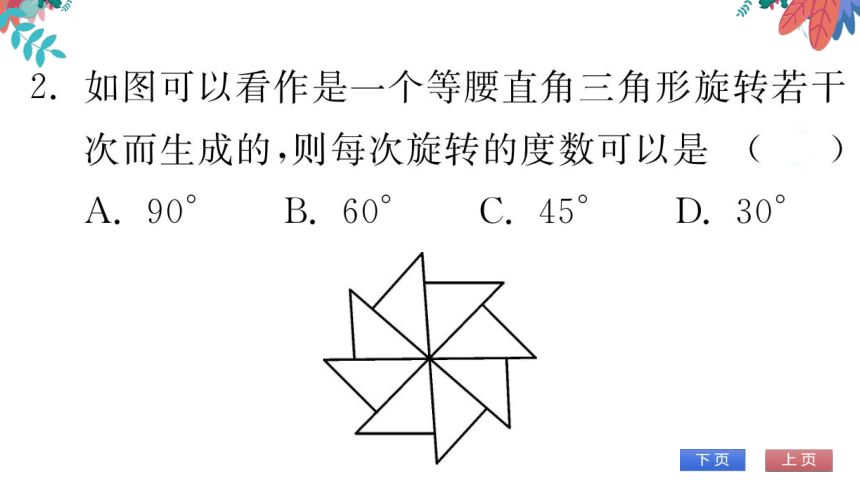
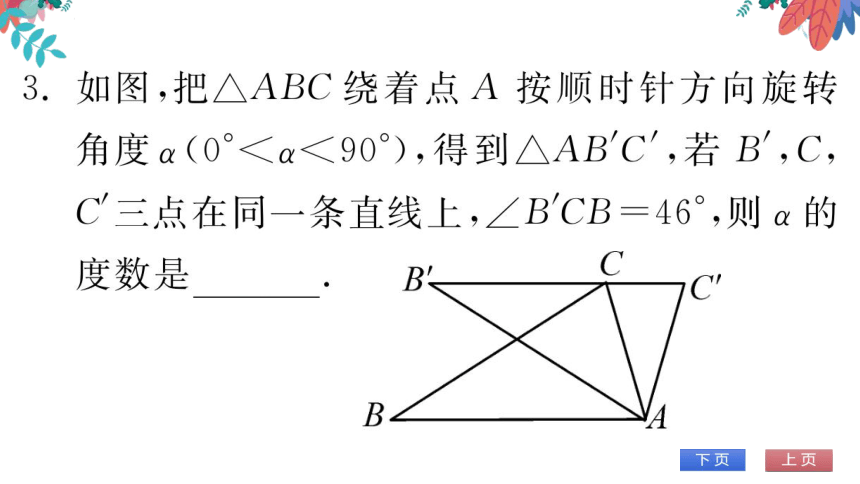
如图,把亼ABC绕着点A按顺时针方向旋转
角度a(0°<α<90°),得到△ABC,若B′,C
C三点在同一条直线上,∠BCB=46°,则α的
度数是46
B
C
B
(第3题图
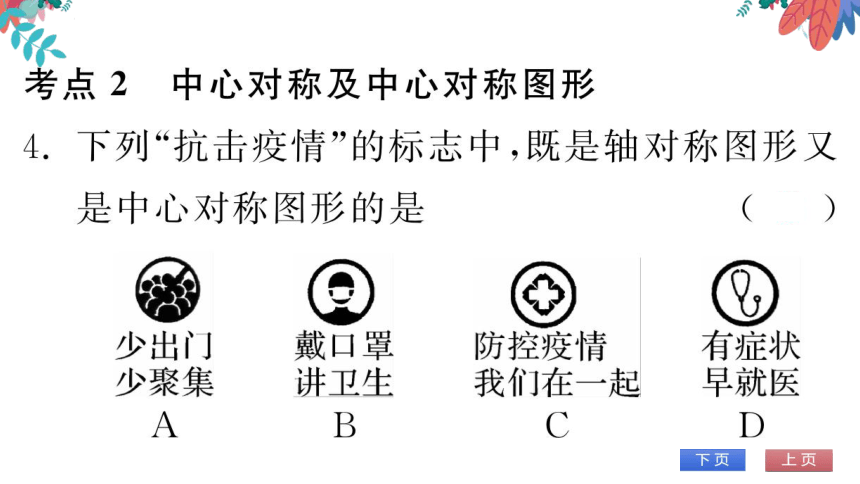
考点2中心对称及中心对称图形
4.下列“抗击疫情”的标志中,既是轴对称图形又
是中心对称图形的是
少出门戴口罩防控疫情
有症状
少聚集讲卫生我们在一起早就医
(2020绍兴)如图,点O为矩形ABCD的对称
中心,点E从点A出发沿AB向点B运动,移
动到点B停止,延长EO交CD于点F,则四
边形AECF形状的变化依次为
B
A.平行四边形→正方形→平行四边形→矩形
B.平行四边形→菱形→平行四边形→矩形
C.平行四边形→正方形→菱形→矩形
D.平行四边形→-菱形→正方形→矩形
C
B
E
(第5题图
考点3坐标系中的旋转
(孝感)在平面直角坐标系中,把点P(-5,3)向右
平移8个单位长度得到点P1,再将点P1绕原点
旋转90·得到点P2,则点P2的坐标是(D)
A.(3,-3)
B.(-3,3)
C.(3,3)或(-3,-3)D.(3,-3)或(-3,3)
(2020宁夏)如图,直线
x+4与x轴
轴分别交于A,B两点,把△AOB绕点B逆时
针旋转90°后得到△A1OB,则点A1的坐标是
12
4
O
A
AO
(第8题图)
考点4旋转中的计算
9.如图,边长为1的正方形ABCD绕点A逆时
针旋转30°得到正方形ABCD′,则图中阴影
部分的面积为
D.1
C
B
B
C
D
D
(第9题图)
0.如图,在△ABC中,∠BAC=30°,AB=√6,
AC=3,将△ABC绕点A逆时针旋转60°得
到△AB1C1,连接BC1,则BC1的长为(A
B.2√3
C.2√2
D.4
C
B
B
(第10题图)
B
第11题图)
2.如图,正方形ABCD中,将线段AD绕点A
页时针旋转30°得到线段AE,CE的延长线
交正方形ABCD的对角线BD于点F,
DFC的度数为120°
D
C
B
(第12题图)
3.如图,直角梯形ABCD中,AD∥BC,AB
BC,AD=2,将腰CD以D为中心逆时针旋
转90°至ED,连接AE,CE,△ADE的面积为
3,则BC的长为5