第23章 专题训练(五)利用旋转进行计算或证明 习题课件
文档属性
| 名称 | 第23章 专题训练(五)利用旋转进行计算或证明 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:15:19 | ||
图片预览



文档简介
(共12张PPT)
类型1利用旋转进行计算
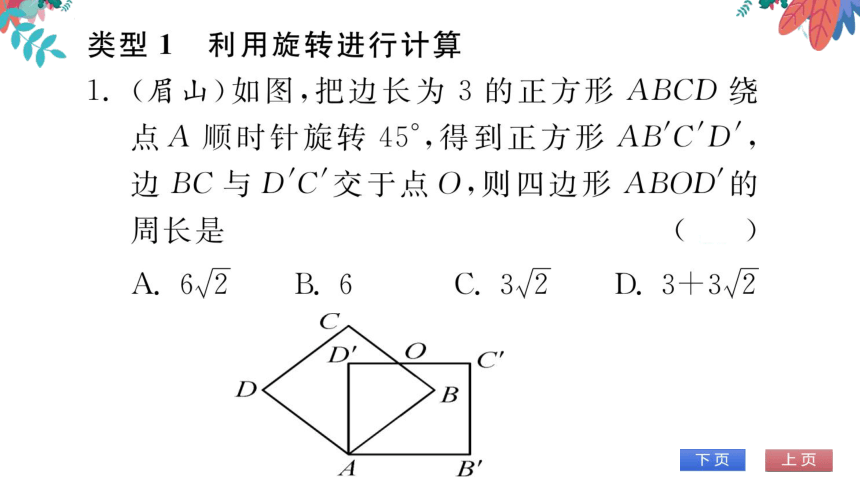
(眉山)如图,把边长为3的正方形ABCD绕
点A顺时针旋转45°,得到正方形AB'CD′,
边BC与DC交于点O,则四边形ABOD的
周长是
(A)
A.6√2
D
B
B
(第1题图
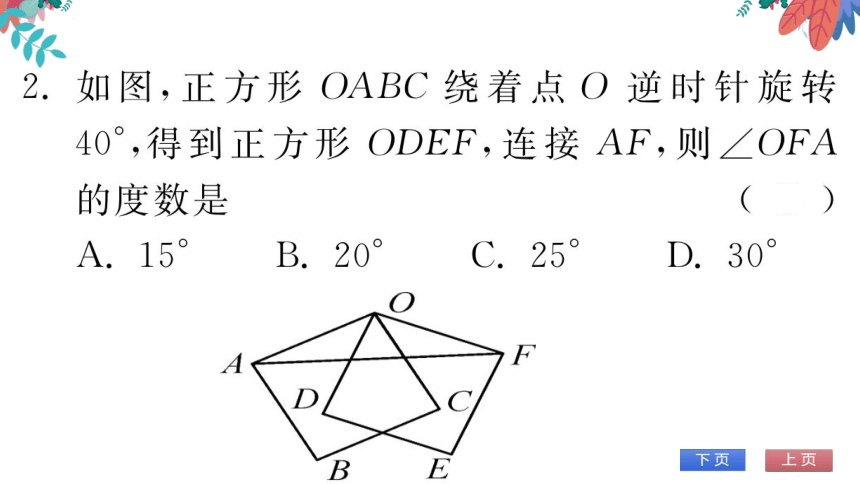
如图,正方形OABC绕着点O逆时针旋转
40°,得到正方形ODEF,连接AF,则∠OFA
的度数是
B.20
D.30
D
B
E
(第2题图)
如图,在Rt△ABC中,∠ACB=90°,∠B
60°,BC=2,△DEC是由△ABC绕点C顺时
针旋转得到的,连接AD,若A,E,D在同一直
线上,则AD的长为
A.6
B.4
C.4√3
E
C
B
第3题图
4.如图,在△ABC中,∠A=70°,AC=BC,以点
B为旋转中心,把△ABC顺时针旋转α角,得
到△A'BC,点A恰好落在AC边上,连接
CC,则∠ACC的度数是110
B
C
C
(第4题图
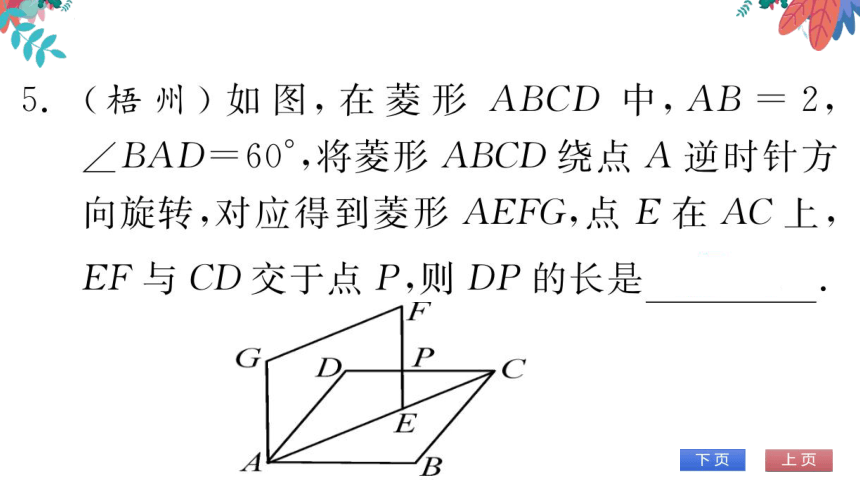
(梧州)如图,在菱形ABCD中,AB=2,
∠BAD=60°,将菱形ABCD绕点A逆时针方
向旋转,对应得到菱形AEFG,点E在AC上
EF与CD交于点P,则DP的长是3-1
类型2利用旋转进行证明
(娄底)如图,将等腰△ABC绕顶点B按逆时
针方向旋转α角到△A1BC1的位置,AB与
A1C1相交于点D,AC与A1C1,BC1分别交于
点E,F.
1)求证:BCF≌△BA1D
1)证明:△ABC是等腰三角形
AB=BC,∠A=∠
由题意及旋转的性质知
A1B=AB=BC,∠A1=∠A
ABa
CBO
在△BCF和△BA1D中,A1B=CB
∠ABA1=∠CBC1
△BCF≌△BA1D(AAS)
2)解:四边形A1BCE为菱形,理由如下:
由(1)知∠A=∠A1=∠C=∠C1,
当∠C=a时,则∠A=∠C
又∠ABA
CBC=a
∠A=∠ABA1,∠C
CBO
(南充)如图,在矩形ABCD中,AC=2AB,将
矩形ABCD绕点A旋转得到矩形AB'C'D′,
使点B的对应点B落在AC上,BC交AD于
点E,在BC上取点F,使BF=AB
(1)求证:AE=CE;
(2)求∠FBB的度数;
(3)已知AB=2,求BF的长
D
B
)证明:∵四边形ABCD是矩形,
△ABC是直角三角形
AC=2AB,矩形ABCD′是由矩形
ABCD旋转得到的,
AB
AC.∴.BB
Ac
AB=AB=BB,△ABB是等边三角形.∴∠ACB
DAC=∠DAC=30°
CAD=∠ACB.∴AE=CE
2)解:∵△ABB是等边三角形,
∠ABB=60,AB=BB
又∠ABC=90°,∴∠BB'F=90°+60°=150°
BF=AB=BB,∴∠FBB=∠BFB=15°
(3)解:过点F作FH⊥BB交BB的延长线于点H
∠FBH=30°,由(2)知BF=BB=AB=2
FH=1.∴BH=√BF-FH
类型1利用旋转进行计算
(眉山)如图,把边长为3的正方形ABCD绕
点A顺时针旋转45°,得到正方形AB'CD′,
边BC与DC交于点O,则四边形ABOD的
周长是
(A)
A.6√2
D
B
B
(第1题图
如图,正方形OABC绕着点O逆时针旋转
40°,得到正方形ODEF,连接AF,则∠OFA
的度数是
B.20
D.30
D
B
E
(第2题图)
如图,在Rt△ABC中,∠ACB=90°,∠B
60°,BC=2,△DEC是由△ABC绕点C顺时
针旋转得到的,连接AD,若A,E,D在同一直
线上,则AD的长为
A.6
B.4
C.4√3
E
C
B
第3题图
4.如图,在△ABC中,∠A=70°,AC=BC,以点
B为旋转中心,把△ABC顺时针旋转α角,得
到△A'BC,点A恰好落在AC边上,连接
CC,则∠ACC的度数是110
B
C
C
(第4题图
(梧州)如图,在菱形ABCD中,AB=2,
∠BAD=60°,将菱形ABCD绕点A逆时针方
向旋转,对应得到菱形AEFG,点E在AC上
EF与CD交于点P,则DP的长是3-1
类型2利用旋转进行证明
(娄底)如图,将等腰△ABC绕顶点B按逆时
针方向旋转α角到△A1BC1的位置,AB与
A1C1相交于点D,AC与A1C1,BC1分别交于
点E,F.
1)求证:BCF≌△BA1D
1)证明:△ABC是等腰三角形
AB=BC,∠A=∠
由题意及旋转的性质知
A1B=AB=BC,∠A1=∠A
ABa
CBO
在△BCF和△BA1D中,A1B=CB
∠ABA1=∠CBC1
△BCF≌△BA1D(AAS)
2)解:四边形A1BCE为菱形,理由如下:
由(1)知∠A=∠A1=∠C=∠C1,
当∠C=a时,则∠A=∠C
又∠ABA
CBC=a
∠A=∠ABA1,∠C
CBO
(南充)如图,在矩形ABCD中,AC=2AB,将
矩形ABCD绕点A旋转得到矩形AB'C'D′,
使点B的对应点B落在AC上,BC交AD于
点E,在BC上取点F,使BF=AB
(1)求证:AE=CE;
(2)求∠FBB的度数;
(3)已知AB=2,求BF的长
D
B
)证明:∵四边形ABCD是矩形,
△ABC是直角三角形
AC=2AB,矩形ABCD′是由矩形
ABCD旋转得到的,
AB
AC.∴.BB
Ac
AB=AB=BB,△ABB是等边三角形.∴∠ACB
DAC=∠DAC=30°
CAD=∠ACB.∴AE=CE
2)解:∵△ABB是等边三角形,
∠ABB=60,AB=BB
又∠ABC=90°,∴∠BB'F=90°+60°=150°
BF=AB=BB,∴∠FBB=∠BFB=15°
(3)解:过点F作FH⊥BB交BB的延长线于点H
∠FBH=30°,由(2)知BF=BB=AB=2
FH=1.∴BH=√BF-FH
同课章节目录
