21.2 第2课时 用配方法解一元二次方程 习题课件
文档属性
| 名称 | 21.2 第2课时 用配方法解一元二次方程 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:15:19 | ||
图片预览





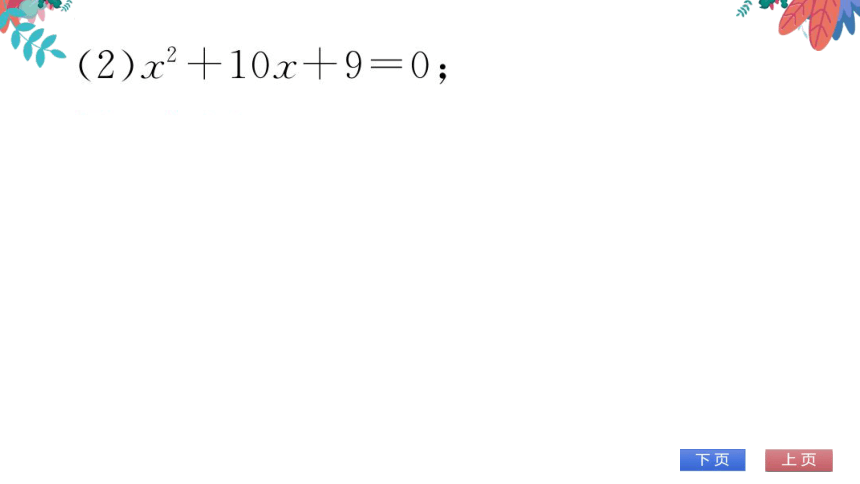
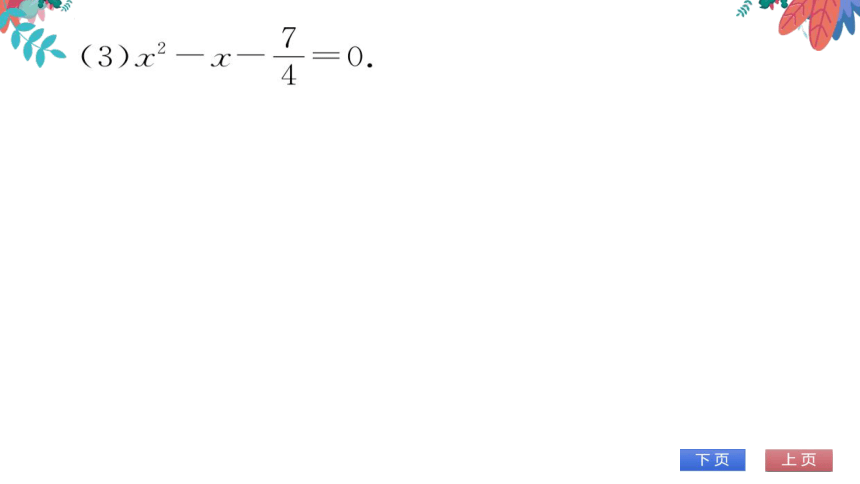
文档简介
(共18张PPT)
知识要点全练
夯奧基础
知识点1完全平方式及配方
1.若代数式x2+ax+16是一个完全平方式,则
a的值是
B.8
C.土4
D.+8
把一元二次方程x2-6x=7配方,则需要在方
程两边都加上
用适当的数填空:
(1)x2+6x
(2)x
知识点2用配方法解二次项系数为1的一元二
次方程
4.用配方法解方程x2+x=1时,方程左右两边
应同时加上
B.1
4
用配方法解一元二次方程x2-4x-1=0,下
列变形正确的是
A.(x-4)
1+4B.(x-4)2=1+4
+2)2=1+4
D.(x-2)2=1+4
用配方法解下列方程
(1
)x2+2x-99=0;
解:x2+2x=99
配方,得x2+2x+1=99+1
即(x+1)2=100,
x+1=±10
11
(2)x2+10x+9=0
解:x2+10x=-9
配方,得x2+10x+25=-9+25
即(x+5)2=16
x+5
4.
(3)x
O
解
474
配方,得x2-x
4
+
知识点3用配方法解二次项系数不为1的一元
二次方程
7.用配方法解方程2x2-x-6=0,开始出现错
误的步骤是
尤
3
4
8.把方程x2-3x-5=0化成(x+m)2=n的
形式是
19
4
用配方法解下列方程
(1)2x2+7x-4=0;
解
9.2
4
规律方法全练
提升能力
10.若9x2+kx+1为完全平方式,则k的值为
11.(2020泰安)将一元二次方程x2-8x-5=0
化成(x+a)2=b(a,b为常数)的形式,则a,b
的值分别是
4,21
4,11
C.4,21
8,6
2.三角形两边的长分别是3和4,第三边的长是
方程x2-12x+35=0的根,则该三角形的周
长为
B
A.14
B.12
C.12或14
D.以上都不对
3.若a2+b2-2a+4b+5=0,则a+b的值为
4.(湛江)若4x2-ax+1=0可配方为(2x6)2=C
的形式,则b
5.(益阳)规定:a∞b=(a+b)b,如:23=(2
3)×3=15.若2x=3,则x=1或-3
6.已知关于x的方程x2+4x+n=0可以配方
成(x+m)2=3,则(m-1)2021=1
若方程2x2-4x-10=0能配成(x+p)2
的形式,则直线y=px+q不经过第三
象限
9.用配方法说明代数式x2—8x+17的值大于
0,再求出当x为何值时,这个代数式的值最
小,最小值是多少
解:x2-8x+17=(x2-8x+16)-16+17
(x-4)2+1
(x-4)2≥0,
(x-4)2+1≥1,即x2-8x+17的值大
于0
当x-4=0,即x=4时,这个代数式的值最
最小值为1
知识要点全练
夯奧基础
知识点1完全平方式及配方
1.若代数式x2+ax+16是一个完全平方式,则
a的值是
B.8
C.土4
D.+8
把一元二次方程x2-6x=7配方,则需要在方
程两边都加上
用适当的数填空:
(1)x2+6x
(2)x
知识点2用配方法解二次项系数为1的一元二
次方程
4.用配方法解方程x2+x=1时,方程左右两边
应同时加上
B.1
4
用配方法解一元二次方程x2-4x-1=0,下
列变形正确的是
A.(x-4)
1+4B.(x-4)2=1+4
+2)2=1+4
D.(x-2)2=1+4
用配方法解下列方程
(1
)x2+2x-99=0;
解:x2+2x=99
配方,得x2+2x+1=99+1
即(x+1)2=100,
x+1=±10
11
(2)x2+10x+9=0
解:x2+10x=-9
配方,得x2+10x+25=-9+25
即(x+5)2=16
x+5
4.
(3)x
O
解
474
配方,得x2-x
4
+
知识点3用配方法解二次项系数不为1的一元
二次方程
7.用配方法解方程2x2-x-6=0,开始出现错
误的步骤是
尤
3
4
8.把方程x2-3x-5=0化成(x+m)2=n的
形式是
19
4
用配方法解下列方程
(1)2x2+7x-4=0;
解
9.2
4
规律方法全练
提升能力
10.若9x2+kx+1为完全平方式,则k的值为
11.(2020泰安)将一元二次方程x2-8x-5=0
化成(x+a)2=b(a,b为常数)的形式,则a,b
的值分别是
4,21
4,11
C.4,21
8,6
2.三角形两边的长分别是3和4,第三边的长是
方程x2-12x+35=0的根,则该三角形的周
长为
B
A.14
B.12
C.12或14
D.以上都不对
3.若a2+b2-2a+4b+5=0,则a+b的值为
4.(湛江)若4x2-ax+1=0可配方为(2x6)2=C
的形式,则b
5.(益阳)规定:a∞b=(a+b)b,如:23=(2
3)×3=15.若2x=3,则x=1或-3
6.已知关于x的方程x2+4x+n=0可以配方
成(x+m)2=3,则(m-1)2021=1
若方程2x2-4x-10=0能配成(x+p)2
的形式,则直线y=px+q不经过第三
象限
9.用配方法说明代数式x2—8x+17的值大于
0,再求出当x为何值时,这个代数式的值最
小,最小值是多少
解:x2-8x+17=(x2-8x+16)-16+17
(x-4)2+1
(x-4)2≥0,
(x-4)2+1≥1,即x2-8x+17的值大
于0
当x-4=0,即x=4时,这个代数式的值最
最小值为1
同课章节目录
