22.2 二次函数与一元二次方程 习题课件
文档属性
| 名称 | 22.2 二次函数与一元二次方程 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:15:19 | ||
图片预览







文档简介
(共24张PPT)
知识要点全练
夯奥基础
知识点1二次函数与一元二次方程
1.如图,已知抛物线y=ax2+bx+c与x轴的一个
交点A(1,0),对称轴为直线x
bx+c=0的解是
a)
X
A
(苏州)若二次函数y=ax2+1的图象经过点
(-2,0),则关于x的方程a(x-2)2+1=0的
实数根是
A.x1=0,
4
4,x,=0
3.已知一元二次方程x2-3x+2=0有两个不相等
的实数根为x1=1,x2=2,则二次函数y=x2
3x+2与x轴的交点坐标为(1,0),(2,0)
4.以抛物线y=-x2-x+6与坐标轴的三个交
点为顶点的三角形的面积为15
知识点2抛物线与x轴的交点个数对应一元二
次方程根的情况
(襄阳)已知二次函数y=x2-1
图象与x轴有交点,则m的取值范围是(A
(荆门)抛物线
x2+4x-4与坐标轴的交
点个数为
B.1
D.3
抛物线y=x2-2x+2-a与x轴有两个不同
的交点,则直线y=ax+a不经过第四
象限
8.若函数y=mx21+2x-1的图象与x轴只有
个交点,则实数m的值为0或-1
知识点3利用函数的图象求一元二次方程的近
似根
(兰州)下表是一组二次函数y=x2+3x-5的
自变量x与函数值y的对应值:
1.4
0.490.04
o 5g
那么方程x2+3x-5=0的一个近似根是
B.
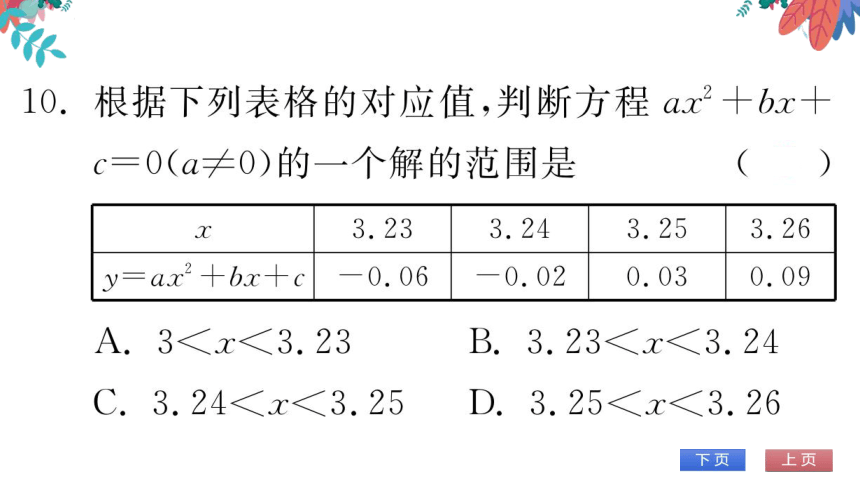
0.根据下列表格的对应值,判断方程ax2+bx
c=0(a≠0)的一个解的范围是
3.23
3.24
3.25
3.26
y-a.
bx
0.06
0.02
0.03
0.09
23
2324知识点4二次函数与一元二次不等式
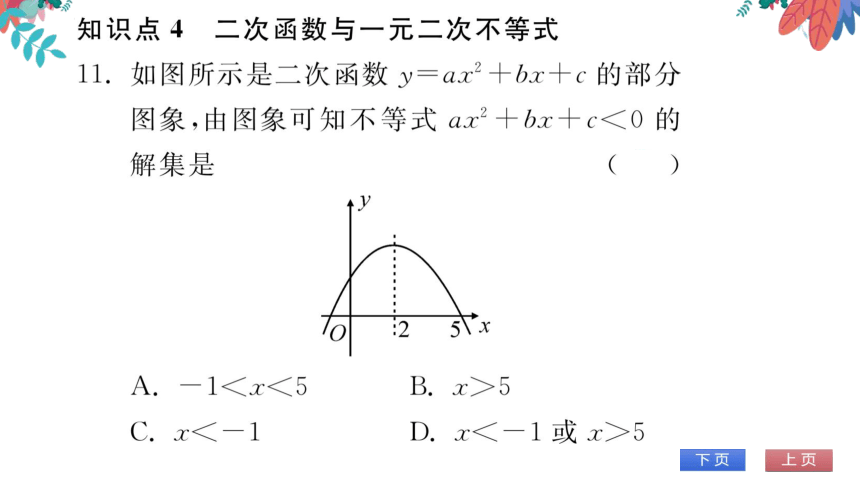
11.如图所示是二次函数y=ax2+bx+c的部分
图象,由图象可知不等式ax2+bx+c<0的
解集是
25
A.—1B.x>5
1或x>5
2.二次函数y=ax2+bx+c的图象如图所示,
根据图象解答下列问题:
/123x
(1)方程ax+bx+c=0的解为x1=1,x2=3;
(2)不等式ax2+bx+C>0的解集为1~x3;
(3)y随x的增大而减小的自变量x的取值
范围为x>2;
规律方法全练
提升能力
13.(宿迁)若二次函数y=ax2-2ax+c的图象
经过点(-1,0),则方程ax2-2ax+c=0的
解是
912
4.二次函数y=a(x-4)2-4(a≠0)的图象在
2这一段位于x轴的上方,则a的值为(A
知识要点全练
夯奥基础
知识点1二次函数与一元二次方程
1.如图,已知抛物线y=ax2+bx+c与x轴的一个
交点A(1,0),对称轴为直线x
bx+c=0的解是
a)
X
A
(苏州)若二次函数y=ax2+1的图象经过点
(-2,0),则关于x的方程a(x-2)2+1=0的
实数根是
A.x1=0,
4
4,x,=0
3.已知一元二次方程x2-3x+2=0有两个不相等
的实数根为x1=1,x2=2,则二次函数y=x2
3x+2与x轴的交点坐标为(1,0),(2,0)
4.以抛物线y=-x2-x+6与坐标轴的三个交
点为顶点的三角形的面积为15
知识点2抛物线与x轴的交点个数对应一元二
次方程根的情况
(襄阳)已知二次函数y=x2-1
图象与x轴有交点,则m的取值范围是(A
(荆门)抛物线
x2+4x-4与坐标轴的交
点个数为
B.1
D.3
抛物线y=x2-2x+2-a与x轴有两个不同
的交点,则直线y=ax+a不经过第四
象限
8.若函数y=mx21+2x-1的图象与x轴只有
个交点,则实数m的值为0或-1
知识点3利用函数的图象求一元二次方程的近
似根
(兰州)下表是一组二次函数y=x2+3x-5的
自变量x与函数值y的对应值:
1.4
0.490.04
o 5g
那么方程x2+3x-5=0的一个近似根是
B.
0.根据下列表格的对应值,判断方程ax2+bx
c=0(a≠0)的一个解的范围是
3.23
3.24
3.25
3.26
y-a.
bx
0.06
0.02
0.03
0.09
23
23
11.如图所示是二次函数y=ax2+bx+c的部分
图象,由图象可知不等式ax2+bx+c<0的
解集是
25
A.—1
1或x>5
2.二次函数y=ax2+bx+c的图象如图所示,
根据图象解答下列问题:
/123x
(1)方程ax+bx+c=0的解为x1=1,x2=3;
(2)不等式ax2+bx+C>0的解集为1~x3;
(3)y随x的增大而减小的自变量x的取值
范围为x>2;
规律方法全练
提升能力
13.(宿迁)若二次函数y=ax2-2ax+c的图象
经过点(-1,0),则方程ax2-2ax+c=0的
解是
912
4.二次函数y=a(x-4)2-4(a≠0)的图象在
2
同课章节目录
