22.3 第二课时 建立适当的直角坐标系解决实际问题 习题课件
文档属性
| 名称 | 22.3 第二课时 建立适当的直角坐标系解决实际问题 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:15:19 | ||
图片预览






文档简介
(共22张PPT)
知识要点全练
夯奧基础
知识点1用二次函数解决拱桥类问题
赵州桥的桥拱是近似的抛物线形,建立如图所示
的平面直角坐标系,其函数解析式为
25
当水面离桥拱顶的高度OD是4m时,这时水面
的宽度AB为
20mB.10
C.20
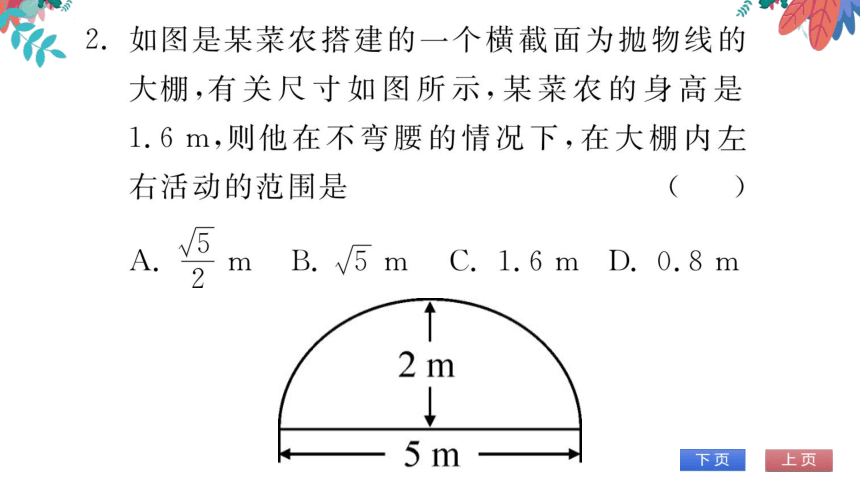
如图是某菜农搭建的一个横截面为抛物线的
大棚,有关尺寸如图所示,某菜农的身高是
1.6m,则他在不弯腰的情况下,在大棚内左
右活动的范围是
B
A.y。mB.√5mC.1.6mD.0.8m
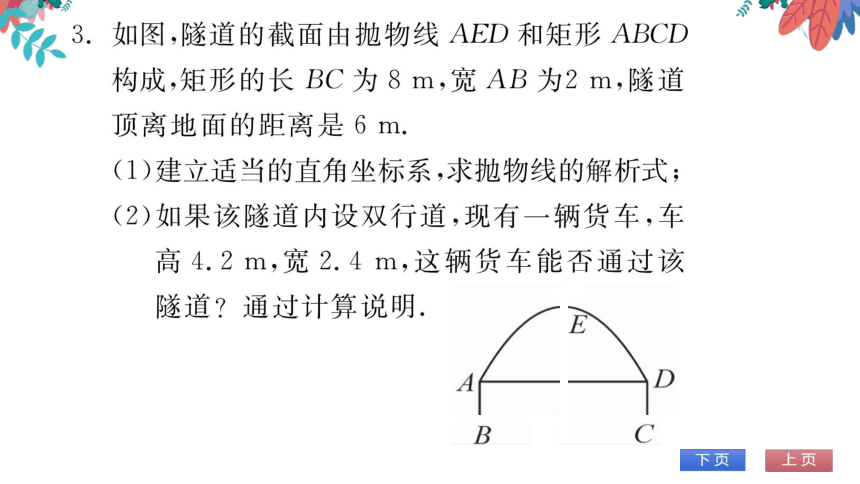
如图,隧道的截面由抛物线AED和矩形ABCD
构成,矩形的长BC为8m,宽AB为2m,隧道
顶离地面的距离是6m
(1)建立适当的直角坐标系,求抛物线的解析式
(2)如果该隧道内设双行道,现有一辆货车,车
高4.2m,宽2.4m,这辆货车能否通过该
隊道 通过计算说明
解:(1)设BC所在直线为x
轴,线段BC的中垂线为y轴
建立平面直角坐标系,如图
依题意,得抛物线的顶点
E(0,6),D(4,2)
于是设抛物线的解析式为y=ax2+6,
把(4,2)代入得16a+6=2,∴a
4
4
(2)当x=2.4时,y
6=4.56>4.2
4
故这辆货车能通过该隧道
知识点2用二次函数知识解决运动问题
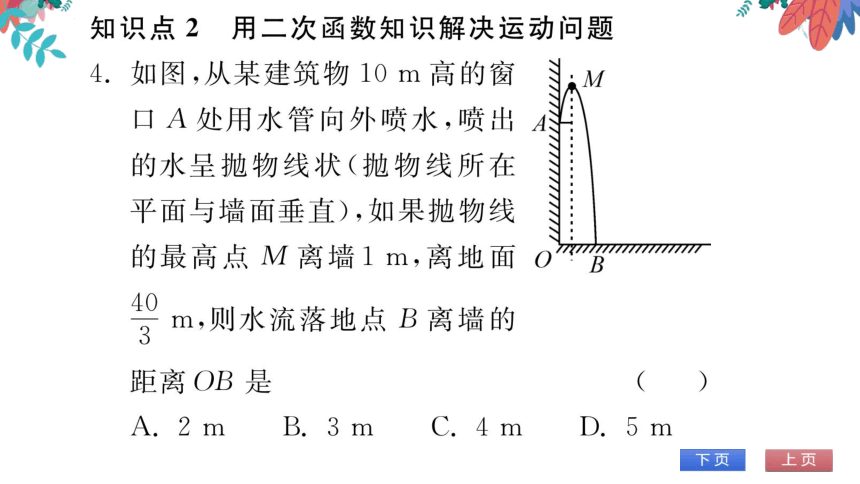
4.如图,从某建筑物10m高的窗
A处用水管向外喷水,喷出
的水呈抛物线状(抛物线所在
平面与墙面垂直),如果抛物线
的最高点M离墙1m,离地面omB
40
3m,则水流落地点B离墙的
距离OB是
B
B.3 m
C.4
飞机着陆后滑行的距离s(单位:m)关于滑行
的时间t(单位:s)的函数解析式是s=60t
2,则飞机着陆后最后10s滑行的距离是
150m
(滨州)如图,一小球沿与地面成一定角度的方
向飞出,小球的飞行路线是一条抛物线.如果
不考虑空气阻力,小球的飞行高度y(单位:m)
与飞行时间x(单位:s)之间具有函数关系y
5x2+20x,请根据要求解答下列问题
(1)在飞行过程中,当小球的飞行高度为15m
时,行时间是多少
(2)在飞行过程中,小球从飞出到落地所用时
间是多少
答:在飞行过程中,当小球的飞行高度为15m
时,飞行时间是1s或3
(2)当y=0时,0=-5x2+20x,
解得x1=0,x2=4.∵4-0=4,∴在飞行过程
中,小球从飞出到落地所用时间是4s
(3)
5x2+20x=-5(x-2)2+20
当x=2时,y取得最大值,y最大=20
答:在飞行过程中,第2s时小球飞行高度最
大,最大高度是20m
知识要点全练
夯奧基础
知识点1用二次函数解决拱桥类问题
赵州桥的桥拱是近似的抛物线形,建立如图所示
的平面直角坐标系,其函数解析式为
25
当水面离桥拱顶的高度OD是4m时,这时水面
的宽度AB为
20mB.10
C.20
如图是某菜农搭建的一个横截面为抛物线的
大棚,有关尺寸如图所示,某菜农的身高是
1.6m,则他在不弯腰的情况下,在大棚内左
右活动的范围是
B
A.y。mB.√5mC.1.6mD.0.8m
如图,隧道的截面由抛物线AED和矩形ABCD
构成,矩形的长BC为8m,宽AB为2m,隧道
顶离地面的距离是6m
(1)建立适当的直角坐标系,求抛物线的解析式
(2)如果该隧道内设双行道,现有一辆货车,车
高4.2m,宽2.4m,这辆货车能否通过该
隊道 通过计算说明
解:(1)设BC所在直线为x
轴,线段BC的中垂线为y轴
建立平面直角坐标系,如图
依题意,得抛物线的顶点
E(0,6),D(4,2)
于是设抛物线的解析式为y=ax2+6,
把(4,2)代入得16a+6=2,∴a
4
4
(2)当x=2.4时,y
6=4.56>4.2
4
故这辆货车能通过该隧道
知识点2用二次函数知识解决运动问题
4.如图,从某建筑物10m高的窗
A处用水管向外喷水,喷出
的水呈抛物线状(抛物线所在
平面与墙面垂直),如果抛物线
的最高点M离墙1m,离地面omB
40
3m,则水流落地点B离墙的
距离OB是
B
B.3 m
C.4
飞机着陆后滑行的距离s(单位:m)关于滑行
的时间t(单位:s)的函数解析式是s=60t
2,则飞机着陆后最后10s滑行的距离是
150m
(滨州)如图,一小球沿与地面成一定角度的方
向飞出,小球的飞行路线是一条抛物线.如果
不考虑空气阻力,小球的飞行高度y(单位:m)
与飞行时间x(单位:s)之间具有函数关系y
5x2+20x,请根据要求解答下列问题
(1)在飞行过程中,当小球的飞行高度为15m
时,行时间是多少
(2)在飞行过程中,小球从飞出到落地所用时
间是多少
答:在飞行过程中,当小球的飞行高度为15m
时,飞行时间是1s或3
(2)当y=0时,0=-5x2+20x,
解得x1=0,x2=4.∵4-0=4,∴在飞行过程
中,小球从飞出到落地所用时间是4s
(3)
5x2+20x=-5(x-2)2+20
当x=2时,y取得最大值,y最大=20
答:在飞行过程中,第2s时小球飞行高度最
大,最大高度是20m
同课章节目录
