22.3 第一课时 几何图形面积及利润问题 习题课件
文档属性
| 名称 | 22.3 第一课时 几何图形面积及利润问题 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:15:19 | ||
图片预览








文档简介
(共22张PPT)
知识要点全练
夯奧基础
知识点1几何图形面积与二次函数
1.如图,假设篱笆(虚线部分)的长度是16m,则
所围成矩形ABCD的最大面积是
A.60m2
B.63m2
64
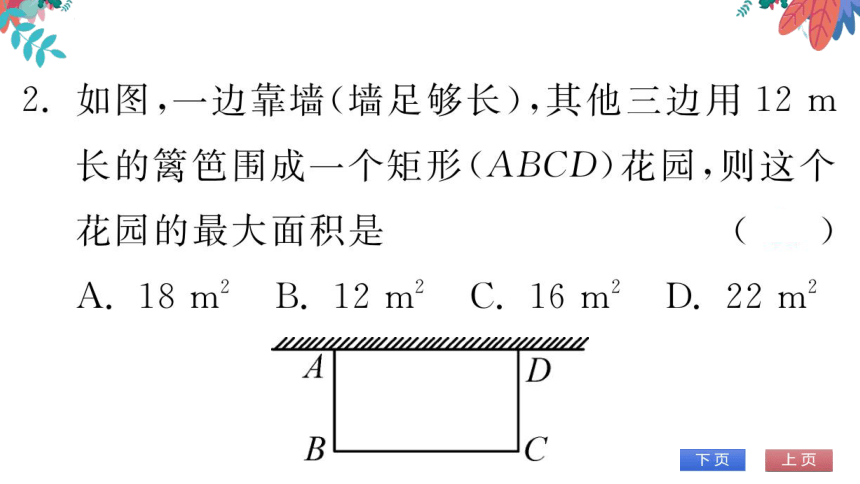
如图,一边靠墙(墙足够长),其他三边用12m
长的篱笆围成一个矩形(ABCD)花园,则这个
花园的最大面积是
图,已知ABCD的周长为8cm,∠B
30°,若边长AB=xcm
(1)□ABCD的面积y(单位:cm2)与x(单位:cm
之间的函数解析式为y
2x,自
变量x的取值范围是0(2)当x取2时,y的值最大,最大值为2
4.(沈阳)如图,一块矩形土地ABCD由篱笆围
着,并且由一条与C边平行的篱笆EF分
开.已知篱笆的总长为900m(篱笆的厚度忽
略不计),当AB
150m时,矩形土地
ABCD的面积最大
E
B
C
(第4题图)
知识点2利润问题与二次函数
服装店将进价为100元/件的服装按x元/件
出售,每天可销售(200-x)件,若想获得最大
利润,则x应定为
A.150元B.160元
170元D.180元
有一家80间套房的旅馆,经调查得知,若把每
日租金定价为160元,则可客满,而租金每涨
20元,就会失去3位客人,每间住了人的客房
每所需服务、维修等各项支出共计40元,赚
钱最多时定价为
A.160元
B.240元
C.360元
D.450元
7.某商品的利润y(单位:元)与售价x(单位:元
之间的函数关系式是
x2+8x+9,且售
价x的取值范围是1≤x≤3,则可获得的最大
利润是24元
(济宁)某商店经销一种双肩包,已知这种双肩
包的成本价为每个30元,市场调查发现,这种
双肩包每天的销售量y(单位:个)与销售单价
x(单位:元)有如下关系:y
x+60(30
x≤60).设这种双肩包每天的销售利润为
1)求W与x之间的函数解析式;
2)这种双肩包销售单价定为多少元时,每天
的销售利润最大 最大利润是多少元
3)如果物价部门规定这种双肩包的销售单价
不高于48元,该商店销售这种双肩包每天
要获得200元的销售利润,销售单价应定
为多少元
解:(1)W=(x-30)y=(x-30)(-x+60),
x2+90x-1800(30≤x≤60)
(2)W
90x-1800
(x-45)2+225
当x=45时,W最大为225,即销售单价定
为45元时,每天获利最大为225元
知识要点全练
夯奧基础
知识点1几何图形面积与二次函数
1.如图,假设篱笆(虚线部分)的长度是16m,则
所围成矩形ABCD的最大面积是
A.60m2
B.63m2
64
如图,一边靠墙(墙足够长),其他三边用12m
长的篱笆围成一个矩形(ABCD)花园,则这个
花园的最大面积是
图,已知ABCD的周长为8cm,∠B
30°,若边长AB=xcm
(1)□ABCD的面积y(单位:cm2)与x(单位:cm
之间的函数解析式为y
2x,自
变量x的取值范围是0
4.(沈阳)如图,一块矩形土地ABCD由篱笆围
着,并且由一条与C边平行的篱笆EF分
开.已知篱笆的总长为900m(篱笆的厚度忽
略不计),当AB
150m时,矩形土地
ABCD的面积最大
E
B
C
(第4题图)
知识点2利润问题与二次函数
服装店将进价为100元/件的服装按x元/件
出售,每天可销售(200-x)件,若想获得最大
利润,则x应定为
A.150元B.160元
170元D.180元
有一家80间套房的旅馆,经调查得知,若把每
日租金定价为160元,则可客满,而租金每涨
20元,就会失去3位客人,每间住了人的客房
每所需服务、维修等各项支出共计40元,赚
钱最多时定价为
A.160元
B.240元
C.360元
D.450元
7.某商品的利润y(单位:元)与售价x(单位:元
之间的函数关系式是
x2+8x+9,且售
价x的取值范围是1≤x≤3,则可获得的最大
利润是24元
(济宁)某商店经销一种双肩包,已知这种双肩
包的成本价为每个30元,市场调查发现,这种
双肩包每天的销售量y(单位:个)与销售单价
x(单位:元)有如下关系:y
x+60(30
x≤60).设这种双肩包每天的销售利润为
1)求W与x之间的函数解析式;
2)这种双肩包销售单价定为多少元时,每天
的销售利润最大 最大利润是多少元
3)如果物价部门规定这种双肩包的销售单价
不高于48元,该商店销售这种双肩包每天
要获得200元的销售利润,销售单价应定
为多少元
解:(1)W=(x-30)y=(x-30)(-x+60),
x2+90x-1800(30≤x≤60)
(2)W
90x-1800
(x-45)2+225
当x=45时,W最大为225,即销售单价定
为45元时,每天获利最大为225元
同课章节目录
