24.1.2 垂直于弦的直径　习题课件

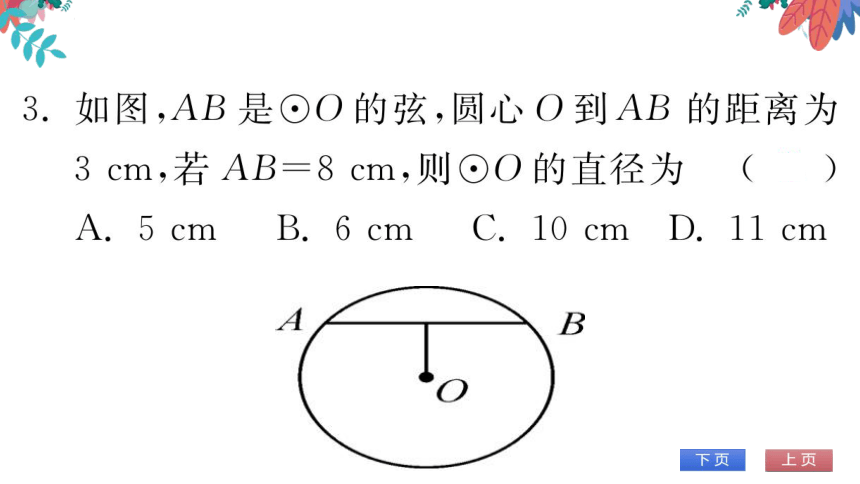
(共26张PPT)
知识要点全练
夯奧基础
知识点1圆的轴对称性
1.下列说法中,不正确的有
B
①圆是轴对称图形,它有无数条对称轴;②直
径是圆的对称轴;③经过圆心的直线是圆的对
称轴;④圆绕着它的圆心旋转任意角度,都能
与它自身重合
D.4个
知识点2垂径定理及其推论
如图,AB是⊙O的直径,弦CD⊥AB,垂足为
M,下列结论不正确的是
A CM=DM
B. CB- BD
C.∠ACD=∠ADCD.OM=MB
O
B
第2题图)
CEO
B
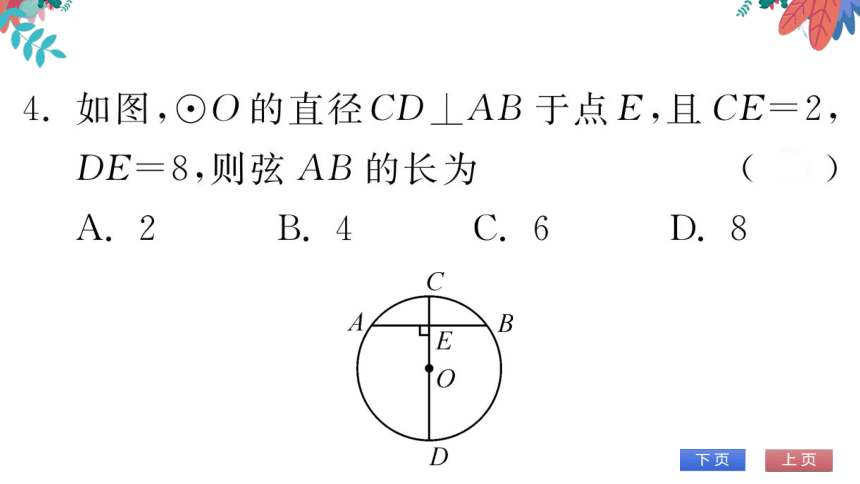
(第4题图)
(2020滨州)在⊙O中,直径AB=15,弦DE⊥AB
于点C,若OC:OB=3:5,则DE的长为12
7.(2020陕西)如图,△ABC的三个顶点都在⊙O
上,∠A=50°,E是边BC的中点,连接OE并延
长,交⊙O于点D,连接BD,则∠D的大小为
65
B
D
(第7题图)
知识点3垂径定理的实际应用
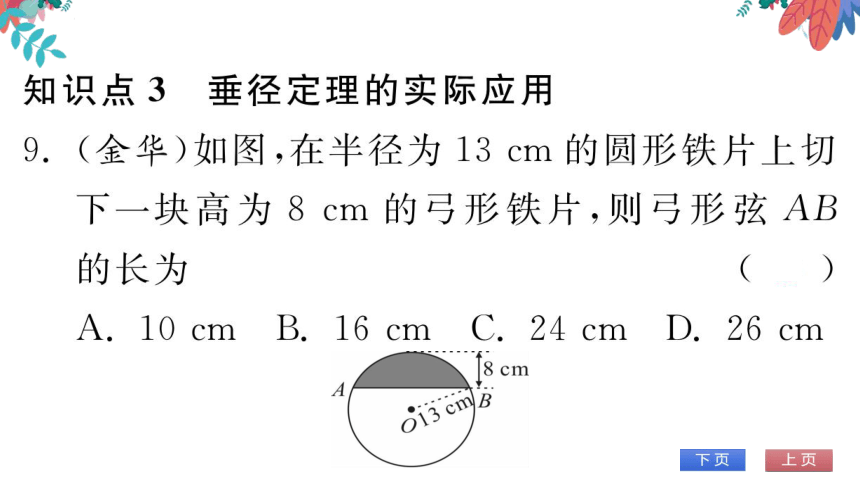
9.(金华)如图,在半径为13cm的圆形铁片上切
下一块高为8cm的弓形铁片,则弓形弦AB
的长为
a. 10 cm b. 16 cm
24 cm D.26 cm
8 cm
013 cmB
(第9题图
0.如图,将半径为2cm的圆形纸片折叠后,圆
弧恰好经过圆心O,则折痕AB的长为(C
a.2 cm
B.√3cm
C.2√3cm
cm
B
(第10题图)
1.如图,工程上常用钢珠来测量零件上小圆孔
的宽口,假设钢珠的直径是10mm,测得钢珠
顶端离零件表面的距离为8mm,则这个小圆
孔的宽口AB是8mm
8 mm
AD=AB=1(m),∠CDA=90°
设⊙O的半径为R,则
OA=OCEROD=5-R
在Rt△OAD中,由色股定理,得
OA2=OD2+AD2,即
R2=(5-R)2+12,解得R=2.6
故圆拱形门所在圆的半径为2.6m
规律方法全练
提升能力
13.如图,已知⊙O的半径为10,AB⊥CD,垂足
为P,且AB=CD=16,则OP=6√2
B
(第13题图)
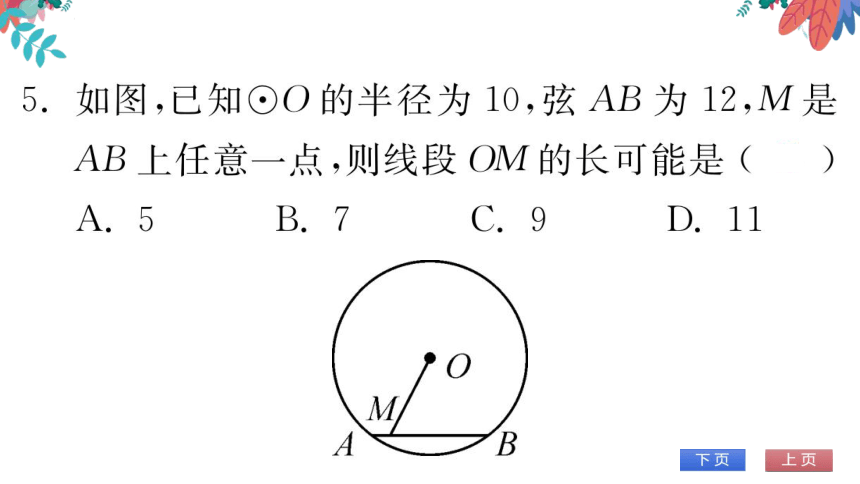
4.如图,点A,B是⊙O上两点,AB=10,点P
是⊙O上的动点(P与A,B不重合),连接
AP,PB,过点O分别作OE⊥AP于点E,
OF⊥PB于点F,则EF
(第14题图)
(第15题图)
6.(易错题)如图,一个下水管道的横截面为圆
形,直径为100cm,下雨前水面宽为60cm,
场大雨过后,水面宽为80cm,则水位上升
10或70cm