24.1.3 弧、弦、圆心角　习题课件

(共27张PPT)
知识要点全练
夯奧基础
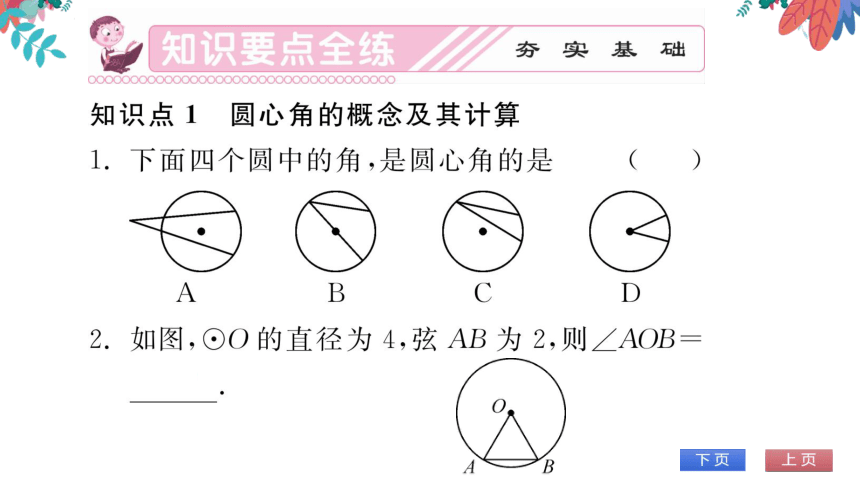
知识点1圆心角的概念及其计算
下面四个圆中的角,是圆心角的是
如图,⊙O的直径为4,弦AB为2,则∠AOB
60°
知识点2弧、弦、圆心角之间的关系
4.在同圆或等圆中,不一定成立的是
A.相等的圆心角所对的弧相等
B.相等的弦所对的弧相等
C.相等的弧所对的圆心角相等
D.相等的弧所对的弦相等
图,∠AOB=∠COD,下列结论不一定成立
的是
A.AB=CD
B. AB=CD
C.△AOB≌△COD
D.△AOB,△COD都是等边三角形
D
B
(第5题图)
B
D
O
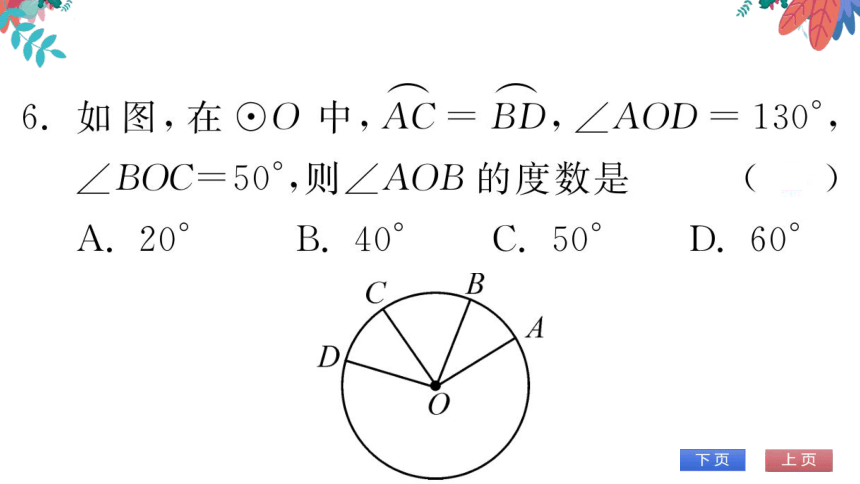
(第6题图)
C B
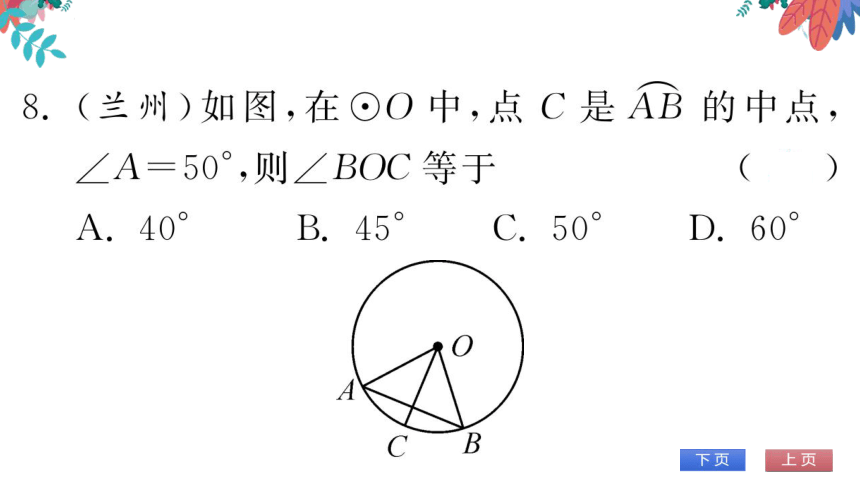
(第8题图)
B
DTE
(第10题图)
证明:连接OC
CD⊥AO,CE⊥OB,
CDO
CEO=90
AC=cB
AOC
EOC
OC公用
CDO△CEO(AAS
规律方法全练
提升能力
13.已知AB,CD是同圆的两段弧,且AB=2CD,
则弦AB与2CD之间的数量关系为(B)
A.=2CD
B. AB<2CD
C. AB2CD
D.不能确定
4.如图,O通过五边形 OABCD的四个顶点.若
ABD所对的圆心角为150°,∠A=75°,∠D
60°,则BC所对的圆心角的度数为
(D)
B.40°
D
B
(第14题图)
5.如图,已知AB和CD是⊙O的两条等弦,
OM⊥AB,ON⊥CD,垂足分别为M,N,BA
与DC的延长线交于点P,连接OP.下列四
个说法:①AB=CD;②OM=ON;③PA=PC
④∠BPO=∠DPO.其中正确的是
A.1个B.2个C.3个D.4个
B M
(第16题图
(德州)如图,CD为⊙O的直径,弦AB⊥CD,
垂足为E,AB=BF,CE=1,AB=6,则弦AF
4
的长度为
EB
(第17题图)
图,AB是⊙O的直径,M,N分别在半径
OA,OB上,且AM=BN,过点M,N作AB
的垂线,分别交⊙O于点C,D.求证
bD
证明:连接OC,OD
OA=OB, AM=BN,
OMEON
CM⊥AB,DN⊥AB
CMO=∠DNO=90°
证明:连接AC,BD
C,D是AB的三等分点,
C AC=CD=BD
AC-BD=CD
1=∠2=∠3=∠AOB
AOb=90,
OA=OC
180°-30
∠OAC=∠ACO
又OA=OB,∠AOB=90
180°-90°
OAB=∠ABO
45
AEC=∠OAB+/1=75
ABC=∠ACE
AE=AC.同理BF=BD,故AE=BF=CD