24.1.4 圆周角 习题课件
图片预览


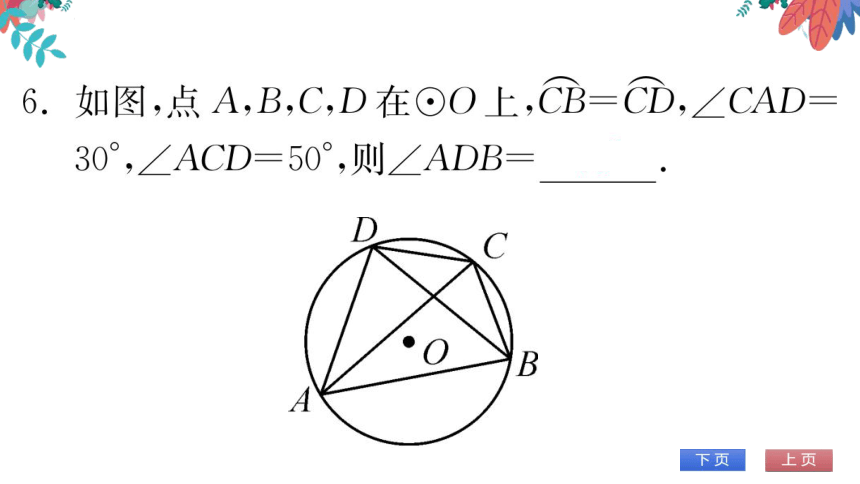
文档简介
(共27张PPT)
知识要点全练
夯奧基础
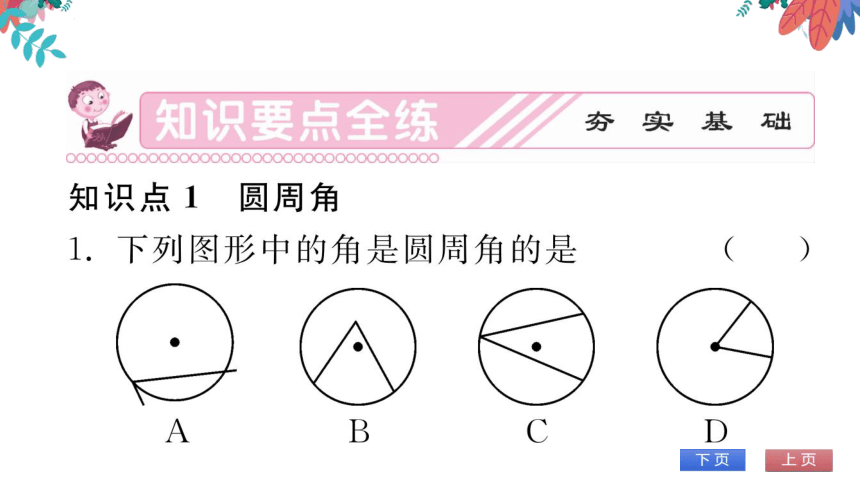
知识点1圆周角
下列图形中的角是圆周角的是
知识点2圆周角定理及其推论
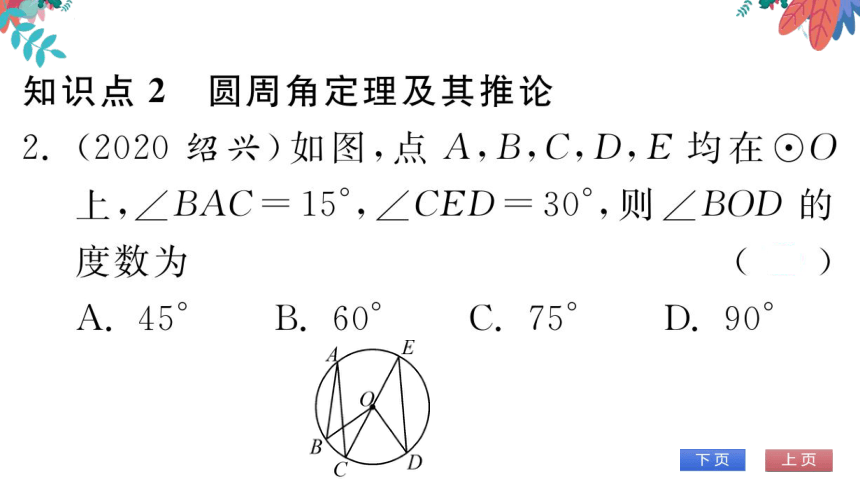
(2020绍兴)如图,点A,B,C,D,E均在⊙O
上,∠BAC=15,∠CED=30°,则∠BOD的
度数为
B.60
D.90
B
(第3题图)
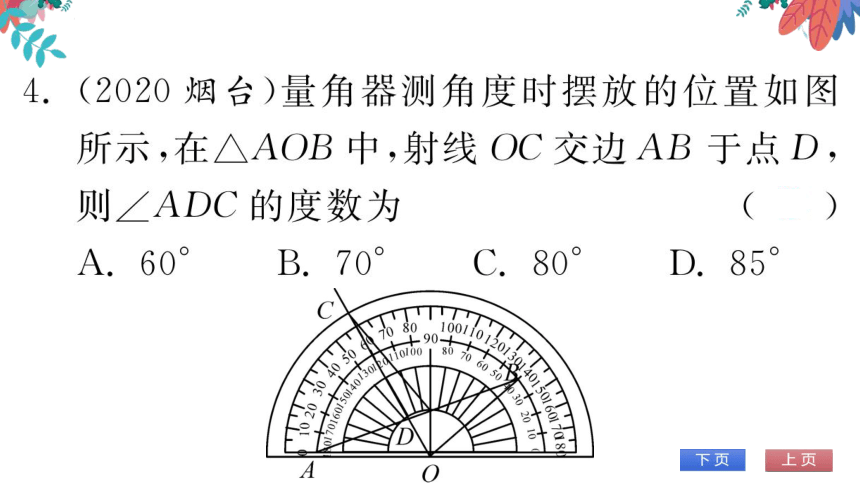
4.(2020烟台)量角器测角度时摆放的位置如图
所示,在△AOB中,射线OC交边AB于点D,
则∠ADC的度数为
A.60
B.70
C.80°
D.85
80100
90
o00
沁N
O
(第4题图
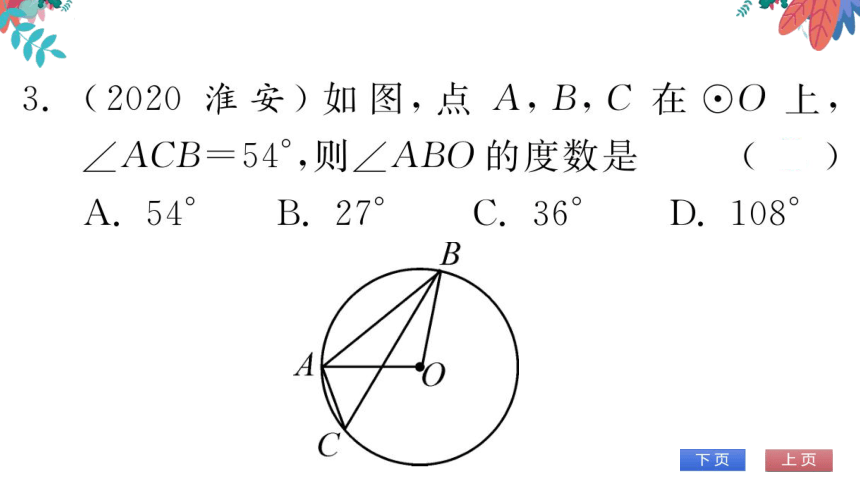
(2020十堰)如图,点A,B,C,D在⊙O上,
OA⊥BC,垂足为E.若∠ADC=30°,AE=1
则BC的长为
A.2
B.4
E
(第5题图)
C
B
(第6题图)
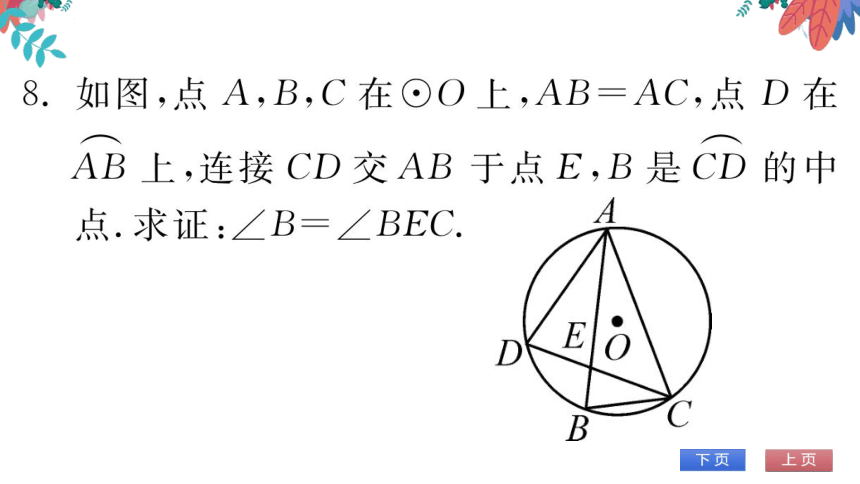
证明:∵B是CD的中点,
BC=BD
∴∠BCE=∠BAC
∠BEC=180—∠B-∠BCE
ACB=180°
B-∠BAC,
∠BEC
ACB
AB=AC,∴∠B=∠ACB
B
BEC
知识点3圆内接四边形
(2020镇江)如图,AB是半圆的直径,C,D是
半圆上的两点,∠ADC=106°,则∠CAB等于
A.10
B.14
C
(第9题图
D
B
(第10题图)
图,四边形ABCD是⊙O的内接四
边形,AD与BC的延长线相交于点E,BA与
CD的延长线相交于点F,∠DCE=80°,
∠F=25°,则∠E的度数为45
E
DACY
O
第12题图)
规律方法全练
提升能力
13.(2020青岛)如图,BD是⊙O的直径,点A,C
在⊙O上,AB=AD,AC交BD于点G.若
COD=126,则∠AGB的度数为
B
B.10
第13题图)
4.如图,BC是半圆O的直径,D,E是BC上的
两点,连接BD,CE,并延长交于点A,连接
OD,OE.如果∠A=70°,那么∠DOE的度数
为
40
D.4
E
B
(第14题图
5.如图,四边形ABCD内接于⊙O,AH⊥BC
交CB的延长线于点H,若BA平分∠DBH,
AD=5,CH=4,则AH等于
H B
(第15题图)
B
(第16题图)
B
(第17题图)
8.如图,AB是⊙O的直径,AB=AC,BC,AC
分别与⊙O相交于点D,E
(1)求证:BD=CD;
(2)若∠BAC=40°,求∠EBC的度数
B D c
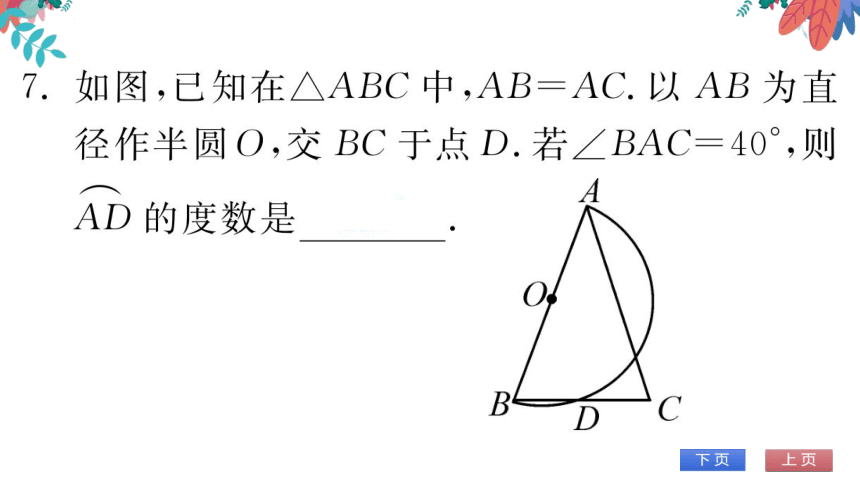
1)证明:连接AD
°AB是⊙O的直径
∴∠ADB=90°.∴AD⊥BC
又AB=AC
BD=CD
2)解:∵AB是⊙O的直径
∠AEB=90
∴∠ABE=90-∠BAC=50
在△ABC中,AB=AC,∠BAC=40
∠ABC=70
EBO
ABc
ABE=20°
知识要点全练
夯奧基础
知识点1圆周角
下列图形中的角是圆周角的是
知识点2圆周角定理及其推论
(2020绍兴)如图,点A,B,C,D,E均在⊙O
上,∠BAC=15,∠CED=30°,则∠BOD的
度数为
B.60
D.90
B
(第3题图)
4.(2020烟台)量角器测角度时摆放的位置如图
所示,在△AOB中,射线OC交边AB于点D,
则∠ADC的度数为
A.60
B.70
C.80°
D.85
80100
90
o00
沁N
O
(第4题图
(2020十堰)如图,点A,B,C,D在⊙O上,
OA⊥BC,垂足为E.若∠ADC=30°,AE=1
则BC的长为
A.2
B.4
E
(第5题图)
C
B
(第6题图)
证明:∵B是CD的中点,
BC=BD
∴∠BCE=∠BAC
∠BEC=180—∠B-∠BCE
ACB=180°
B-∠BAC,
∠BEC
ACB
AB=AC,∴∠B=∠ACB
B
BEC
知识点3圆内接四边形
(2020镇江)如图,AB是半圆的直径,C,D是
半圆上的两点,∠ADC=106°,则∠CAB等于
A.10
B.14
C
(第9题图
D
B
(第10题图)
图,四边形ABCD是⊙O的内接四
边形,AD与BC的延长线相交于点E,BA与
CD的延长线相交于点F,∠DCE=80°,
∠F=25°,则∠E的度数为45
E
DACY
O
第12题图)
规律方法全练
提升能力
13.(2020青岛)如图,BD是⊙O的直径,点A,C
在⊙O上,AB=AD,AC交BD于点G.若
COD=126,则∠AGB的度数为
B
B.10
第13题图)
4.如图,BC是半圆O的直径,D,E是BC上的
两点,连接BD,CE,并延长交于点A,连接
OD,OE.如果∠A=70°,那么∠DOE的度数
为
40
D.4
E
B
(第14题图
5.如图,四边形ABCD内接于⊙O,AH⊥BC
交CB的延长线于点H,若BA平分∠DBH,
AD=5,CH=4,则AH等于
H B
(第15题图)
B
(第16题图)
B
(第17题图)
8.如图,AB是⊙O的直径,AB=AC,BC,AC
分别与⊙O相交于点D,E
(1)求证:BD=CD;
(2)若∠BAC=40°,求∠EBC的度数
B D c
1)证明:连接AD
°AB是⊙O的直径
∴∠ADB=90°.∴AD⊥BC
又AB=AC
BD=CD
2)解:∵AB是⊙O的直径
∠AEB=90
∴∠ABE=90-∠BAC=50
在△ABC中,AB=AC,∠BAC=40
∠ABC=70
EBO
ABc
ABE=20°
同课章节目录
