24.3 正多边形和圆　习题课件

(共22张PPT)
知识要点全练
夯奧基础
知识点1正多边形的有关概念
1.下列命题正确的是
A.各边相等的多边形是正多边形
B.各角相等的多边形是正多边形
C.既是轴对称图形又是中心对称图形的多边
形是正多边形
D.各边相等、各角也相等的多边形是正多边形
对于一个正多边形,下列说法错误的是(B
A.正多边形是轴对称图形,每条边的垂直平
分线是它的对称轴
B.正多边形是中心对称图形,正多边形的中
心是它的对称中心
C.正多边形的每一个外角都等于该正多边形
的中心角
D.正多边形的每一个内角都与该正多边形的
中心角互补
3.如果一个四边形的外接圆与内切圆是同心圆,
那么这个四边形一定是
A.矩形
B.菱形
C.正方形
D.不能确定
4.在半径为R的圆上依次截取长度等于R的
弦,顺次连接各分点得到的多边形是(D
A.正三角形
B.正四边形
C.正五边形
D.正六边形
知识点2正多边形的计算
如果一个正多边形的中心角等于72°,那么这
个正多边形的边数是
B
A.4
D.7
6.若正方形的边长为6,则其内切圆的半径(边
心距)为
B.3
C.6
D.6√2
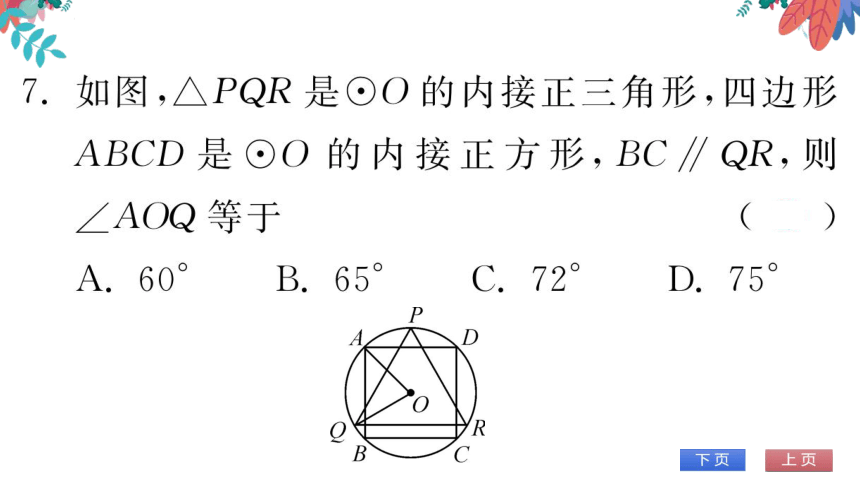
图,△PQR是⊙O的内接正三角形,四边形
ABCD是⊙O的内接正方形,BC∥QR,则
AOQ等于
A.60
D
O
B
(第7题图)
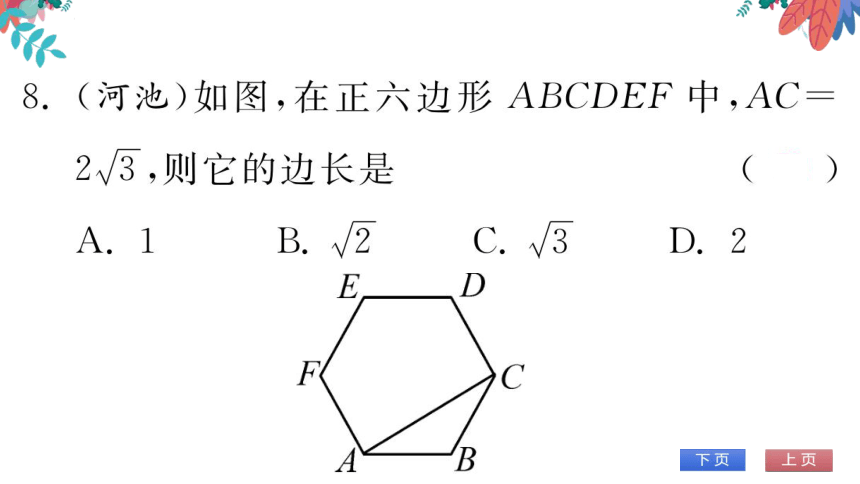
F
少C
(第8题图)
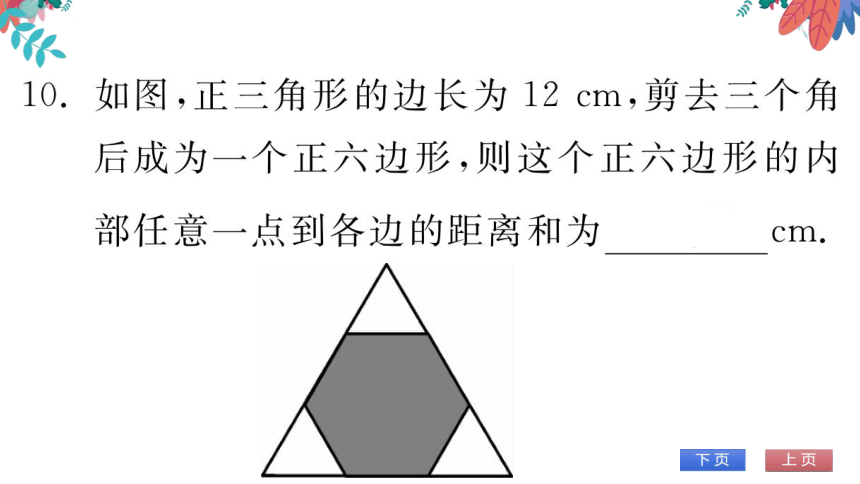
(第10题图)
1.如图,正△ABC的边长为12,求它的边心距、
半径和面积
解:设点O是边长为12的正
△ABC的中心,过点O作
OH⊥BC于点H,连接
OB,则
BH C
1、360°
在Rt△BOH中,∠BOH=
60°
BH
bc=6
OBH=30°
设OH=x,则OB=2x,∴x2+62=(2x)2
.c
OH=23,OB=43
△ABC
6×BH·OH=3×6×2√3=363
答:它的边心距为23,半径为43,面积为
363
规律方法全练
提升能力
12.(德阳)已知圆内接正三角形的面积为√3,则
该圆的内接正六边形的边心距是
A.2
13.(达州)以半径为2的圆的内接正三角形、正
方形、正六边形的边心距为三边作三角形,则
该三角形的面积为
4.如图,正五边形 ABCDE内接于⊙O,过点A
作⊙O的切线交对角线DB的延长线于点
F,则下列结论中不成立的是
A.AE∥BF
B.AF∥CD
C. DE
D. AB=BE
5.(扬州)如图,AC是⊙O的内接正六边形的
边,点B在AC上,且BC是⊙O的内接正十
边形的一边,若AB是⊙O的内接正n边形
的一边,则n=15