北师大版八年级数学上册 7.5 三角形内角和定理(共21张PPT)
文档属性
| 名称 | 北师大版八年级数学上册 7.5 三角形内角和定理(共21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 949.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 06:54:06 | ||
图片预览








文档简介
(共21张PPT)
三角形内角和定理
1.掌握三角形内角和定理的证明及其简单应用.
2.初步掌握利用辅助线证明,体会思维实验和符号化的理性作用.
3.通过一题多解,初步体会思维的多向性,引导学生的个性化发展.
1
A
B
D
2
3
C
如图,我们把∠A移到了∠1的
位置,∠B移到了∠2的位置.就得到
了三角形三个内角的和等于
180°.
根据前面的公理和定理,你能用自己的语言说说这一结论的证明思路吗 你能用比较简捷的语言写出这一证明过程吗 与同伴交流.
已知:如图,△ABC.
求证:∠A+∠B+∠C=180°.
分析:延长BC到D,过点C作射线CE∥AB,这样,就相当于把∠A移到了∠1的位置,把∠B移到了∠2的位置.
A
B
C
证明:作BC的延长线CD,过点C作射线CE∥AB,则
∠1=∠A(两直线平行,内错角相等),
∠2= ∠B(两直线平行,同位角相等).
又∵∠1+∠2+∠3= 180° (平角的定义),
∴∠A+∠B+∠ACB= 180° (等量代换).
你还有其他方法来证明三角形内角和定理吗
这里的CD,CE称为辅助线,辅助线通常画成虚线.
A
B
C
E
2
1
3
D
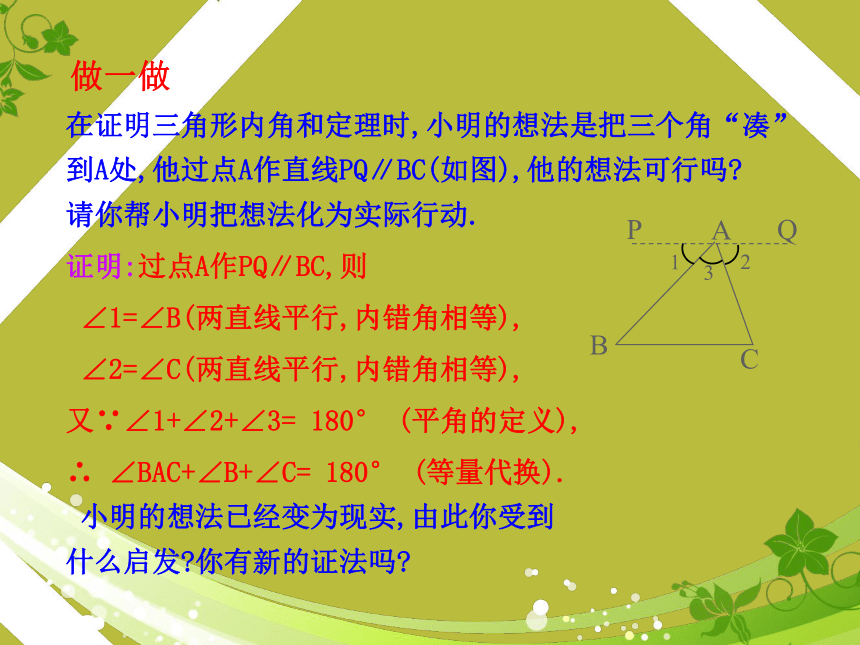
在证明三角形内角和定理时,小明的想法是把三个角“凑”到A处,他过点A作直线PQ∥BC(如图),他的想法可行吗
请你帮小明把想法化为实际行动.
证明:过点A作PQ∥BC,则
∠1=∠B(两直线平行,内错角相等),
∠2=∠C(两直线平行,内错角相等),
又∵∠1+∠2+∠3= 180° (平角的定义),
∴ ∠BAC+∠B+∠C= 180° (等量代换).
小明的想法已经变为现实,由此你受到
什么启发 你有新的证法吗
A
B
C
P
Q
做一做
2
3
1
如图. ∠1是△ABC的一个外角, ∠1与图中的其他角有什么关系
∠1+∠4=180°;
∠1>∠2;
∠1>∠3;
∠1=∠2+∠3.
A
B
C
D
1
2
3
4
证明:∵∠2+∠3+∠4=180° (三角形内角和定理),
∠1+∠4=180° (平角的定义),
∴∠1= ∠2+∠3.(等量代换).
∴ ∠1>∠2,∠1>∠3(和大于部分).
用文字表述为:
三角形的一个外角等于和它不相邻的两个内角的和.
三角形的一个外角大于任何一个和它不相邻的内角.
在这里,我们通过三角形的内角和定理
直接推导出两个新定理.像这样,由一
个基本事实或定理直接推出的定理,
叫做这个基本事实或定理的推论.
推论可以当做定理使用.
三角形内角和定理的推论:
定理: 三角形的一个外角等于和它不相邻的两个内角的和.
定理: 三角形的一个外角大于任何一个和它不相邻的内角.
A
B
C
D
1
2
3
4
A
B
C
D
1
2
3
4
在△ABC中:
∠1=∠2+∠3;
所以∠1>∠2,∠1>∠3.
这个结论以后可以直接运用.
例 已知:如图,在△ABC中,AD平分外角∠EAC,
∠B= ∠C. 求证:AD∥BC.
分析:要证明AD∥BC,只需要证明“同位角相等”
或“内错角相等”或“同旁内角互补”.
证明:∵∠EAC=∠B+∠C (三角形的一个外角等于和它不相邻的两个内角的和),∠B=∠C (已知),
∴∠C= ∠EAC(等式的性质).
∵AD平分 ∠EAC(已知).
∴∠DAC= ∠EAC(角平分线的定义).
∴∠DAC=∠C(等量代换).
∴AD∥BC(内错角相等,两直线平行).
A
C
D
B
E
例题是运用了定理“内错角相等,两直线平行”得到了证实.
【例题】
已知:如图,在△ABC中, ∠1是
它的一个外角, E为边AC上一点,延
长BC到D,连接DE.
求证: ∠1>∠2.
C
A
B
F
1
3
4
5
E
D
2
【做一做】
证明:∵∠1是△ABC的一个外角(已知),
∴∠1>∠3(三角形的一个外角大于任何一个和它不相邻的内角).
∵∠3是△CDE的一个外角 (外角定义).
∴∠3>∠2(三角形的一个外角大于任何一个和它不相邻的内角).
∴∠1>∠2(不等式的性质).
把你所悟到的证明一个真命题的方法,步骤,书写格式以及注意事项转化为一种方法.
C
B
A
如果BC不动,把点A“拉离”BC,
那么当点A越来越远离BC时,∠A就
越来越小(越来越接近0°),而
∠B和∠C则越来越大,它们的和
越来越接近180°, 当把点A拉
到无穷远时,便有AB∥AC,∠B和
∠C成为同旁内角,它们的和等于180°.由此你能想到什么
读一读
C
B
A
在△ABC中,如果BC不动,把点A“压”向BC,那么当点A越来越接近BC时, ∠A就越来越大(越来越接近180°),而∠B和∠C越来越小(越来越接近0°).由此你能想到什么
1.如图所示,
在△ABC中,CD是∠ACB的平分线,
∠A=80°,∠B=60°,
那么∠BDC=( )
A.80° B.90°
C.100° D.110°
2.若一个三角形三个内角度数的比为2∶3∶4,那么这个三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.等边三角形
【解析】选B.由题意可设这个三角形的三个内角度数分别
为2x,3x,4x,根据三角形内角和定理可得:2x+3x+4x=180°,
得x=20°,因此可得三个内角度数分别为40°,60°,80°.
3.如图,D,E分别是AB,AC上的点,若∠A=70°,∠B=60°,DE∥BC,则∠AED的度数是____.
【解析】因为∠A=70°,∠B=60°,所以∠C=50°,
又因为DE//BC,所以∠AED=∠C=50°.
答案:50°
4. 如图,在△ABC中,∠A=60°,
∠B=70°,∠ACB的平分线交AB于D,
DE∥BC交AC于E,求∠EDC和∠BDC的
度数.
【解析】∵∠A=60°,∠B=70°,∴∠ACB=180°-60°
-70°=50°,∵CD是∠ACB的平分线,
∴∠ACD=∠BCD=25°,∵DE∥BC,∴∠EDC=∠BCD=25°.
在△BCD中,∠B=70°,∠BCD=25°,
∴∠BDC=180°-70°-25°=85°.
通过本课时的学习,需要我们掌握:
1.三角形的内角和是180°.
2.证明三角形内角和是180°,不仅可以通过实验操作验证,还可以通过严密的推理得到证明.通过平行线将三个内角拼在一起,得到一个平角或构造同旁内角是常用方法.
3.△ABC中,∠A+∠B+∠C=180°.
推论1: 三角形的一个外角等于和它不相邻的两个内角的和.
推论2: 三角形的一个外角大于任何一个和它不相邻的内角.
要在座的人都停止了说话的时候,有了机会,方才可以谦逊地把问题提出,向人学习。
——约翰 洛克
三角形内角和定理
1.掌握三角形内角和定理的证明及其简单应用.
2.初步掌握利用辅助线证明,体会思维实验和符号化的理性作用.
3.通过一题多解,初步体会思维的多向性,引导学生的个性化发展.
1
A
B
D
2
3
C
如图,我们把∠A移到了∠1的
位置,∠B移到了∠2的位置.就得到
了三角形三个内角的和等于
180°.
根据前面的公理和定理,你能用自己的语言说说这一结论的证明思路吗 你能用比较简捷的语言写出这一证明过程吗 与同伴交流.
已知:如图,△ABC.
求证:∠A+∠B+∠C=180°.
分析:延长BC到D,过点C作射线CE∥AB,这样,就相当于把∠A移到了∠1的位置,把∠B移到了∠2的位置.
A
B
C
证明:作BC的延长线CD,过点C作射线CE∥AB,则
∠1=∠A(两直线平行,内错角相等),
∠2= ∠B(两直线平行,同位角相等).
又∵∠1+∠2+∠3= 180° (平角的定义),
∴∠A+∠B+∠ACB= 180° (等量代换).
你还有其他方法来证明三角形内角和定理吗
这里的CD,CE称为辅助线,辅助线通常画成虚线.
A
B
C
E
2
1
3
D
在证明三角形内角和定理时,小明的想法是把三个角“凑”到A处,他过点A作直线PQ∥BC(如图),他的想法可行吗
请你帮小明把想法化为实际行动.
证明:过点A作PQ∥BC,则
∠1=∠B(两直线平行,内错角相等),
∠2=∠C(两直线平行,内错角相等),
又∵∠1+∠2+∠3= 180° (平角的定义),
∴ ∠BAC+∠B+∠C= 180° (等量代换).
小明的想法已经变为现实,由此你受到
什么启发 你有新的证法吗
A
B
C
P
Q
做一做
2
3
1
如图. ∠1是△ABC的一个外角, ∠1与图中的其他角有什么关系
∠1+∠4=180°;
∠1>∠2;
∠1>∠3;
∠1=∠2+∠3.
A
B
C
D
1
2
3
4
证明:∵∠2+∠3+∠4=180° (三角形内角和定理),
∠1+∠4=180° (平角的定义),
∴∠1= ∠2+∠3.(等量代换).
∴ ∠1>∠2,∠1>∠3(和大于部分).
用文字表述为:
三角形的一个外角等于和它不相邻的两个内角的和.
三角形的一个外角大于任何一个和它不相邻的内角.
在这里,我们通过三角形的内角和定理
直接推导出两个新定理.像这样,由一
个基本事实或定理直接推出的定理,
叫做这个基本事实或定理的推论.
推论可以当做定理使用.
三角形内角和定理的推论:
定理: 三角形的一个外角等于和它不相邻的两个内角的和.
定理: 三角形的一个外角大于任何一个和它不相邻的内角.
A
B
C
D
1
2
3
4
A
B
C
D
1
2
3
4
在△ABC中:
∠1=∠2+∠3;
所以∠1>∠2,∠1>∠3.
这个结论以后可以直接运用.
例 已知:如图,在△ABC中,AD平分外角∠EAC,
∠B= ∠C. 求证:AD∥BC.
分析:要证明AD∥BC,只需要证明“同位角相等”
或“内错角相等”或“同旁内角互补”.
证明:∵∠EAC=∠B+∠C (三角形的一个外角等于和它不相邻的两个内角的和),∠B=∠C (已知),
∴∠C= ∠EAC(等式的性质).
∵AD平分 ∠EAC(已知).
∴∠DAC= ∠EAC(角平分线的定义).
∴∠DAC=∠C(等量代换).
∴AD∥BC(内错角相等,两直线平行).
A
C
D
B
E
例题是运用了定理“内错角相等,两直线平行”得到了证实.
【例题】
已知:如图,在△ABC中, ∠1是
它的一个外角, E为边AC上一点,延
长BC到D,连接DE.
求证: ∠1>∠2.
C
A
B
F
1
3
4
5
E
D
2
【做一做】
证明:∵∠1是△ABC的一个外角(已知),
∴∠1>∠3(三角形的一个外角大于任何一个和它不相邻的内角).
∵∠3是△CDE的一个外角 (外角定义).
∴∠3>∠2(三角形的一个外角大于任何一个和它不相邻的内角).
∴∠1>∠2(不等式的性质).
把你所悟到的证明一个真命题的方法,步骤,书写格式以及注意事项转化为一种方法.
C
B
A
如果BC不动,把点A“拉离”BC,
那么当点A越来越远离BC时,∠A就
越来越小(越来越接近0°),而
∠B和∠C则越来越大,它们的和
越来越接近180°, 当把点A拉
到无穷远时,便有AB∥AC,∠B和
∠C成为同旁内角,它们的和等于180°.由此你能想到什么
读一读
C
B
A
在△ABC中,如果BC不动,把点A“压”向BC,那么当点A越来越接近BC时, ∠A就越来越大(越来越接近180°),而∠B和∠C越来越小(越来越接近0°).由此你能想到什么
1.如图所示,
在△ABC中,CD是∠ACB的平分线,
∠A=80°,∠B=60°,
那么∠BDC=( )
A.80° B.90°
C.100° D.110°
2.若一个三角形三个内角度数的比为2∶3∶4,那么这个三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.等边三角形
【解析】选B.由题意可设这个三角形的三个内角度数分别
为2x,3x,4x,根据三角形内角和定理可得:2x+3x+4x=180°,
得x=20°,因此可得三个内角度数分别为40°,60°,80°.
3.如图,D,E分别是AB,AC上的点,若∠A=70°,∠B=60°,DE∥BC,则∠AED的度数是____.
【解析】因为∠A=70°,∠B=60°,所以∠C=50°,
又因为DE//BC,所以∠AED=∠C=50°.
答案:50°
4. 如图,在△ABC中,∠A=60°,
∠B=70°,∠ACB的平分线交AB于D,
DE∥BC交AC于E,求∠EDC和∠BDC的
度数.
【解析】∵∠A=60°,∠B=70°,∴∠ACB=180°-60°
-70°=50°,∵CD是∠ACB的平分线,
∴∠ACD=∠BCD=25°,∵DE∥BC,∴∠EDC=∠BCD=25°.
在△BCD中,∠B=70°,∠BCD=25°,
∴∠BDC=180°-70°-25°=85°.
通过本课时的学习,需要我们掌握:
1.三角形的内角和是180°.
2.证明三角形内角和是180°,不仅可以通过实验操作验证,还可以通过严密的推理得到证明.通过平行线将三个内角拼在一起,得到一个平角或构造同旁内角是常用方法.
3.△ABC中,∠A+∠B+∠C=180°.
推论1: 三角形的一个外角等于和它不相邻的两个内角的和.
推论2: 三角形的一个外角大于任何一个和它不相邻的内角.
要在座的人都停止了说话的时候,有了机会,方才可以谦逊地把问题提出,向人学习。
——约翰 洛克
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
