北师大版八年级数学上册 7.5三角形外角定理的证明(1)(共18张PPT)
文档属性
| 名称 | 北师大版八年级数学上册 7.5三角形外角定理的证明(1)(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 06:58:44 | ||
图片预览

文档简介
(共18张PPT)
7.5.2 三角形内角和定理(2)
——三角形的外角
北师大版初中数学八年级上册
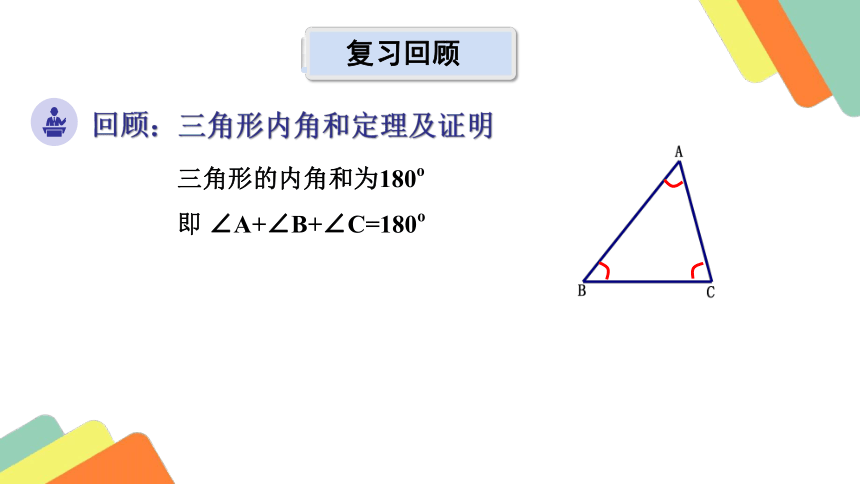
回顾:三角形内角和定理及证明
复习回顾
三角形的内角和为180o
即 ∠A+∠B+∠C=180o
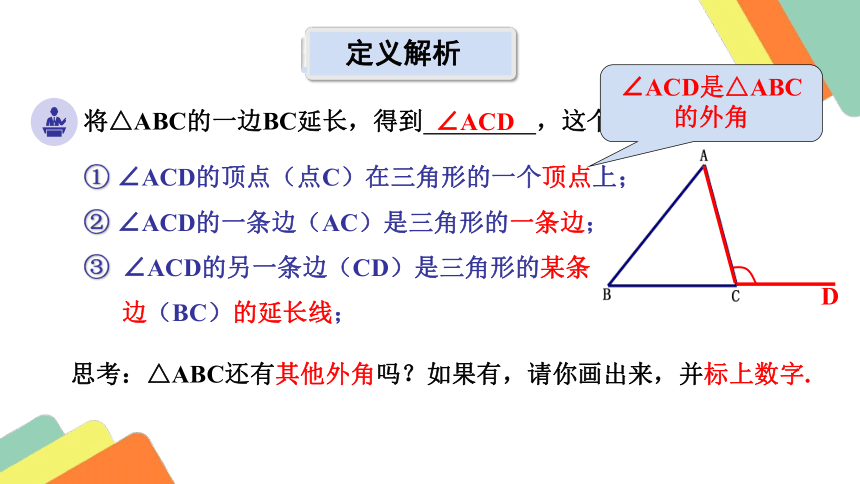
将△ABC的一边BC延长,得到 ,这个角有何特征?
① ∠ACD的顶点(点C)在三角形的一个顶点上;
② ∠ACD的一条边(AC)是三角形的一条边;
③ ∠ACD的另一条边(CD)是三角形的某条
边(BC)的延长线;
定义解析
思考:△ABC还有其他外角吗?如果有,请你画出来,并标上数字.
∠ACD
∠ACD是△ABC的外角
D
1
2
3
4
5
6
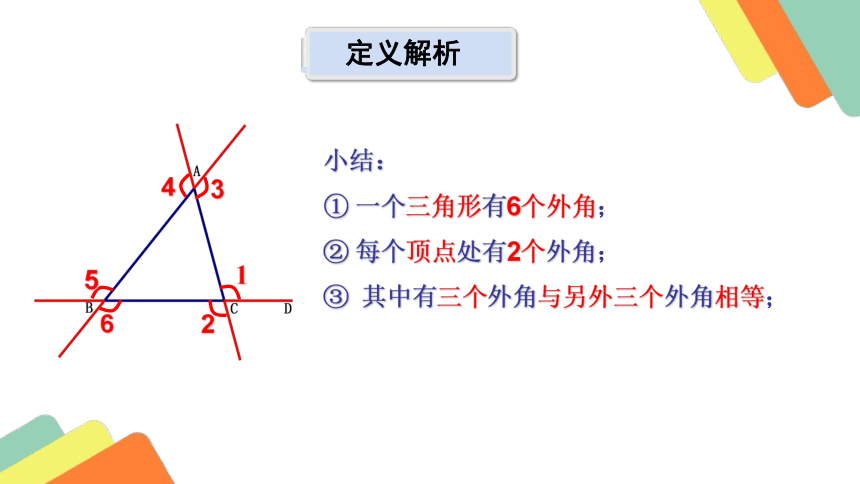
小结:
① 一个三角形有6个外角;
② 每个顶点处有2个外角;
③ 其中有三个外角与另外三个外角相等;
定义解析
2
1
3
4
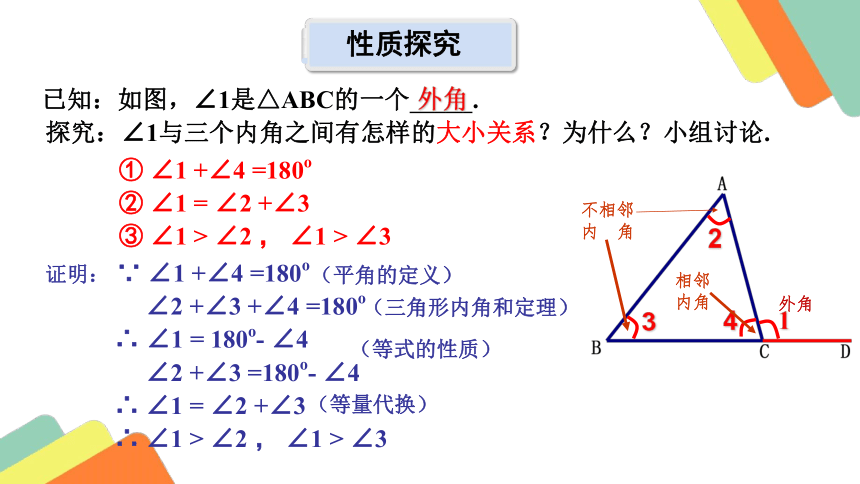
性质探究
外角
相邻内角
不相邻 内 角
已知:如图,∠1是△ABC的一个 .
探究:∠1与三个内角之间有怎样的大小关系?为什么?小组讨论.
外角
① ∠1 +∠4 =180o
② ∠1 = ∠2 +∠3
③ ∠1 > ∠2 , ∠1 > ∠3
证明: ∵ ∠1 +∠4 =180o
∠2 +∠3 +∠4 =180o
∴ ∠1 = 180o- ∠4
∠2 +∠3 =180o- ∠4
∴ ∠1 = ∠2 +∠3
∴ ∠1 > ∠2 , ∠1 > ∠3
(三角形内角和定理)
(平角的定义)
(等式的性质)
(等量代换)
4
2
1
3
① ∠1 +∠4 =180o
② ∠1 = ∠2 +∠3
③ ∠1 > ∠2 , ∠1 > ∠3
1
3
4
2
3
4
2
1
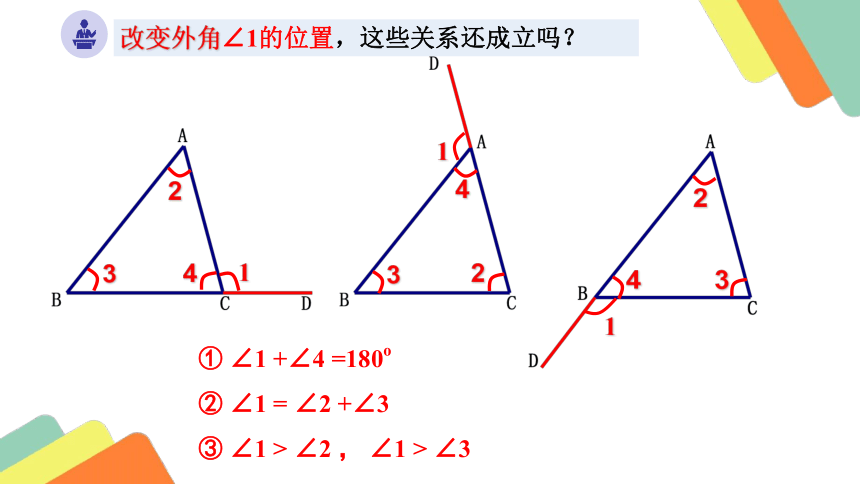
改变外角∠1的位置,这些关系还成立吗?
4
2
1
3
① ∠1 +∠4 =180o
② ∠1 = ∠2 +∠3
③ ∠1 > ∠2 , ∠1 > ∠3
1
3
4
2
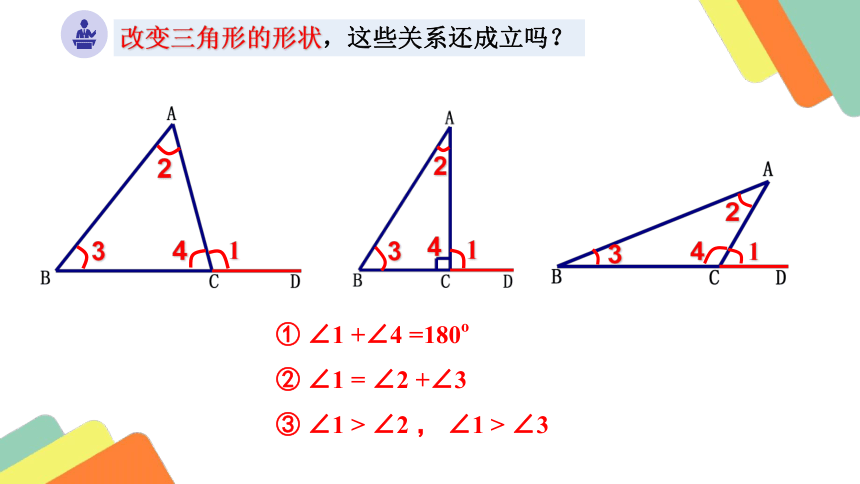
改变三角形的形状,这些关系还成立吗?
1
2
4
3
性质归纳
2
1
3
4
不相邻 内 角
外角
相邻内角
① ∠1 +∠4 =180o
② ∠1 = ∠2 +∠3
③ ∠1 > ∠2 , ∠1 > ∠3
你能用文字语言归纳这些性质吗?
定理1:三角形的一个外角等于和它不相邻的两个内角的和.
性质归纳
定理2:三角形的一个外角大于任何一个和它不相邻的内角.
三角形内角和定理的两条“推论”
判断角的不等关系
由公理、定理直接推出的定理叫做推论。
三角形的内角
三角形的外角
转化
A
C
B
1
80O
60O
100O
1
45O
80O
140O
1
A
B
A
B
C
C
知识应用
1. 求出下列图形中∠1的度数.
∠1= ;
∠1= ;
∠1= ;
140o
55o
120o
知识应用
2. 如图,在△ABC中, ∠1是它的一个外角, E为边AC上一点,延长BC到D,
连接DE,则∠1 ∠D.(填“>,<,=”)
证明:∵ ∠1是△ABC的一个外角
∴ ∠1>∠2
又 ∵ ∠2是△CDE的一个外角
∴ ∠2>∠D
∴ ∠1>∠D
1
>
2
方法巩固
例1 已知: 如图,在△ABC中,∠B=∠C ,AD平分∠EAC.
(1)找出图中△ABC的外角;
(2)求证:AD∥ BC
思考: 如何证明两条直线平行?
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
(∠EAC)
√
还有其他
方法吗?
方法巩固
例1 已知: 如图,在△ABC中,∠B=∠C ,AD平分∠EAC.
(1)找出图中△ABC的外角;
(2)求证:AD∥ BC
思考: 如何证明两条直线平行?
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
(∠EAC)
√
√
合作提升
例2 已知:如图,P是△ABC内一点,连接PB,PC.
求证:∠BPC >∠A.
思考:
①我们有哪些关于角的不等关系的结论?
②本题能直接运用这个结论吗?
③困难在哪里?
④如何构造三角形的外角?
你能想出
几种方法?
(三角形的一个外角大于任何一个和它不相邻的内角)
合作提升
例2 已知:如图,P是△ABC内一点,连接PB,PC.
求证:∠BPC >∠A.
(三角形的一个外角大于任何一个和它不相邻的内角)
添加辅助线
构造三角形(外角)
问1:本节课学习了什么知识?
问2:三角形外角的两条性质定理有什么作用?
问3:如果图中没有三角形或三角形的外角怎么办?
反思感悟
三角形的内角
三角形的外角
转化
判断角的不等关系
添加辅助线
必做题:课本P183 习题7.7:1-4
选做题:补充练习1、2
课后作业
谢谢!再见!
7.5.2 三角形内角和定理(2)
——三角形的外角
北师大版初中数学八年级上册
回顾:三角形内角和定理及证明
复习回顾
三角形的内角和为180o
即 ∠A+∠B+∠C=180o
将△ABC的一边BC延长,得到 ,这个角有何特征?
① ∠ACD的顶点(点C)在三角形的一个顶点上;
② ∠ACD的一条边(AC)是三角形的一条边;
③ ∠ACD的另一条边(CD)是三角形的某条
边(BC)的延长线;
定义解析
思考:△ABC还有其他外角吗?如果有,请你画出来,并标上数字.
∠ACD
∠ACD是△ABC的外角
D
1
2
3
4
5
6
小结:
① 一个三角形有6个外角;
② 每个顶点处有2个外角;
③ 其中有三个外角与另外三个外角相等;
定义解析
2
1
3
4
性质探究
外角
相邻内角
不相邻 内 角
已知:如图,∠1是△ABC的一个 .
探究:∠1与三个内角之间有怎样的大小关系?为什么?小组讨论.
外角
① ∠1 +∠4 =180o
② ∠1 = ∠2 +∠3
③ ∠1 > ∠2 , ∠1 > ∠3
证明: ∵ ∠1 +∠4 =180o
∠2 +∠3 +∠4 =180o
∴ ∠1 = 180o- ∠4
∠2 +∠3 =180o- ∠4
∴ ∠1 = ∠2 +∠3
∴ ∠1 > ∠2 , ∠1 > ∠3
(三角形内角和定理)
(平角的定义)
(等式的性质)
(等量代换)
4
2
1
3
① ∠1 +∠4 =180o
② ∠1 = ∠2 +∠3
③ ∠1 > ∠2 , ∠1 > ∠3
1
3
4
2
3
4
2
1
改变外角∠1的位置,这些关系还成立吗?
4
2
1
3
① ∠1 +∠4 =180o
② ∠1 = ∠2 +∠3
③ ∠1 > ∠2 , ∠1 > ∠3
1
3
4
2
改变三角形的形状,这些关系还成立吗?
1
2
4
3
性质归纳
2
1
3
4
不相邻 内 角
外角
相邻内角
① ∠1 +∠4 =180o
② ∠1 = ∠2 +∠3
③ ∠1 > ∠2 , ∠1 > ∠3
你能用文字语言归纳这些性质吗?
定理1:三角形的一个外角等于和它不相邻的两个内角的和.
性质归纳
定理2:三角形的一个外角大于任何一个和它不相邻的内角.
三角形内角和定理的两条“推论”
判断角的不等关系
由公理、定理直接推出的定理叫做推论。
三角形的内角
三角形的外角
转化
A
C
B
1
80O
60O
100O
1
45O
80O
140O
1
A
B
A
B
C
C
知识应用
1. 求出下列图形中∠1的度数.
∠1= ;
∠1= ;
∠1= ;
140o
55o
120o
知识应用
2. 如图,在△ABC中, ∠1是它的一个外角, E为边AC上一点,延长BC到D,
连接DE,则∠1 ∠D.(填“>,<,=”)
证明:∵ ∠1是△ABC的一个外角
∴ ∠1>∠2
又 ∵ ∠2是△CDE的一个外角
∴ ∠2>∠D
∴ ∠1>∠D
1
>
2
方法巩固
例1 已知: 如图,在△ABC中,∠B=∠C ,AD平分∠EAC.
(1)找出图中△ABC的外角;
(2)求证:AD∥ BC
思考: 如何证明两条直线平行?
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
(∠EAC)
√
还有其他
方法吗?
方法巩固
例1 已知: 如图,在△ABC中,∠B=∠C ,AD平分∠EAC.
(1)找出图中△ABC的外角;
(2)求证:AD∥ BC
思考: 如何证明两条直线平行?
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
(∠EAC)
√
√
合作提升
例2 已知:如图,P是△ABC内一点,连接PB,PC.
求证:∠BPC >∠A.
思考:
①我们有哪些关于角的不等关系的结论?
②本题能直接运用这个结论吗?
③困难在哪里?
④如何构造三角形的外角?
你能想出
几种方法?
(三角形的一个外角大于任何一个和它不相邻的内角)
合作提升
例2 已知:如图,P是△ABC内一点,连接PB,PC.
求证:∠BPC >∠A.
(三角形的一个外角大于任何一个和它不相邻的内角)
添加辅助线
构造三角形(外角)
问1:本节课学习了什么知识?
问2:三角形外角的两条性质定理有什么作用?
问3:如果图中没有三角形或三角形的外角怎么办?
反思感悟
三角形的内角
三角形的外角
转化
判断角的不等关系
添加辅助线
必做题:课本P183 习题7.7:1-4
选做题:补充练习1、2
课后作业
谢谢!再见!
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
