北师大版八年级数学上册 第四章 一次函数4.4 一次函数的应用(共21张PPT)
文档属性
| 名称 | 北师大版八年级数学上册 第四章 一次函数4.4 一次函数的应用(共21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 07:03:08 | ||
图片预览




文档简介
(共21张PPT)
一次函数图象的应用
复习旧知
图象分析方法:
(1)从函数图象的形状判断函数类型;
(2)从x轴、y轴的实际意义去理解图象上点的坐标
的实际意义。
诊断练习
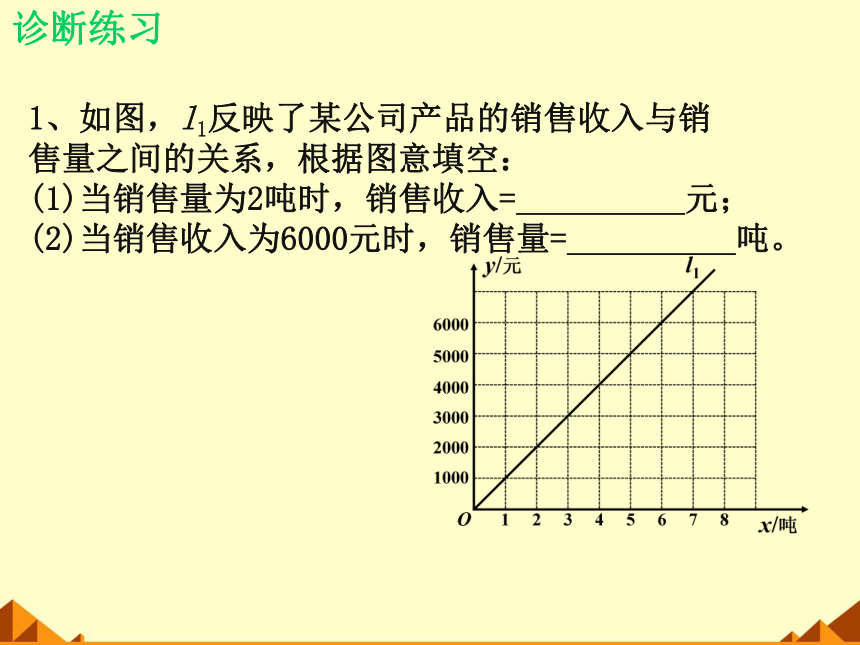
1、如图,l1反映了某公司产品的销售收入与销
售量之间的关系,根据图意填空:
(1)当销售量为2吨时,销售收入= 元;
(2)当销售收入为6000元时,销售量= 吨。
诊断练习
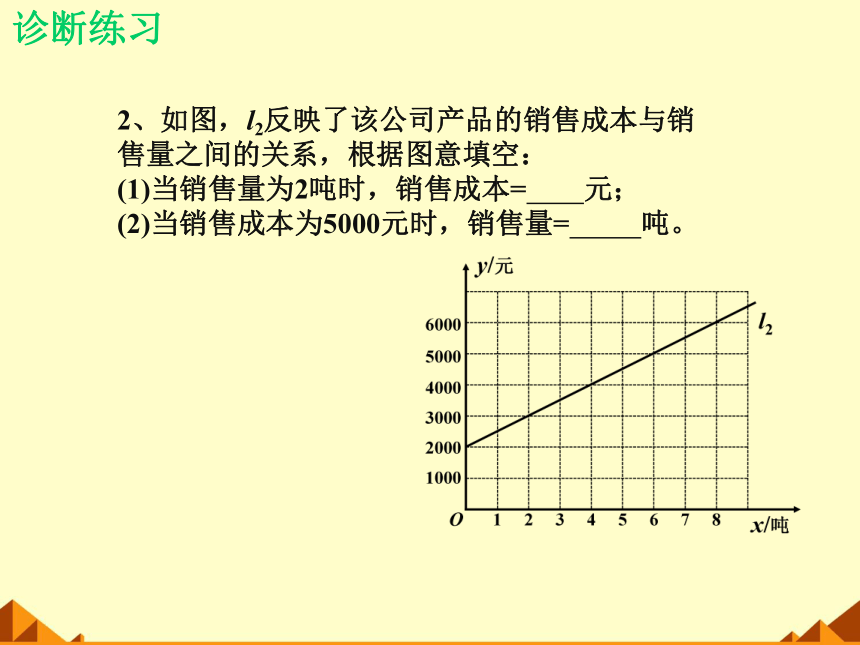
2、如图,l2反映了该公司产品的销售成本与销
售量之间的关系,根据图意填空:
(1)当销售量为2吨时,销售成本= 元;
(2)当销售成本为5000元时,销售量= 吨。
情景引入
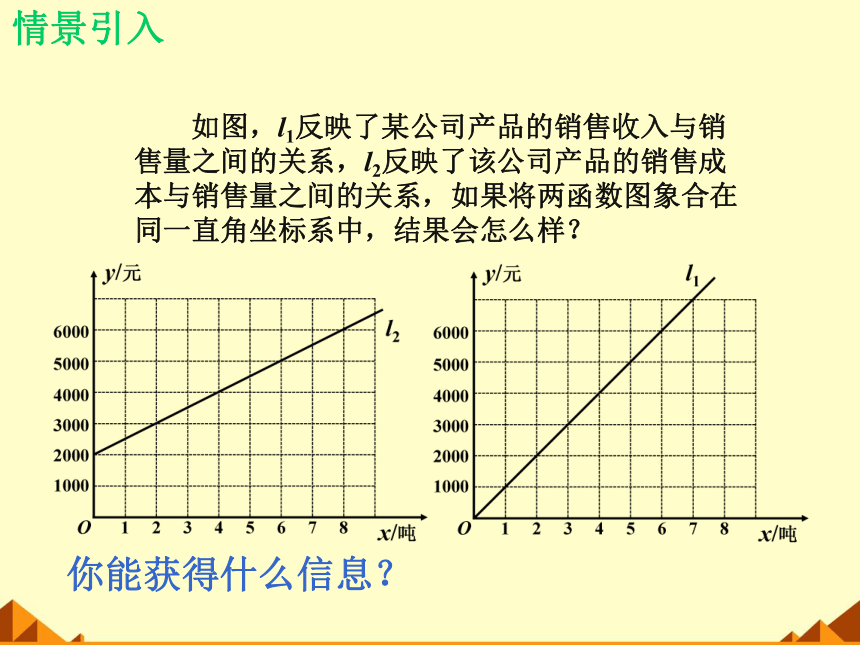
如图,l1反映了某公司产品的销售收入与销
售量之间的关系,l2反映了该公司产品的销售成
本与销售量之间的关系,如果将两函数图象合在
同一直角坐标系中,结果会怎么样?
你能获得什么信息?
二、学习目标
1、进一步训练学生的识图能力,能利用函数图象解决简单的实际问题。
2、通过函数图象获取信息,进一步培养学生的数形结合意识。
际问题。
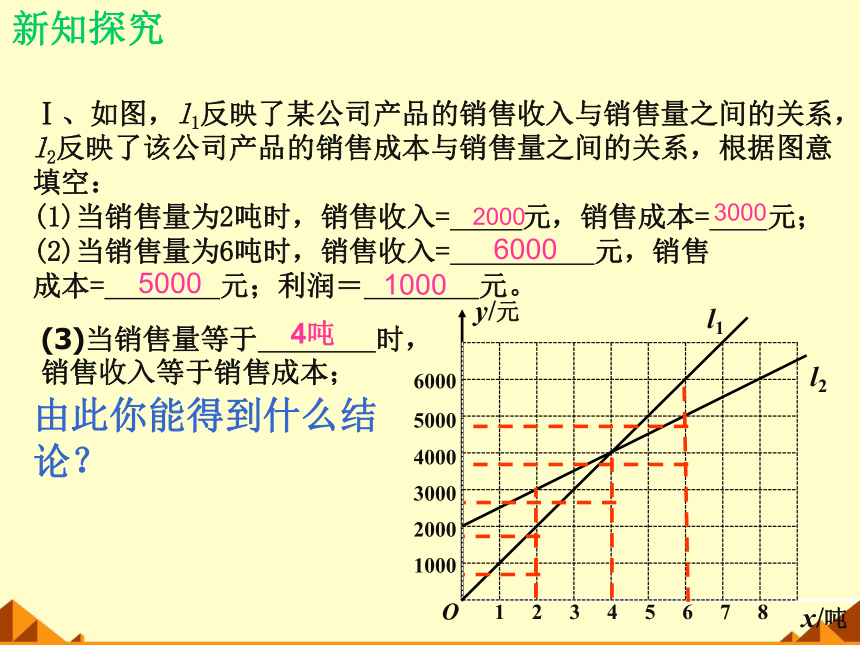
Ⅰ、如图,l1反映了某公司产品的销售收入与销售量之间的关系,l2反映了该公司产品的销售成本与销售量之间的关系,根据图意填空:
(1)当销售量为2吨时,销售收入= 元,销售成本= 元; (2)当销售量为6吨时,销售收入= 元,销售
成本= 元;利润= 元。
1 2 3 4 5 6 7 8
y/元
O
6000
5000
4000
3000
2000
1000
x/吨
l2
l1
新知探究
2000
3000
6000
5000
1000
(3)当销售量等于 时,销售收入等于销售成本;
4吨
由此你能得到什么结论?
新知归纳
两直线交点的意义:
(1)几何意义:两直线交点是它们的公共点;
(2)代数意义:两直线交点的坐标同时满足两个
解析式。
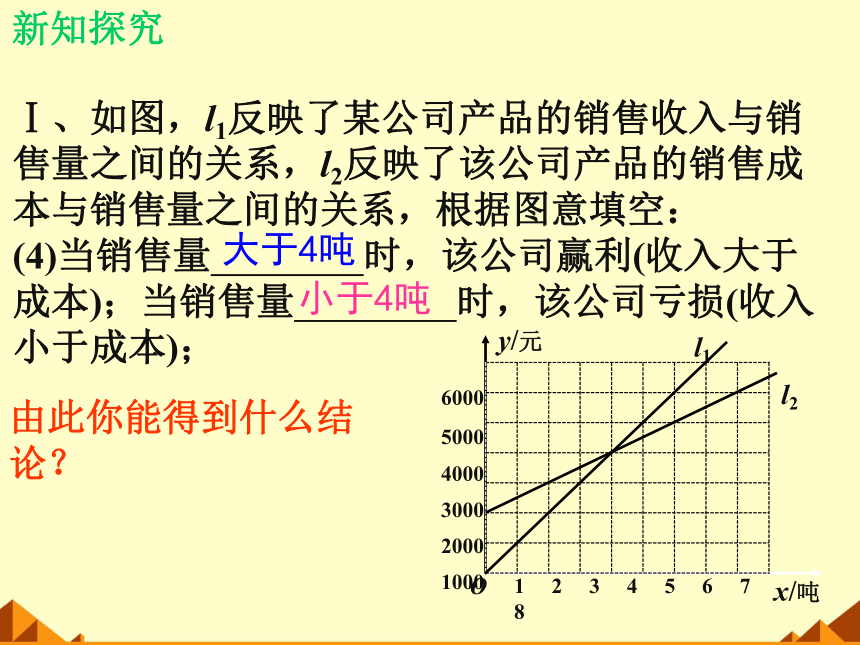
Ⅰ、如图,l1反映了某公司产品的销售收入与销
售量之间的关系,l2反映了该公司产品的销售成
本与销售量之间的关系,根据图意填空:
(4)当销售量 时,该公司赢利(收入大于
成本);当销售量 时,该公司亏损(收入
小于成本);
新知探究
由此你能得到什么结论?
1 2 3 4 5 6 7 8
y/元
O
6000
5000
4000
3000
2000
1000
x/吨
l2
l1
大于4吨
小于4吨
新知归纳
利用图象比较函数值的方法:
(1)先找交点坐标,交点处y1=y2;
(2)再看交点左右两侧,图象位于上方的直线函
数值较大。
Ⅰ、如图,l1反映了某公司产品的销售收入与销
售量之间的关系,l2反映了该公司产品的销售成
本与销售量之间的关系,根据图意填空:
(5) l1对应的函数表达式是 ,
l2对应的函数表达式是 。
新知探究
y=1000x
1 2 3 4 5 6 7 8
y/元
O
6000
5000
4000
3000
2000
1000
x/吨
l2
l1
y=500x+2000
1、如图,l1反映了某公司产品的销售收入与销
售量之间的关系,l2反映了该公司产品的销售成
本与销售量之间的关系,根据图意填空:
x=3时,销售收入= ,销售成本= ,
赢利(收入 成本)= 。
巩固练习
1 2 3 4 5 6 7 8
y/元
O
6000
5000
4000
3000
2000
1000
x/吨
l2
l1
例1、我边防局接到情报,近海处有一可疑船只A正向公海方向行驶,边防局迅速派出快艇B追赶,图中l1、l2分别表示两船相对于海岸的距离s(海里)与追赶时间t(分)之间的关系。
根据图象回答下列问题:
范例讲解
海
岸
公
海
B
A
(1)哪条线表示B到海岸的距离与追赶时间之间的关系?
解:观察图象,得 当t=0时,
B距海岸0海里,即
S=0,
故 l1 表示 B 到海岸的距离与追赶时间之间的关系;
海
岸
公
海
A
B
2
4
6
8
10
O
2
4
6
8
t /分
s /海里
l1
l2
B
A
(2)A、B 哪个速度快?
t从0增加到10时,
l2的纵坐标增加了2,
l1的纵坐标增加了5,
海
岸
公
海
A
B
2
4
6
8
10
O
2
4
6
8
t /分
s /海里
l1
l2
B
A
即10分内,
A 行驶了2海里,
B 行驶了5海里,
所以 B 的速度快。
7
5
可以看出,当t=15时,l1上对应点在l2上对应点的下方。
这表明,15分钟时 B尚未追上 A。
海
岸
公
海
A
B
2
4
6
8
10
O
2
4
6
8
t /分
s /海里
l1
l2
B
A
12
14
(3)15分钟内 B
能否追上 A?
15
海
岸
公
海
A
B
2
4
6
8
10
O
2
4
6
8
t /分
s /海里
l1
l2
B
A
12
14
(4)如果一直追下去,那么 B 能否追上 A?
如图延伸l1 、l2 相交于点P。
因此,如果一直追下去,那么 B 一定能追
上 A。
P
海
岸
公
海
A
B
2
4
6
8
10
O
2
4
6
8
t /分
s /海里
l1
l2
B
A
12
14
P
从图中可以看出,l1 与 l2 交点P的纵坐标小于12,
这说明在
A 逃入公海前,我边防快艇 B能够追上 A。
10
(5)当 A 逃到离海岸12海里的公海时,B 将无法对其进行检查。照此速度, B 能否在 A 逃入公海前将其拦截?
1、如图表示甲骑自行车、乙骑摩托车沿相同路线
由A到B地行驶过程中路程与时间的函数图象,两
地相距80千米。
(1)谁出发较早?早多长时间?谁较早到达B地?
早多长时间?
(2)两人在途中的速度分别是
多少?
(3)指出在什么时段内两人均
行驶在途中(不包括两端点)?
甲行驶在乙前面;甲与乙相
遇;甲行驶在乙后面。
甲
乙
【达标检测】
2、小聪和小慧去某风景区游览,约好在“飞瀑”见面,上午7:00小聪乘电动汽车从“古刹”出发,沿景区公路去“飞瀑”,车速为36km/h,小慧也于上午7:00从“塔林”出发,骑电动自行车沿景区公路去“飞瀑”,车速为26km/h.
(1)当小聪追上小慧时,他们是否已经过了“草甸”?
(2)当小聪到达“飞瀑”时,小慧离“飞瀑”还有多少km?
课堂小结
1、两直线交点的意义:
(1)几何意义:两直线交点是它们的公共点;
(2)代数意义:两直线交点的坐标同时满足两个
解析式。
2、利用图象比较函数值的方法:
(1)先找交点坐标,交点处y1=y2;
(2)再看交点左右两侧,图象位于上方的直线函
数值较大。
一次函数图象的应用
复习旧知
图象分析方法:
(1)从函数图象的形状判断函数类型;
(2)从x轴、y轴的实际意义去理解图象上点的坐标
的实际意义。
诊断练习
1、如图,l1反映了某公司产品的销售收入与销
售量之间的关系,根据图意填空:
(1)当销售量为2吨时,销售收入= 元;
(2)当销售收入为6000元时,销售量= 吨。
诊断练习
2、如图,l2反映了该公司产品的销售成本与销
售量之间的关系,根据图意填空:
(1)当销售量为2吨时,销售成本= 元;
(2)当销售成本为5000元时,销售量= 吨。
情景引入
如图,l1反映了某公司产品的销售收入与销
售量之间的关系,l2反映了该公司产品的销售成
本与销售量之间的关系,如果将两函数图象合在
同一直角坐标系中,结果会怎么样?
你能获得什么信息?
二、学习目标
1、进一步训练学生的识图能力,能利用函数图象解决简单的实际问题。
2、通过函数图象获取信息,进一步培养学生的数形结合意识。
际问题。
Ⅰ、如图,l1反映了某公司产品的销售收入与销售量之间的关系,l2反映了该公司产品的销售成本与销售量之间的关系,根据图意填空:
(1)当销售量为2吨时,销售收入= 元,销售成本= 元; (2)当销售量为6吨时,销售收入= 元,销售
成本= 元;利润= 元。
1 2 3 4 5 6 7 8
y/元
O
6000
5000
4000
3000
2000
1000
x/吨
l2
l1
新知探究
2000
3000
6000
5000
1000
(3)当销售量等于 时,销售收入等于销售成本;
4吨
由此你能得到什么结论?
新知归纳
两直线交点的意义:
(1)几何意义:两直线交点是它们的公共点;
(2)代数意义:两直线交点的坐标同时满足两个
解析式。
Ⅰ、如图,l1反映了某公司产品的销售收入与销
售量之间的关系,l2反映了该公司产品的销售成
本与销售量之间的关系,根据图意填空:
(4)当销售量 时,该公司赢利(收入大于
成本);当销售量 时,该公司亏损(收入
小于成本);
新知探究
由此你能得到什么结论?
1 2 3 4 5 6 7 8
y/元
O
6000
5000
4000
3000
2000
1000
x/吨
l2
l1
大于4吨
小于4吨
新知归纳
利用图象比较函数值的方法:
(1)先找交点坐标,交点处y1=y2;
(2)再看交点左右两侧,图象位于上方的直线函
数值较大。
Ⅰ、如图,l1反映了某公司产品的销售收入与销
售量之间的关系,l2反映了该公司产品的销售成
本与销售量之间的关系,根据图意填空:
(5) l1对应的函数表达式是 ,
l2对应的函数表达式是 。
新知探究
y=1000x
1 2 3 4 5 6 7 8
y/元
O
6000
5000
4000
3000
2000
1000
x/吨
l2
l1
y=500x+2000
1、如图,l1反映了某公司产品的销售收入与销
售量之间的关系,l2反映了该公司产品的销售成
本与销售量之间的关系,根据图意填空:
x=3时,销售收入= ,销售成本= ,
赢利(收入 成本)= 。
巩固练习
1 2 3 4 5 6 7 8
y/元
O
6000
5000
4000
3000
2000
1000
x/吨
l2
l1
例1、我边防局接到情报,近海处有一可疑船只A正向公海方向行驶,边防局迅速派出快艇B追赶,图中l1、l2分别表示两船相对于海岸的距离s(海里)与追赶时间t(分)之间的关系。
根据图象回答下列问题:
范例讲解
海
岸
公
海
B
A
(1)哪条线表示B到海岸的距离与追赶时间之间的关系?
解:观察图象,得 当t=0时,
B距海岸0海里,即
S=0,
故 l1 表示 B 到海岸的距离与追赶时间之间的关系;
海
岸
公
海
A
B
2
4
6
8
10
O
2
4
6
8
t /分
s /海里
l1
l2
B
A
(2)A、B 哪个速度快?
t从0增加到10时,
l2的纵坐标增加了2,
l1的纵坐标增加了5,
海
岸
公
海
A
B
2
4
6
8
10
O
2
4
6
8
t /分
s /海里
l1
l2
B
A
即10分内,
A 行驶了2海里,
B 行驶了5海里,
所以 B 的速度快。
7
5
可以看出,当t=15时,l1上对应点在l2上对应点的下方。
这表明,15分钟时 B尚未追上 A。
海
岸
公
海
A
B
2
4
6
8
10
O
2
4
6
8
t /分
s /海里
l1
l2
B
A
12
14
(3)15分钟内 B
能否追上 A?
15
海
岸
公
海
A
B
2
4
6
8
10
O
2
4
6
8
t /分
s /海里
l1
l2
B
A
12
14
(4)如果一直追下去,那么 B 能否追上 A?
如图延伸l1 、l2 相交于点P。
因此,如果一直追下去,那么 B 一定能追
上 A。
P
海
岸
公
海
A
B
2
4
6
8
10
O
2
4
6
8
t /分
s /海里
l1
l2
B
A
12
14
P
从图中可以看出,l1 与 l2 交点P的纵坐标小于12,
这说明在
A 逃入公海前,我边防快艇 B能够追上 A。
10
(5)当 A 逃到离海岸12海里的公海时,B 将无法对其进行检查。照此速度, B 能否在 A 逃入公海前将其拦截?
1、如图表示甲骑自行车、乙骑摩托车沿相同路线
由A到B地行驶过程中路程与时间的函数图象,两
地相距80千米。
(1)谁出发较早?早多长时间?谁较早到达B地?
早多长时间?
(2)两人在途中的速度分别是
多少?
(3)指出在什么时段内两人均
行驶在途中(不包括两端点)?
甲行驶在乙前面;甲与乙相
遇;甲行驶在乙后面。
甲
乙
【达标检测】
2、小聪和小慧去某风景区游览,约好在“飞瀑”见面,上午7:00小聪乘电动汽车从“古刹”出发,沿景区公路去“飞瀑”,车速为36km/h,小慧也于上午7:00从“塔林”出发,骑电动自行车沿景区公路去“飞瀑”,车速为26km/h.
(1)当小聪追上小慧时,他们是否已经过了“草甸”?
(2)当小聪到达“飞瀑”时,小慧离“飞瀑”还有多少km?
课堂小结
1、两直线交点的意义:
(1)几何意义:两直线交点是它们的公共点;
(2)代数意义:两直线交点的坐标同时满足两个
解析式。
2、利用图象比较函数值的方法:
(1)先找交点坐标,交点处y1=y2;
(2)再看交点左右两侧,图象位于上方的直线函
数值较大。
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
