北师大版八年级数学上册 3.3 轴对称与坐标变化2课件(16张)
文档属性
| 名称 | 北师大版八年级数学上册 3.3 轴对称与坐标变化2课件(16张) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 08:56:45 | ||
图片预览

文档简介
(共16张PPT)
变化中的鱼
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
9
10
5
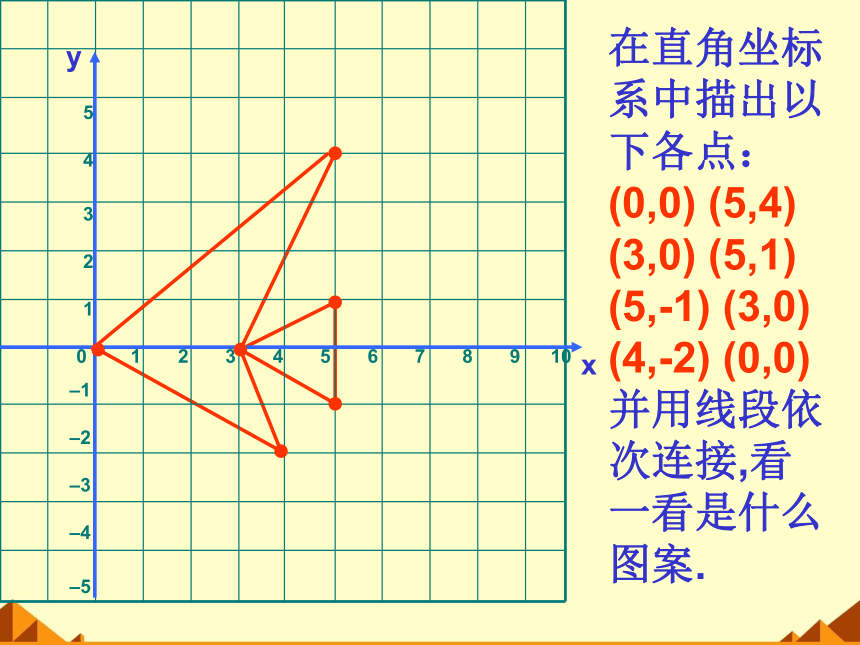
在直角坐标系中描出以下各点:(0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)并用线段依次连接,看一看是什么图案.
y
x
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
9
10
5
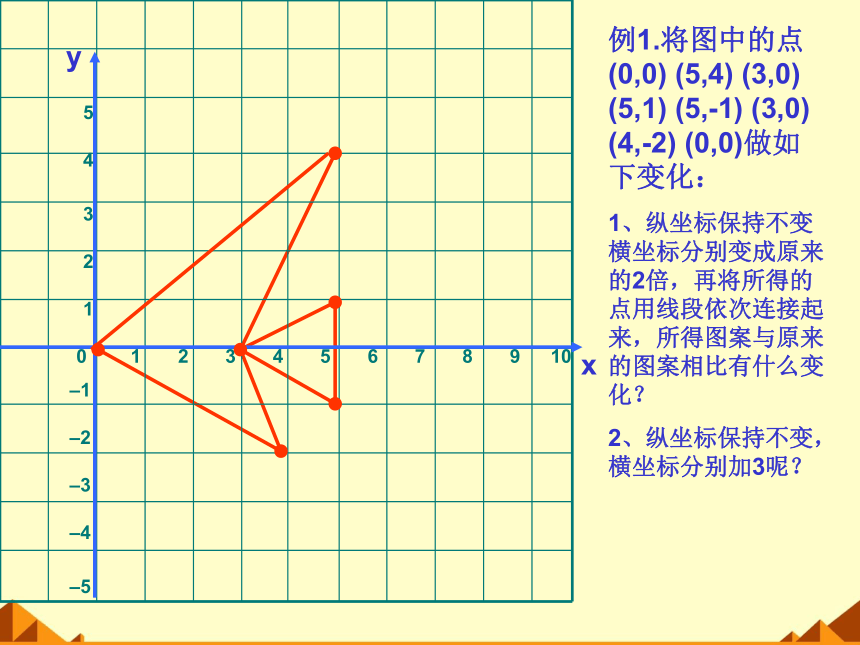
例1.将图中的点(0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)做如下变化:
1、纵坐标保持不变横坐标分别变成原来的2倍,再将所得的点用线段依次连接起来,所得图案与原来的图案相比有什么变化?
2、纵坐标保持不变,横坐标分别加3呢?
y
x
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
9
10
5
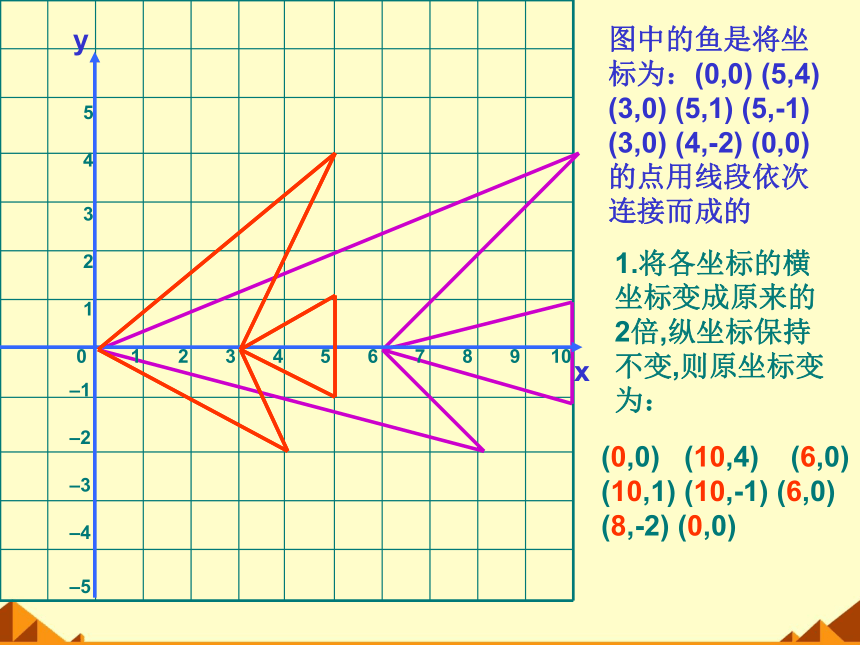
图中的鱼是将坐标为:(0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)的点用线段依次连接而成的
1.将各坐标的横坐标变成原来的2倍,纵坐标保持不变,则原坐标变为:
(0,0) (10,4) (6,0) (10,1) (10,-1) (6,0) (8,-2) (0,0)
y
x
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
9
10
5
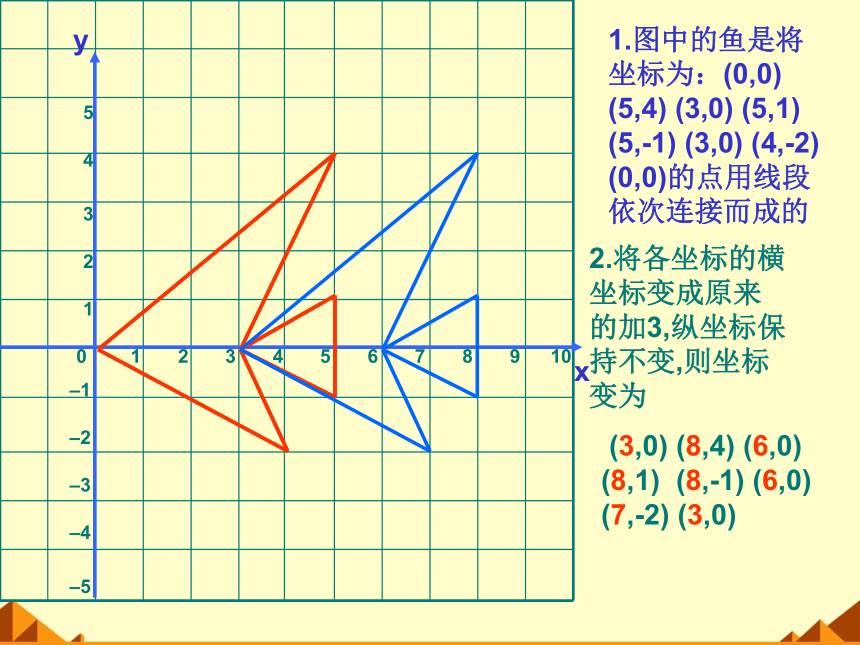
1.图中的鱼是将坐标为:(0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)的点用线段依次连接而成的
(3,0) (8,4) (6,0) (8,1) (8,-1) (6,0) (7,-2) (3,0)
2.将各坐标的横坐标变成原来的加3,纵坐标保持不变,则坐标变为
y
x
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
5
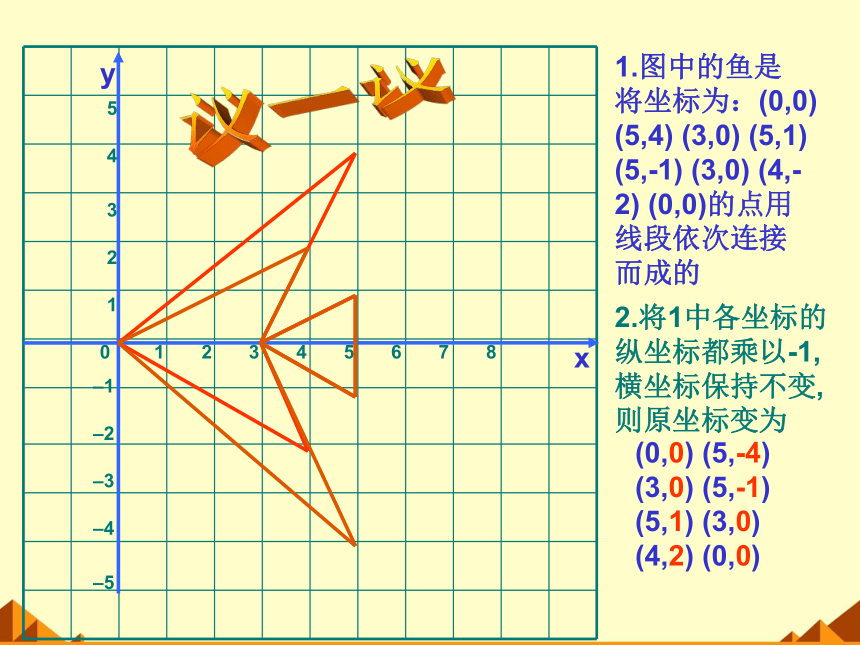
1.图中的鱼是将坐标为:(0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)的点用线段依次连接而成的
2.将1中各坐标的纵坐标都乘以-1,横坐标保持不变,则原坐标变为
(0,0) (5,-4) (3,0) (5,-1) (5,1) (3,0) (4,2) (0,0)
y
x
–4
1
2
3
4
5
6
7
8
0
–1
–2
–3
6
1
2
3
4
5
7
8
9
10
x
y
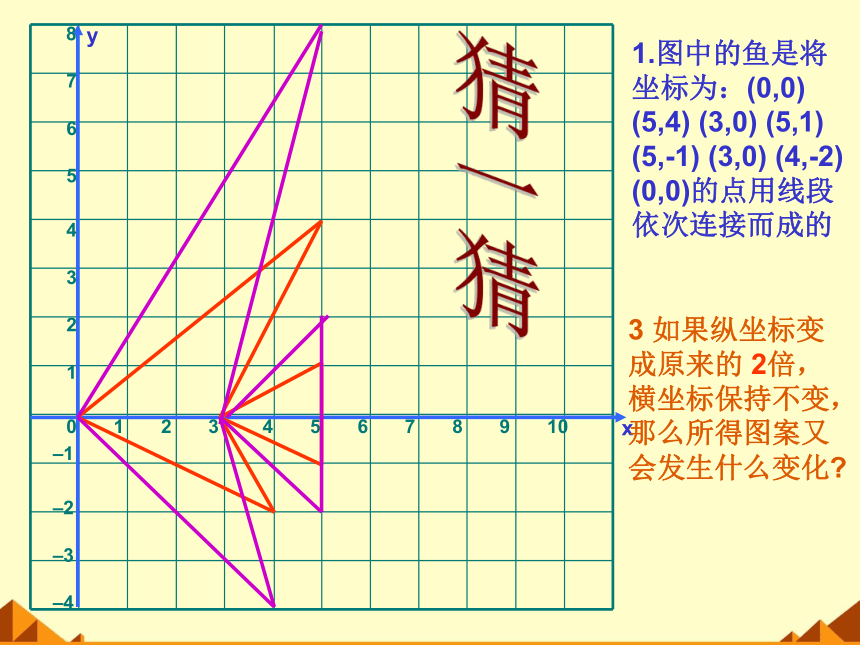
1.图中的鱼是将坐标为:(0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)的点用线段依次连接而成的
3 如果纵坐标变成原来的 2倍,横坐标保持不变,那么所得图案又会发生什么变化
–5
1.图中的鱼是将坐标为:(0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)的点用线段依次连接而成的
2.将1中各坐标的横、纵坐标都乘以-1,则原坐标变为
y
x
2
3
4
5
1
0
–1
–2
–3
–4
1
2
3
4
5
–1
–2
–3
–4
–5
(0,0) (-5,-4) (-3,0) (-5,-1) (-5, 1) (-3,0) (-4,2) (0,0)
1
2
3
4
1
0
4
3
2
–2
–1
–1
–2
–3
–4
–3
–4
1
2
3
4
1
0
4
3
2
–2
–1
–1
–2
–3
–4
–3
–4
与左图三角形相比,右图中的三角形发生了怎样变化。
右图中的直角三角形顶点的坐标发生怎样变化。
1
2
3
4
1
0
4
3
2
–2
–1
–1
–2
–3
–4
–3
–4
1
2
3
4
1
0
4
3
2
–2
–1
–1
–2
–3
–4
–3
–4
与左图三角形相比,右图中的三角形发生了怎样变化。
右图中的直角三角形顶点的坐标发生怎样变化。
1
2
3
4
1
0
4
3
2
–2
–1
–1
–2
–3
–4
–3
–4
1
2
3
4
1
0
4
3
2
–2
–1
–1
–2
–3
–4
–3
–4
与左图三角形相比,右图中的三角形发生了怎样变化。
右图中的直角三角形顶点的坐标发生怎样变化。
1
2
3
4
1
0
4
3
2
–2
–1
–1
–2
–3
–4
–3
–4
1
2
3
4
1
0
4
3
2
–2
–1
–1
–2
–3
–4
–3
–4
与左图三角形相比,右图中的三角形发生了怎样变化。
右图中的直角三角形顶点的坐标发生怎样变化。
1
2
3
4
1
0
4
3
2
–2
–1
–1
–2
–3
–4
–3
–4
1
2
3
4
1
0
4
3
2
–2
–1
–1
–2
–3
–4
–3
–4
与左图三角形相比,右图中的三角形发生了怎样变化。
右图中的直角三角形顶点的坐标发生怎样变化。
点的坐标变换引起图形的变化
点的坐标的平移变化——横、纵坐标加上一个正数
点的坐标的伸缩变化——横、纵坐标乘以一个正数
点的坐标关于X轴对称变化——纵坐标乘以-1
点的坐标关于Y轴对称变化——纵坐标乘以-1
点的坐标关于原点中心对称变化——横、纵坐标乘以-1
⑴平移:
(x,y) (x +a,y+b)
沿x轴方向平移a个单位,沿y轴方向平移b个单位;
⑵伸缩:
(x,y) (m x, ny)
沿x轴方向伸缩m倍,沿y轴方向伸缩n倍;
⑶放大缩小:
(x,y) (k x, ky)
形状不变,放大或缩小k倍;
⑷对称:
(x,y) (- x, y)
(x,y) (x, - y)
关于y轴对称;
关于x 轴对称;
–4
1
2
3
4
5
6
7
8
0
–1
–2
–3
6
1
2
3
4
5
7
8
9
10
x
y
如果纵坐标乘以2再加上3 ,横坐标不变,那么所得图案会发生什么变化
变化中的鱼
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
9
10
5
在直角坐标系中描出以下各点:(0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)并用线段依次连接,看一看是什么图案.
y
x
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
9
10
5
例1.将图中的点(0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)做如下变化:
1、纵坐标保持不变横坐标分别变成原来的2倍,再将所得的点用线段依次连接起来,所得图案与原来的图案相比有什么变化?
2、纵坐标保持不变,横坐标分别加3呢?
y
x
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
9
10
5
图中的鱼是将坐标为:(0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)的点用线段依次连接而成的
1.将各坐标的横坐标变成原来的2倍,纵坐标保持不变,则原坐标变为:
(0,0) (10,4) (6,0) (10,1) (10,-1) (6,0) (8,-2) (0,0)
y
x
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
9
10
5
1.图中的鱼是将坐标为:(0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)的点用线段依次连接而成的
(3,0) (8,4) (6,0) (8,1) (8,-1) (6,0) (7,-2) (3,0)
2.将各坐标的横坐标变成原来的加3,纵坐标保持不变,则坐标变为
y
x
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
5
1.图中的鱼是将坐标为:(0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)的点用线段依次连接而成的
2.将1中各坐标的纵坐标都乘以-1,横坐标保持不变,则原坐标变为
(0,0) (5,-4) (3,0) (5,-1) (5,1) (3,0) (4,2) (0,0)
y
x
–4
1
2
3
4
5
6
7
8
0
–1
–2
–3
6
1
2
3
4
5
7
8
9
10
x
y
1.图中的鱼是将坐标为:(0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)的点用线段依次连接而成的
3 如果纵坐标变成原来的 2倍,横坐标保持不变,那么所得图案又会发生什么变化
–5
1.图中的鱼是将坐标为:(0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)的点用线段依次连接而成的
2.将1中各坐标的横、纵坐标都乘以-1,则原坐标变为
y
x
2
3
4
5
1
0
–1
–2
–3
–4
1
2
3
4
5
–1
–2
–3
–4
–5
(0,0) (-5,-4) (-3,0) (-5,-1) (-5, 1) (-3,0) (-4,2) (0,0)
1
2
3
4
1
0
4
3
2
–2
–1
–1
–2
–3
–4
–3
–4
1
2
3
4
1
0
4
3
2
–2
–1
–1
–2
–3
–4
–3
–4
与左图三角形相比,右图中的三角形发生了怎样变化。
右图中的直角三角形顶点的坐标发生怎样变化。
1
2
3
4
1
0
4
3
2
–2
–1
–1
–2
–3
–4
–3
–4
1
2
3
4
1
0
4
3
2
–2
–1
–1
–2
–3
–4
–3
–4
与左图三角形相比,右图中的三角形发生了怎样变化。
右图中的直角三角形顶点的坐标发生怎样变化。
1
2
3
4
1
0
4
3
2
–2
–1
–1
–2
–3
–4
–3
–4
1
2
3
4
1
0
4
3
2
–2
–1
–1
–2
–3
–4
–3
–4
与左图三角形相比,右图中的三角形发生了怎样变化。
右图中的直角三角形顶点的坐标发生怎样变化。
1
2
3
4
1
0
4
3
2
–2
–1
–1
–2
–3
–4
–3
–4
1
2
3
4
1
0
4
3
2
–2
–1
–1
–2
–3
–4
–3
–4
与左图三角形相比,右图中的三角形发生了怎样变化。
右图中的直角三角形顶点的坐标发生怎样变化。
1
2
3
4
1
0
4
3
2
–2
–1
–1
–2
–3
–4
–3
–4
1
2
3
4
1
0
4
3
2
–2
–1
–1
–2
–3
–4
–3
–4
与左图三角形相比,右图中的三角形发生了怎样变化。
右图中的直角三角形顶点的坐标发生怎样变化。
点的坐标变换引起图形的变化
点的坐标的平移变化——横、纵坐标加上一个正数
点的坐标的伸缩变化——横、纵坐标乘以一个正数
点的坐标关于X轴对称变化——纵坐标乘以-1
点的坐标关于Y轴对称变化——纵坐标乘以-1
点的坐标关于原点中心对称变化——横、纵坐标乘以-1
⑴平移:
(x,y) (x +a,y+b)
沿x轴方向平移a个单位,沿y轴方向平移b个单位;
⑵伸缩:
(x,y) (m x, ny)
沿x轴方向伸缩m倍,沿y轴方向伸缩n倍;
⑶放大缩小:
(x,y) (k x, ky)
形状不变,放大或缩小k倍;
⑷对称:
(x,y) (- x, y)
(x,y) (x, - y)
关于y轴对称;
关于x 轴对称;
–4
1
2
3
4
5
6
7
8
0
–1
–2
–3
6
1
2
3
4
5
7
8
9
10
x
y
如果纵坐标乘以2再加上3 ,横坐标不变,那么所得图案会发生什么变化
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
