椭圆的标准方程
图片预览




文档简介
(共26张PPT)
椭圆的标准方程
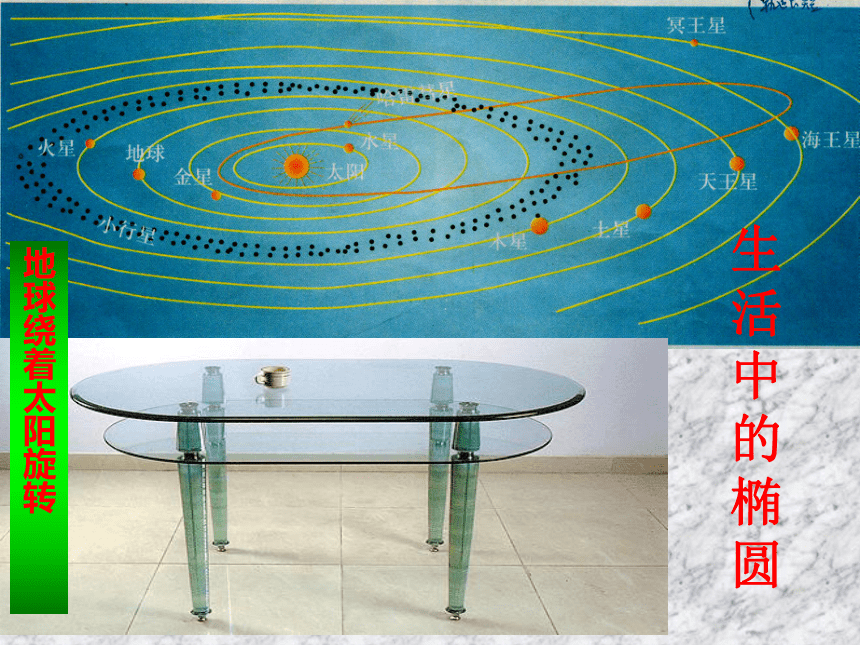
生活中的椭圆
地球绕着太阳旋转
压扁
将一个圆进行均匀压缩变形后,所得的图形也像椭圆.
椭圆?
如何精确地设计、制作、建造出现实生活中这些椭圆形的物件呢?
生活中的椭圆
一.问题情境
教学目标:
1.掌握椭圆的标准方程,能根据已知条件求椭圆的标准方程。
2.能用标准方程判定曲线是否是椭圆。
问题1:它们是不是数学概念上
的椭圆?怎样定义数学
上的椭圆?
问题2:如何建立椭圆的方程?
椭圆定义
求曲线方程
检查自学效果
请大家到课本中寻找
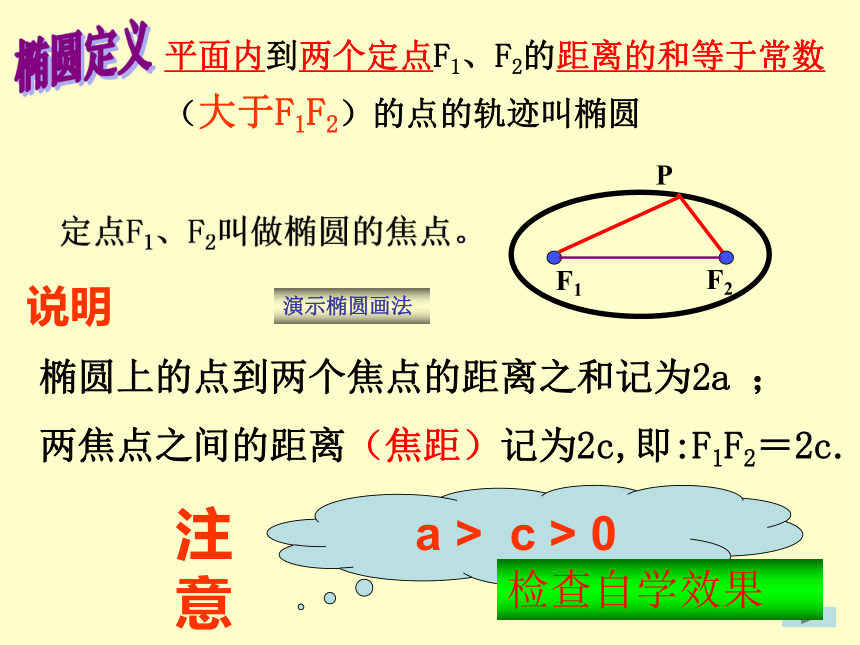
平面内到两个定点F1、F2的距离的和等于常数
(大于F1F2)的点的轨迹叫椭圆
定点F1、F2叫做椭圆的焦点。
F1
F2
P
椭圆上的点到两个焦点的距离之和记为2a ;
两焦点之间的距离(焦距)记为2c,即:F1F2=2c.
说明
注意
a > c > 0
检查自学效果
演示椭圆画法
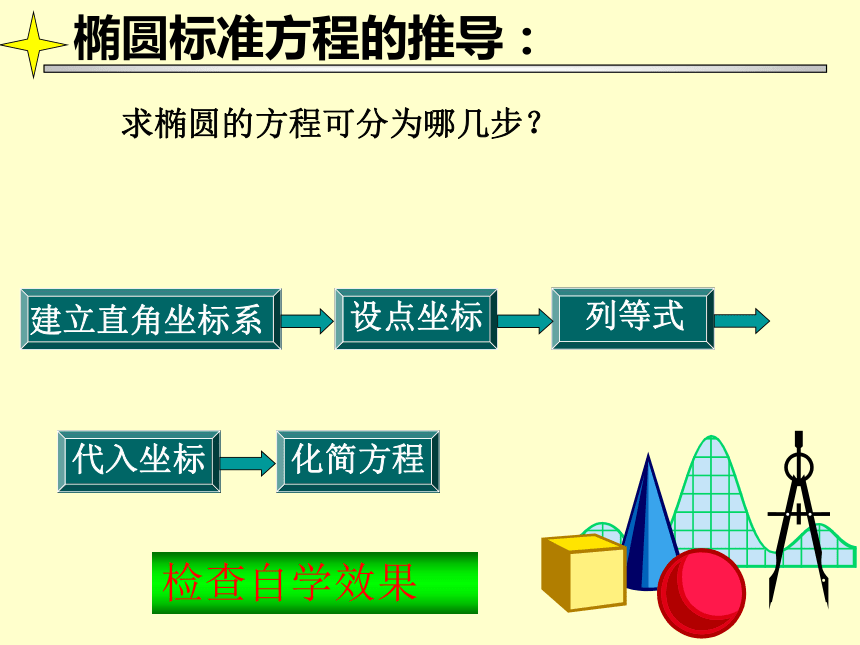
椭圆标准方程的推导:
建立直角坐标系
列等式
求椭圆的方程可分为哪几步?
设点坐标
代入坐标
化简方程
检查自学效果
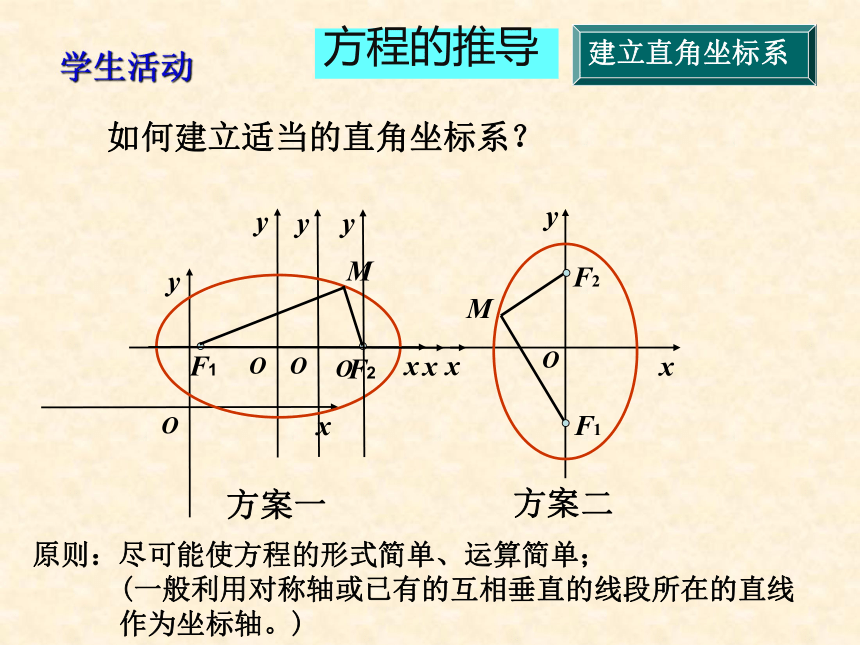
学生活动
O
x
y
O
x
y
O
x
y
M
F1
F2
方案一
F1
F2
方案二
O
x
y
M
O
x
y
原则:尽可能使方程的形式简单、运算简单;
(一般利用对称轴或已有的互相垂直的线段所在的直线
作为坐标轴。)
如何建立适当的直角坐标系?
建立直角坐标系
方程的推导
y
x
o
·
F1
·
F2
P
以直线F1F2为x轴,线段F1F2的垂直平分线为y轴,建立如图坐标系。
化简方程
建立直角坐标系
设点坐标
代入坐标
列等式
F1F2 = 2c
检查自学效果
方程的推导
y
x
o
·
F1
·
F2
P
设P(x,y)为椭圆上的任意一点,
∵F1F2=2c(c>0),
则:F1(-c,0)、F2(c,0)
以直线F1F2为x轴,线段F1F2的垂直平分线为y轴,建立如图坐标系。
化简方程
建立直角坐标系
设点坐标
代入坐标
列等式
方程的推导
∴
∴
∴
∴
设
∴
则,椭圆的方程为:
化简方程
建立直角坐标系
设点坐标
代入坐标
列等式
方程的推导
方程的推导
P
F2
F1
o
y
x
以直线F1F2为y轴,线段F1F2的垂直平分线为x轴,建立坐标系。
方程的推导
P
F2
F1
o
y
x
设P(x,y)为椭圆上的任意一点,
∵F1F2=2c(c>0),
则:F1(0,-c)、F2(0,c)
∵
∴
总体印象:对称、简洁,“像”直线方程的截距式
焦点在y轴:
焦点在x轴:
2)椭圆的标准方程
1
o
F
y
x
2
F
M
1
2
y
o
F
F
M
x
检查自学效果
a为最大,且满足
图 形
方 程
焦 点
F(±c,0)
F(0,±c)
a,b,c之间的关系
c2=a2-b2
MF1+MF2=2a (2a>2c>0)
定 义
1
2
y
o
F
F
M
x
1
o
F
y
x
2
F
M
3)两类标准方程的对照表
注:
共同点:椭圆的标准方程表示的一定是焦点在坐标轴上,中心在坐标原点的椭圆;方程的左边是平方和,右边是1.
不同点:焦点在x轴的椭圆 项分母较大.
焦点在y轴的椭圆 项分母较大.
1、已知椭圆的方程为:
则a=____,b=____,c=___, 焦点坐标为:___ ,焦距等于____。该椭圆上一点P到焦点F1的距离为8,则点P到另一个焦点F2的距离等于______。
10
6
8
(0,-8)、(0,8)
16
12
问题:已知椭圆的标准方程,如何判断焦点所在的坐标轴?
焦点在分母大的那个轴上
(1)两个焦点的坐标分别是(- 4,0)、(4,0),
椭圆上的一点P到焦点的距离的和等于10;
(2)两个焦点的坐标分别是(0,- 2),(0,2),
并且椭圆经过点(-3/2,5/2)。
F1
F2
M
x
y
O
x
y
o
F2
F1
M
表示焦点在x轴,焦点为
F1(-c,0),F2(c,0)
表示焦点在y轴,焦点为
F1(0, -c),F2(0, c)
求适合下列条件的椭圆的标准方程。
解:(1)因为椭圆的焦点在x轴上,故可设它的标准方程为
由已知,2a=10, 2c=8
故可得,a=5
c=4,b=3
求得椭圆的标准方程为:
(1)两个焦点的坐标分别是(- 4,0)、(4,0),
椭圆上的一点P到焦点的距离的和等于10;
(2)两个焦点的坐标分别是(0,- 2),(0,2),
并且椭圆经过点(-3/2,5/2)。
1、求适合下列条件的椭圆的标准方程。
解:(2)因椭圆的焦点在y轴上,故可设椭圆的标准方程为
由椭圆的定义与两点间距离公式可求得2a=
由已知,c=2,并可求得b=6
小结:求椭圆标准方程的步骤:
①定位:确定焦点所在的坐标轴;
②定量:求a, b的值.
例2、已知△ABC的一边BC固定,长为6,周长为16,
求顶点A的轨迹方程。
课堂练习
y
o
B
C
A
x
.
解:以BC的中点为原点,BC所在的直线为x轴建立直角坐标系。 根据椭圆的定义知所求轨迹方程是椭圆,且焦点在轴上,所以可设椭圆的标准方程为 :
∵ 2a=10, 2c=6
∴ a=5, c=3
∴ b2=a2-c2=52-32=16
∴所求椭圆的标准方程为
课堂练习:
课本106页1、2、3
练习题讲解
3. 标准方程的简单应用
一种方法(待定系数系法)
两种思想(数形结合、分类讨论)
1.两类方程(焦点分别在x轴,y轴上的标准方程)
2.椭圆标准方程焦点位置的判断方法:焦点在分母大的那个轴上
4 . F1、F2是椭圆的“定位”条件,决定了椭圆的类型,知道了焦点位置,椭圆的标准方程就确定了。若不知道了焦点的位置,椭圆的标准方程有两种形式。a,b确定了椭圆的形状和大小,是“定形”条件。
作业
1、教材P106页习题8.1第2,3,4题
2、预习椭圆的有关应用
3、观察以下两个椭圆,形状不同原因
在哪里?请大家改变绳长或变换焦
点位置再画椭圆进行研究.
76页练习1、解答:设两个定点A、B的长度为
以AB所在直线为x轴,以AB的中垂线为y轴,建立直角坐
标系,则A(-4,0)、B(4,0)
讲 评
练习题
A
y
o
B
M
x
.
∵椭圆的焦点在x轴上
∴设它的标准方程为:
∵ 2a=10, 2c=8
∴ a=5, c=4
∴ b2=a2-c2=52-42=9
∴所求椭圆的标准方程为
2、如果椭圆 上一点P到焦点F1的距离为6,则点P到另一焦点F2的距离为 。
14
3、说出适合下列条件的椭圆标准方程
(1) ,焦点在x 轴上;
(2) ,焦点在y 轴上。
(3)a+b=10,
椭圆的标准方程
生活中的椭圆
地球绕着太阳旋转
压扁
将一个圆进行均匀压缩变形后,所得的图形也像椭圆.
椭圆?
如何精确地设计、制作、建造出现实生活中这些椭圆形的物件呢?
生活中的椭圆
一.问题情境
教学目标:
1.掌握椭圆的标准方程,能根据已知条件求椭圆的标准方程。
2.能用标准方程判定曲线是否是椭圆。
问题1:它们是不是数学概念上
的椭圆?怎样定义数学
上的椭圆?
问题2:如何建立椭圆的方程?
椭圆定义
求曲线方程
检查自学效果
请大家到课本中寻找
平面内到两个定点F1、F2的距离的和等于常数
(大于F1F2)的点的轨迹叫椭圆
定点F1、F2叫做椭圆的焦点。
F1
F2
P
椭圆上的点到两个焦点的距离之和记为2a ;
两焦点之间的距离(焦距)记为2c,即:F1F2=2c.
说明
注意
a > c > 0
检查自学效果
演示椭圆画法
椭圆标准方程的推导:
建立直角坐标系
列等式
求椭圆的方程可分为哪几步?
设点坐标
代入坐标
化简方程
检查自学效果
学生活动
O
x
y
O
x
y
O
x
y
M
F1
F2
方案一
F1
F2
方案二
O
x
y
M
O
x
y
原则:尽可能使方程的形式简单、运算简单;
(一般利用对称轴或已有的互相垂直的线段所在的直线
作为坐标轴。)
如何建立适当的直角坐标系?
建立直角坐标系
方程的推导
y
x
o
·
F1
·
F2
P
以直线F1F2为x轴,线段F1F2的垂直平分线为y轴,建立如图坐标系。
化简方程
建立直角坐标系
设点坐标
代入坐标
列等式
F1F2 = 2c
检查自学效果
方程的推导
y
x
o
·
F1
·
F2
P
设P(x,y)为椭圆上的任意一点,
∵F1F2=2c(c>0),
则:F1(-c,0)、F2(c,0)
以直线F1F2为x轴,线段F1F2的垂直平分线为y轴,建立如图坐标系。
化简方程
建立直角坐标系
设点坐标
代入坐标
列等式
方程的推导
∴
∴
∴
∴
设
∴
则,椭圆的方程为:
化简方程
建立直角坐标系
设点坐标
代入坐标
列等式
方程的推导
方程的推导
P
F2
F1
o
y
x
以直线F1F2为y轴,线段F1F2的垂直平分线为x轴,建立坐标系。
方程的推导
P
F2
F1
o
y
x
设P(x,y)为椭圆上的任意一点,
∵F1F2=2c(c>0),
则:F1(0,-c)、F2(0,c)
∵
∴
总体印象:对称、简洁,“像”直线方程的截距式
焦点在y轴:
焦点在x轴:
2)椭圆的标准方程
1
o
F
y
x
2
F
M
1
2
y
o
F
F
M
x
检查自学效果
a为最大,且满足
图 形
方 程
焦 点
F(±c,0)
F(0,±c)
a,b,c之间的关系
c2=a2-b2
MF1+MF2=2a (2a>2c>0)
定 义
1
2
y
o
F
F
M
x
1
o
F
y
x
2
F
M
3)两类标准方程的对照表
注:
共同点:椭圆的标准方程表示的一定是焦点在坐标轴上,中心在坐标原点的椭圆;方程的左边是平方和,右边是1.
不同点:焦点在x轴的椭圆 项分母较大.
焦点在y轴的椭圆 项分母较大.
1、已知椭圆的方程为:
则a=____,b=____,c=___, 焦点坐标为:___ ,焦距等于____。该椭圆上一点P到焦点F1的距离为8,则点P到另一个焦点F2的距离等于______。
10
6
8
(0,-8)、(0,8)
16
12
问题:已知椭圆的标准方程,如何判断焦点所在的坐标轴?
焦点在分母大的那个轴上
(1)两个焦点的坐标分别是(- 4,0)、(4,0),
椭圆上的一点P到焦点的距离的和等于10;
(2)两个焦点的坐标分别是(0,- 2),(0,2),
并且椭圆经过点(-3/2,5/2)。
F1
F2
M
x
y
O
x
y
o
F2
F1
M
表示焦点在x轴,焦点为
F1(-c,0),F2(c,0)
表示焦点在y轴,焦点为
F1(0, -c),F2(0, c)
求适合下列条件的椭圆的标准方程。
解:(1)因为椭圆的焦点在x轴上,故可设它的标准方程为
由已知,2a=10, 2c=8
故可得,a=5
c=4,b=3
求得椭圆的标准方程为:
(1)两个焦点的坐标分别是(- 4,0)、(4,0),
椭圆上的一点P到焦点的距离的和等于10;
(2)两个焦点的坐标分别是(0,- 2),(0,2),
并且椭圆经过点(-3/2,5/2)。
1、求适合下列条件的椭圆的标准方程。
解:(2)因椭圆的焦点在y轴上,故可设椭圆的标准方程为
由椭圆的定义与两点间距离公式可求得2a=
由已知,c=2,并可求得b=6
小结:求椭圆标准方程的步骤:
①定位:确定焦点所在的坐标轴;
②定量:求a, b的值.
例2、已知△ABC的一边BC固定,长为6,周长为16,
求顶点A的轨迹方程。
课堂练习
y
o
B
C
A
x
.
解:以BC的中点为原点,BC所在的直线为x轴建立直角坐标系。 根据椭圆的定义知所求轨迹方程是椭圆,且焦点在轴上,所以可设椭圆的标准方程为 :
∵ 2a=10, 2c=6
∴ a=5, c=3
∴ b2=a2-c2=52-32=16
∴所求椭圆的标准方程为
课堂练习:
课本106页1、2、3
练习题讲解
3. 标准方程的简单应用
一种方法(待定系数系法)
两种思想(数形结合、分类讨论)
1.两类方程(焦点分别在x轴,y轴上的标准方程)
2.椭圆标准方程焦点位置的判断方法:焦点在分母大的那个轴上
4 . F1、F2是椭圆的“定位”条件,决定了椭圆的类型,知道了焦点位置,椭圆的标准方程就确定了。若不知道了焦点的位置,椭圆的标准方程有两种形式。a,b确定了椭圆的形状和大小,是“定形”条件。
作业
1、教材P106页习题8.1第2,3,4题
2、预习椭圆的有关应用
3、观察以下两个椭圆,形状不同原因
在哪里?请大家改变绳长或变换焦
点位置再画椭圆进行研究.
76页练习1、解答:设两个定点A、B的长度为
以AB所在直线为x轴,以AB的中垂线为y轴,建立直角坐
标系,则A(-4,0)、B(4,0)
讲 评
练习题
A
y
o
B
M
x
.
∵椭圆的焦点在x轴上
∴设它的标准方程为:
∵ 2a=10, 2c=8
∴ a=5, c=4
∴ b2=a2-c2=52-42=9
∴所求椭圆的标准方程为
2、如果椭圆 上一点P到焦点F1的距离为6,则点P到另一焦点F2的距离为 。
14
3、说出适合下列条件的椭圆标准方程
(1) ,焦点在x 轴上;
(2) ,焦点在y 轴上。
(3)a+b=10,
