黑龙江省大庆市龙凤区2021-2022学年九年级上学期期中考试数学试题(word版 含答案)
文档属性
| 名称 | 黑龙江省大庆市龙凤区2021-2022学年九年级上学期期中考试数学试题(word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 762.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-17 23:32:24 | ||
图片预览




文档简介
大庆市龙凤区2021-2022学年度第一学期初四年级第一次测试卷
数学试题
考生注意:
1. 考生将自己的姓名、准考证号填写到试卷和答题卡规定的位置。
2. 选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。
3. 非选择题用黑色墨水签字笔在答题卡上书写作答,在试题卷上作答无效。
4. 考试时间120分钟。
5. 全卷共28小题,总分120分。
选择题(本大题共10小题,每小题3分,共30分。在每小题所给出的四个选项中,只有一项是符合题目要求的,请将正确选项的序号填涂在答题卡上)
1.二次函数 y=-3(x+4)2+5的图象的开口方向、对称轴、顶点坐标分别是 ( )
A. 向上、直线 x=4,(4,5) B. 向上、直线 x= - 4,(-4,5)
C. 向下、直线 x=4,(4,-5) D. 向下、直线x= - 4,(-4,5)
2.抛物线y=x2﹣4x-m的图象经过点A(﹣3,y1),B(1,y2),C(4,y3),则y1,y2,y3大小关系是( )
A.y1<y2<y3 B.y1<y3<y2 C.y2<y3<y1 D.y3<y2<y1
3.如图,在 中,半径 于点 D,AD=4,则下列说法正确的是 ( )
A.OC=4 B.AB=8
C.OD=3 D.AB 垂直平分 OC
4.点 A(cos600 ,-tan300)关于原点对称的点A1 的坐标是 ( )
A. B. C. D.
5.在同一平面直角坐标中,直线y=ax+b与抛物线y=ax2+b的图象可能是( )
B. C. D.
6. 在矩形 ABCD 中,AB=8,,点 P 在边 AB 上,且 BP=3AP.如果圆 P 是以点 P 为圆心,PD 为半径的圆,那么下列判断正确的是 ( )
A. 点 B,C 均在圆 P 外
B. 点 B 在圆 P 外,点 C 在圆 P 内
C. 点 B 在圆 P 内,点 C 在圆 P 外
D. 点 B,C 均在圆 P 内
7.如图(3题下边)所示,在 中,斜边 AB=3,BC=1,点 D 在 AB 上,且 ,则 的值是 ( )
A. B. C. D.
A.3 B.4 C.5 D.6
10.如图是抛物线 图象的一部分,抛物线的顶点坐标 A(1,3),与 x 轴的一个交点 B(4,0),有下列结论:
① ;
② ;
③方程 有两个相等的实数根;
④当 时,,其中正确的是
A.②③ B.①③ C.①③④ D.①②③④
填空题(本大题共8小题,每小题3分,共24分。不需写出解答过程,请把答案直接填写在答题卡相应位置上)
11.若 ,则锐角
12.如图,在 中,,,则 的度数为
13.(12题下边)如图,某高速公路建设中需要测量某条江的宽度 AB,飞机上的测量人员在 C 处测得 A,B 两点的俯角分别为 450 和 300.若飞机离地面的高度 CH 为 1200 米,且点 H,A,B 在同一水平直线上,则这条江的宽度 AB 为 米(结果保留根号).
14.已知⊙O的半径为10,直线AB与⊙O相交,则圆心O到直线AB距离d的取值范围是 .
15.如图(12题下边),抛物线y=ax2+c与直线y=mx+n交于A(﹣1,p),
B(3,q)两点,则不等式ax2﹣mx+c<n的解集是 .
16.如图,把抛物线y=x2 沿直线 y=x 平移 个单位后,其顶点在直线上的 A 处,则平移后抛物线的表达式是 .
17.如图所示,小明在距离地面 30 m的 P 处测得 A 处的俯角为 150,B 处的俯角为 600,若斜坡 AB 的坡度为 ,则斜坡 AB 的长是
18.如图,平面直角坐标系中,分别A(-2,3)以点 ,B(3,4) 为圆心,以 1,3 为半径作 ,,M,N 分别是 , 上的动点,P 为 X 轴上的动点,则 PM+PN 的最小值等于 .
三、解答题(本大题共10小题,共66分。请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)
19、(6分)计算:(1)
(2)
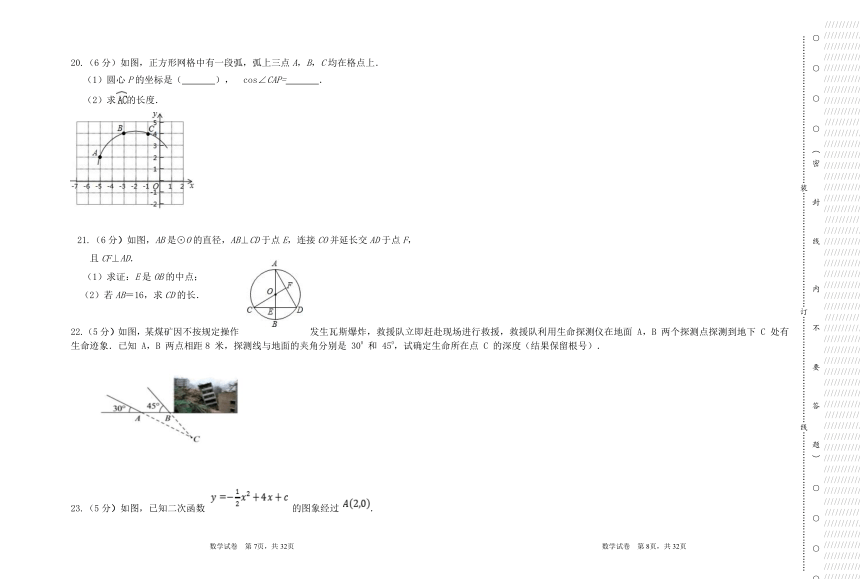
20.(6分)如图,正方形网格中有一段弧,弧上三点A,B,C均在格点上.
(1)圆心P的坐标是( ), cos∠CAP= .
(2)求的长度.
21.(6分)如图,AB是⊙O的直径,AB⊥CD于点E,连接CO并延长交AD于点F,
且CF⊥AD.
(1)求证:E是OB的中点;
(2)若AB=16,求CD的长.
22.(5分)如图,某煤矿因不按规定操作发生瓦斯爆炸,救援队立即赶赴现场进行救援,救援队利用生命探测仪在地面 A,B 两个探测点探测到地下 C 处有生命迹象.已知 A,B 两点相距8 米,探测线与地面的夹角分别是 300 和 450,试确定生命所在点 C 的深度(结果保留根号).
23.(5分)如图,已知二次函数 的图象经过 .
(1) 求 C 的值.
(2) 若二次函数与 Y 轴相交于 B 点,且该二次函数的对称轴与 X 轴交于点 C,连接 BA,BC,求 的面积.
24.(6分)如图,在半径为 5 的扇形 AOB 中,,点 C 是弧 AB 上的一个动点(不与点 A,B 重合),,,垂足分别为 D,E.
(1) 当 BC=6 时,求线段 OD 的长.
(2) 在 中是否存在长度保持不变的边?如果存在,请指出并求其长度;如果不存在,请说明理由.
25.(6分)如图所示,小杰发现垂直地面的旗杆AB 的影子落在地面和斜坡上,影长分别为BC 和CD ,经测量得BC=10 米,CD=10 米,斜坡CD 的坡度为i=1:3,且此时测得垂直于地面的1 米长的标杆在地面上的影长为 2米.求旗杆 AB的长度.(结果保留整数,其中3.2 )
26.(8分)如图,在Rt△ABC中,∠C=90°,AC、BC的长恰好为方程x2﹣14x+a=0的两根,且AC﹣BC=2,D为AB的中点.
(1)求a的值.
(2)动点P从点A出发,沿A→D→C的路线向点C运动;点Q从点B出发,沿B→C的路线向点C运动.若点P、Q同时出发,速度都为每秒2个单位,当点P经过点D时,点P速度变为每秒3单位,同时点Q速度变为每秒1个单位.当其中有一点到达终点时整个运动随之结束.设运动时间为t秒.在整个运动过程中,设△PCQ的面积为S,试求S与t之间的函数关系式;并指出自变量t的取值范围.
27.(9分)某商店经销一种双肩包,已知这种双肩包的成本价为每个 30 元,市场调查发现,这种双肩包每天的销售量 y(单位:个)与销售单价 x(单位:元)有如下关系:.设这种双肩包每天的销售利润为 ω 元.
(1) 求 ω 与 x 之间的函数表达式;
(2) 这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3) 如果物价部门规定这种双肩包的销售单价不高于 48 元,该商店销售这种双肩包每天要获得 200 元的销售利润,销售单价应定为多少元?
28.(9分)如图 1,抛物线 y=-x2+bx+c(a0) 与直线 y=x+1 相交于 A(-1,0)和B 两点,且抛物线经过点 C(5,0).
(1) 求抛物线的解析式.
(2) 点 P 是抛物线上的一个动点(不与点 A 点 B 重合),过点 P 作直线 轴于点 D,交直线 AB 于点 E.当 PE=2ED 时,求 P 点坐标.
(3) 如图 2 所示,设抛物线与 y 轴交于点 F,在抛物线的第一象限内,是否存在一点 Q,使得四边形 OFQC 的面积最大?若存在,请求出点 Q 的坐标;若不存在,说明理由.
龙凤区2021-2022学年第一学期初四年级第一次测试数学答案
一.选择题(本大题共10小题,每小题3分,共30分)
1~5 DCBAA 6~10 CCDCB
二.填空题(本大题共8小题,每小题3分,共24分。)
40 12. 300 13. (1200-1200 ) 14. 0 d <10
-118.
三、解答题(本大题共10小题,共66分。)
19.(1)原式=+×+×
=++
= .........3分
原式=2+1-2×+-1
=2 .....3分
20.(1)P(﹣2,1) 2分 ,cos∠CAP=; .........2分
(2)的长度为:=π. ......... 2分
21.(1)证明:连接AC,
∵直径AB垂直于弦CD于点E,
∴=,
∴AC=AD,
∵过圆心O的线CF⊥AD,
∴AF=DF,即CF是AD的中垂线,
∴AC=CD,
∴AC=AD=CD.
即:△ACD是等边三角形,
∴∠FCD=30°,
在Rt△COE中,OE=OC,
∴OE=OB,
∴点E为OB的中点; ......... 3分
(2)解:在Rt△OCE中,AB=16,
∴OC=AB=8,
又∵BE=OE,
∴OE=4,
∴CE===4,
∴CD=2CE=8. ......... 3分
22.【答案】 米.
【解析】作 交 的延长线于点 ,如右图所示,
由已知可得,
米,,,
,,
,
即 ,
解得, 米,
即生命所在点 的深度是 米.
......... 5分
23.(1) 把 代入 ,得 . ..2分
(2) 由 得 的坐标为 ,
,
抛物线对称轴为:,
点坐标为 ,
,
的面积为:. .......3分
24.(1) 如图 ,
,
,
,,,
,即线段 的长为 . ......3分
(2) 存在, 保持不变.
理由:连接 ,如图 ,
,,
,
,,
和 分别是线段 和 的中点,
,
保持不变. ......... 3分
25.
作DE⊥BC交BC延长线于E
∵ CD=10,i=1:3
∴DE=(米),CE=3(米)
作DF⊥AB垂足为F,易得DF=BC+CE=10+3(米)
由题意得
∴
∴AB=AF+BF=AF+DE=
∴旗杆AB的长度约为13米.........(6分)
26.解:(1)∵AC、BC的长为方程x2﹣14x+a=0的两根,
∴AC+BC=14,
又∵AC﹣BC=2,
∴AC=8,BC=6,
∴a=8×6=48; .........(3分)
(2)作PH⊥BC,垂足为H,
∵∠ACB=90°,
∴AB==10.
又∵D为AB的中点,
∴CD=AB=5. .........(1分)
当0≤t≤2.5时,
由PH∥AC得=,即=,
解得PH=(10﹣2t)
S=×CQ×PH=(6﹣2t)×(10﹣2t)=1.6t2﹣12.8t+24
........(2分)
当2.5<t<3.5时,
CQ=1﹣(t﹣2.5),PC=5﹣3(t﹣2.5),PH=(12.5﹣3t),
得S=1.2t2﹣t+.........(2分)
(1)
与 之间的函数表达式为 .(2分)(30x60)(1分)
(2) 根据题意得,.
,当 时, 有最大值,最大值是 .
即这种双肩包销售单价定为 元时,每天的销售利润最大,最大利润是 元. ........(3分)
(3) 当 时,,解得 ,.
,
不符合题意,舍去.
故该商店销售这种双肩包每天要获得 元的销售利润,销售单价应定为 元. ........(3分)
28.(1) 把 ,C 两点坐标代入抛物线解析式,
可得 解得
抛物线解析式为 . ........(2分)
(2) 设 ,则 ,,
则 ,,
,
当 时,解得 或 ,
但当 时, 与 重合不合题意,舍去,
;
当 时,解得 或 ,
但当 时, 与 重合不合题意,舍去,
.
综上可知, 点坐标为 或 .........(4分)
(3) 存在这样的点 ,使得四边形 的面积最大.
如图,过点 作 轴于点 ,
设 ,
则 ,,,
当 时,四边形 的面积取得最大值,最大值为 ,
此时点 的坐标为 . ........(3分)
3题
7题
8题
8
9.
15题
13题
12题
18题
17题
16题
24题
25题
数学试卷 第11页,共12页 数学试卷 第12页,共12页
数学试卷 第1页,共12页 数学试卷 第2页,共12页
数学试题
考生注意:
1. 考生将自己的姓名、准考证号填写到试卷和答题卡规定的位置。
2. 选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。
3. 非选择题用黑色墨水签字笔在答题卡上书写作答,在试题卷上作答无效。
4. 考试时间120分钟。
5. 全卷共28小题,总分120分。
选择题(本大题共10小题,每小题3分,共30分。在每小题所给出的四个选项中,只有一项是符合题目要求的,请将正确选项的序号填涂在答题卡上)
1.二次函数 y=-3(x+4)2+5的图象的开口方向、对称轴、顶点坐标分别是 ( )
A. 向上、直线 x=4,(4,5) B. 向上、直线 x= - 4,(-4,5)
C. 向下、直线 x=4,(4,-5) D. 向下、直线x= - 4,(-4,5)
2.抛物线y=x2﹣4x-m的图象经过点A(﹣3,y1),B(1,y2),C(4,y3),则y1,y2,y3大小关系是( )
A.y1<y2<y3 B.y1<y3<y2 C.y2<y3<y1 D.y3<y2<y1
3.如图,在 中,半径 于点 D,AD=4,则下列说法正确的是 ( )
A.OC=4 B.AB=8
C.OD=3 D.AB 垂直平分 OC
4.点 A(cos600 ,-tan300)关于原点对称的点A1 的坐标是 ( )
A. B. C. D.
5.在同一平面直角坐标中,直线y=ax+b与抛物线y=ax2+b的图象可能是( )
B. C. D.
6. 在矩形 ABCD 中,AB=8,,点 P 在边 AB 上,且 BP=3AP.如果圆 P 是以点 P 为圆心,PD 为半径的圆,那么下列判断正确的是 ( )
A. 点 B,C 均在圆 P 外
B. 点 B 在圆 P 外,点 C 在圆 P 内
C. 点 B 在圆 P 内,点 C 在圆 P 外
D. 点 B,C 均在圆 P 内
7.如图(3题下边)所示,在 中,斜边 AB=3,BC=1,点 D 在 AB 上,且 ,则 的值是 ( )
A. B. C. D.
A.3 B.4 C.5 D.6
10.如图是抛物线 图象的一部分,抛物线的顶点坐标 A(1,3),与 x 轴的一个交点 B(4,0),有下列结论:
① ;
② ;
③方程 有两个相等的实数根;
④当 时,,其中正确的是
A.②③ B.①③ C.①③④ D.①②③④
填空题(本大题共8小题,每小题3分,共24分。不需写出解答过程,请把答案直接填写在答题卡相应位置上)
11.若 ,则锐角
12.如图,在 中,,,则 的度数为
13.(12题下边)如图,某高速公路建设中需要测量某条江的宽度 AB,飞机上的测量人员在 C 处测得 A,B 两点的俯角分别为 450 和 300.若飞机离地面的高度 CH 为 1200 米,且点 H,A,B 在同一水平直线上,则这条江的宽度 AB 为 米(结果保留根号).
14.已知⊙O的半径为10,直线AB与⊙O相交,则圆心O到直线AB距离d的取值范围是 .
15.如图(12题下边),抛物线y=ax2+c与直线y=mx+n交于A(﹣1,p),
B(3,q)两点,则不等式ax2﹣mx+c<n的解集是 .
16.如图,把抛物线y=x2 沿直线 y=x 平移 个单位后,其顶点在直线上的 A 处,则平移后抛物线的表达式是 .
17.如图所示,小明在距离地面 30 m的 P 处测得 A 处的俯角为 150,B 处的俯角为 600,若斜坡 AB 的坡度为 ,则斜坡 AB 的长是
18.如图,平面直角坐标系中,分别A(-2,3)以点 ,B(3,4) 为圆心,以 1,3 为半径作 ,,M,N 分别是 , 上的动点,P 为 X 轴上的动点,则 PM+PN 的最小值等于 .
三、解答题(本大题共10小题,共66分。请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤)
19、(6分)计算:(1)
(2)
20.(6分)如图,正方形网格中有一段弧,弧上三点A,B,C均在格点上.
(1)圆心P的坐标是( ), cos∠CAP= .
(2)求的长度.
21.(6分)如图,AB是⊙O的直径,AB⊥CD于点E,连接CO并延长交AD于点F,
且CF⊥AD.
(1)求证:E是OB的中点;
(2)若AB=16,求CD的长.
22.(5分)如图,某煤矿因不按规定操作发生瓦斯爆炸,救援队立即赶赴现场进行救援,救援队利用生命探测仪在地面 A,B 两个探测点探测到地下 C 处有生命迹象.已知 A,B 两点相距8 米,探测线与地面的夹角分别是 300 和 450,试确定生命所在点 C 的深度(结果保留根号).
23.(5分)如图,已知二次函数 的图象经过 .
(1) 求 C 的值.
(2) 若二次函数与 Y 轴相交于 B 点,且该二次函数的对称轴与 X 轴交于点 C,连接 BA,BC,求 的面积.
24.(6分)如图,在半径为 5 的扇形 AOB 中,,点 C 是弧 AB 上的一个动点(不与点 A,B 重合),,,垂足分别为 D,E.
(1) 当 BC=6 时,求线段 OD 的长.
(2) 在 中是否存在长度保持不变的边?如果存在,请指出并求其长度;如果不存在,请说明理由.
25.(6分)如图所示,小杰发现垂直地面的旗杆AB 的影子落在地面和斜坡上,影长分别为BC 和CD ,经测量得BC=10 米,CD=10 米,斜坡CD 的坡度为i=1:3,且此时测得垂直于地面的1 米长的标杆在地面上的影长为 2米.求旗杆 AB的长度.(结果保留整数,其中3.2 )
26.(8分)如图,在Rt△ABC中,∠C=90°,AC、BC的长恰好为方程x2﹣14x+a=0的两根,且AC﹣BC=2,D为AB的中点.
(1)求a的值.
(2)动点P从点A出发,沿A→D→C的路线向点C运动;点Q从点B出发,沿B→C的路线向点C运动.若点P、Q同时出发,速度都为每秒2个单位,当点P经过点D时,点P速度变为每秒3单位,同时点Q速度变为每秒1个单位.当其中有一点到达终点时整个运动随之结束.设运动时间为t秒.在整个运动过程中,设△PCQ的面积为S,试求S与t之间的函数关系式;并指出自变量t的取值范围.
27.(9分)某商店经销一种双肩包,已知这种双肩包的成本价为每个 30 元,市场调查发现,这种双肩包每天的销售量 y(单位:个)与销售单价 x(单位:元)有如下关系:.设这种双肩包每天的销售利润为 ω 元.
(1) 求 ω 与 x 之间的函数表达式;
(2) 这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3) 如果物价部门规定这种双肩包的销售单价不高于 48 元,该商店销售这种双肩包每天要获得 200 元的销售利润,销售单价应定为多少元?
28.(9分)如图 1,抛物线 y=-x2+bx+c(a0) 与直线 y=x+1 相交于 A(-1,0)和B 两点,且抛物线经过点 C(5,0).
(1) 求抛物线的解析式.
(2) 点 P 是抛物线上的一个动点(不与点 A 点 B 重合),过点 P 作直线 轴于点 D,交直线 AB 于点 E.当 PE=2ED 时,求 P 点坐标.
(3) 如图 2 所示,设抛物线与 y 轴交于点 F,在抛物线的第一象限内,是否存在一点 Q,使得四边形 OFQC 的面积最大?若存在,请求出点 Q 的坐标;若不存在,说明理由.
龙凤区2021-2022学年第一学期初四年级第一次测试数学答案
一.选择题(本大题共10小题,每小题3分,共30分)
1~5 DCBAA 6~10 CCDCB
二.填空题(本大题共8小题,每小题3分,共24分。)
40 12. 300 13. (1200-1200 ) 14. 0 d <10
-1
三、解答题(本大题共10小题,共66分。)
19.(1)原式=+×+×
=++
= .........3分
原式=2+1-2×+-1
=2 .....3分
20.(1)P(﹣2,1) 2分 ,cos∠CAP=; .........2分
(2)的长度为:=π. ......... 2分
21.(1)证明:连接AC,
∵直径AB垂直于弦CD于点E,
∴=,
∴AC=AD,
∵过圆心O的线CF⊥AD,
∴AF=DF,即CF是AD的中垂线,
∴AC=CD,
∴AC=AD=CD.
即:△ACD是等边三角形,
∴∠FCD=30°,
在Rt△COE中,OE=OC,
∴OE=OB,
∴点E为OB的中点; ......... 3分
(2)解:在Rt△OCE中,AB=16,
∴OC=AB=8,
又∵BE=OE,
∴OE=4,
∴CE===4,
∴CD=2CE=8. ......... 3分
22.【答案】 米.
【解析】作 交 的延长线于点 ,如右图所示,
由已知可得,
米,,,
,,
,
即 ,
解得, 米,
即生命所在点 的深度是 米.
......... 5分
23.(1) 把 代入 ,得 . ..2分
(2) 由 得 的坐标为 ,
,
抛物线对称轴为:,
点坐标为 ,
,
的面积为:. .......3分
24.(1) 如图 ,
,
,
,,,
,即线段 的长为 . ......3分
(2) 存在, 保持不变.
理由:连接 ,如图 ,
,,
,
,,
和 分别是线段 和 的中点,
,
保持不变. ......... 3分
25.
作DE⊥BC交BC延长线于E
∵ CD=10,i=1:3
∴DE=(米),CE=3(米)
作DF⊥AB垂足为F,易得DF=BC+CE=10+3(米)
由题意得
∴
∴AB=AF+BF=AF+DE=
∴旗杆AB的长度约为13米.........(6分)
26.解:(1)∵AC、BC的长为方程x2﹣14x+a=0的两根,
∴AC+BC=14,
又∵AC﹣BC=2,
∴AC=8,BC=6,
∴a=8×6=48; .........(3分)
(2)作PH⊥BC,垂足为H,
∵∠ACB=90°,
∴AB==10.
又∵D为AB的中点,
∴CD=AB=5. .........(1分)
当0≤t≤2.5时,
由PH∥AC得=,即=,
解得PH=(10﹣2t)
S=×CQ×PH=(6﹣2t)×(10﹣2t)=1.6t2﹣12.8t+24
........(2分)
当2.5<t<3.5时,
CQ=1﹣(t﹣2.5),PC=5﹣3(t﹣2.5),PH=(12.5﹣3t),
得S=1.2t2﹣t+.........(2分)
(1)
与 之间的函数表达式为 .(2分)(30x60)(1分)
(2) 根据题意得,.
,当 时, 有最大值,最大值是 .
即这种双肩包销售单价定为 元时,每天的销售利润最大,最大利润是 元. ........(3分)
(3) 当 时,,解得 ,.
,
不符合题意,舍去.
故该商店销售这种双肩包每天要获得 元的销售利润,销售单价应定为 元. ........(3分)
28.(1) 把 ,C 两点坐标代入抛物线解析式,
可得 解得
抛物线解析式为 . ........(2分)
(2) 设 ,则 ,,
则 ,,
,
当 时,解得 或 ,
但当 时, 与 重合不合题意,舍去,
;
当 时,解得 或 ,
但当 时, 与 重合不合题意,舍去,
.
综上可知, 点坐标为 或 .........(4分)
(3) 存在这样的点 ,使得四边形 的面积最大.
如图,过点 作 轴于点 ,
设 ,
则 ,,,
当 时,四边形 的面积取得最大值,最大值为 ,
此时点 的坐标为 . ........(3分)
3题
7题
8题
8
9.
15题
13题
12题
18题
17题
16题
24题
25题
数学试卷 第11页,共12页 数学试卷 第12页,共12页
数学试卷 第1页,共12页 数学试卷 第2页,共12页
同课章节目录
