北师大版八年级数学上册 第一章 勾股定理 复习课件(共38张PPT)
文档属性
| 名称 | 北师大版八年级数学上册 第一章 勾股定理 复习课件(共38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 785.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 14:22:04 | ||
图片预览






文档简介
(共38张PPT)
第一章 勾股定理 复习课件
A
R
C
P
Q
B
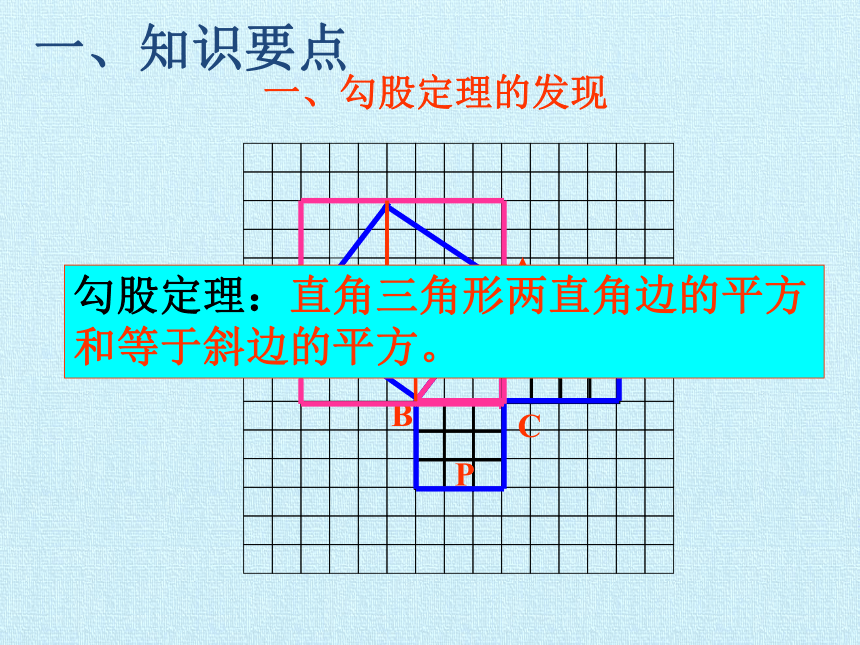
一、勾股定理的发现
勾股定理:直角三角形两直角边的平方和等于斜边的平方。
一、知识要点
如果直角三角形两直角边分别为a,b,斜边为c,那么:
勾股定理
a2+ b2=c2
即直角三角形两直角边的平方和等于斜边的平方。
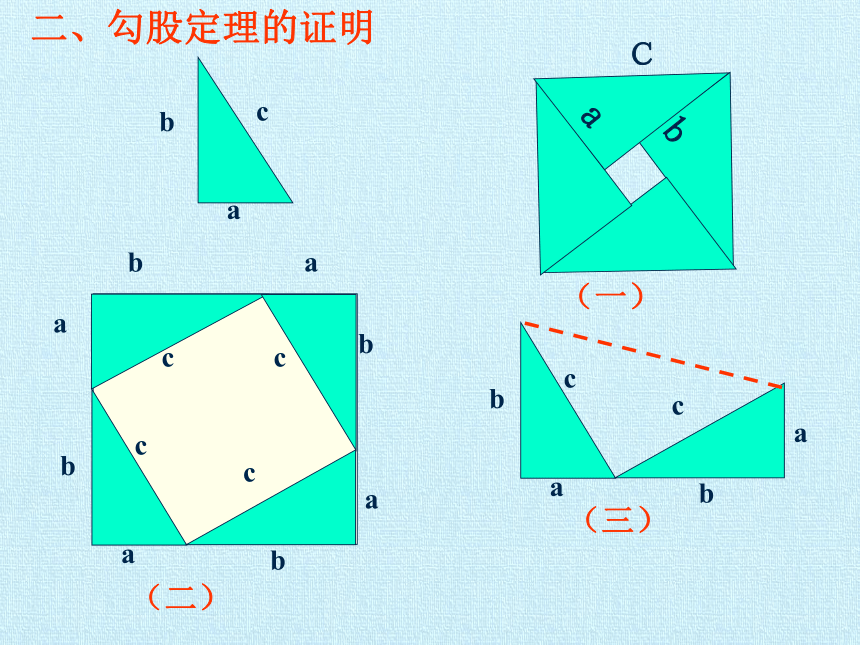
二、勾股定理的证明
c
c
a
a
b
b
c
c
a
a
b
b
b
a
c
C
a
b
c
c
a
a
b
b
(一)
(二)
(三)
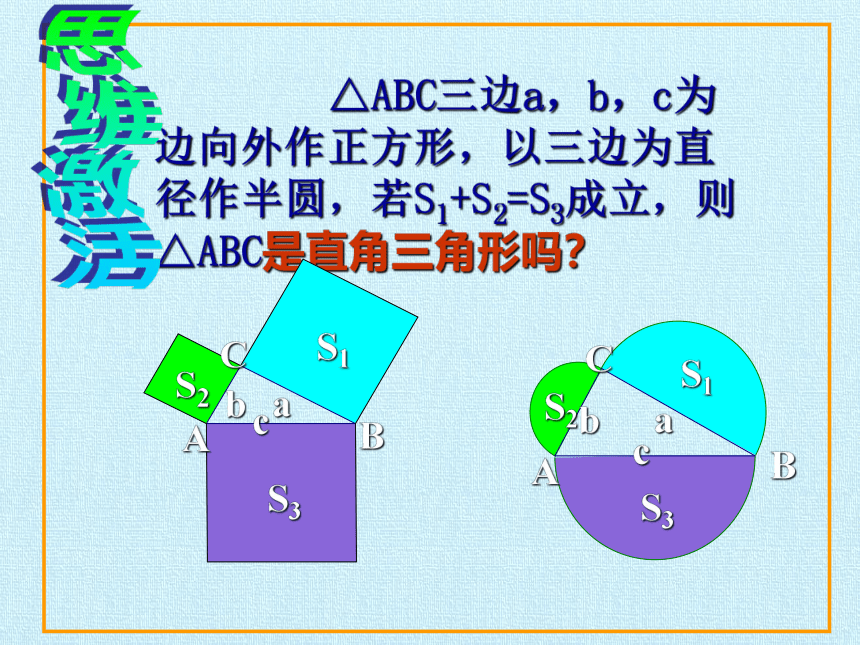
△ABC三边a,b,c为边向外作正方形,以三边为直径作半圆,若S1+S2=S3成立,则△ABC是直角三角形吗?
A
B
C
a
b
c
S1
S2
S3
思维激活
A
C
a
b
c
S1
S2
S3
B
S
S
S
C
B
A
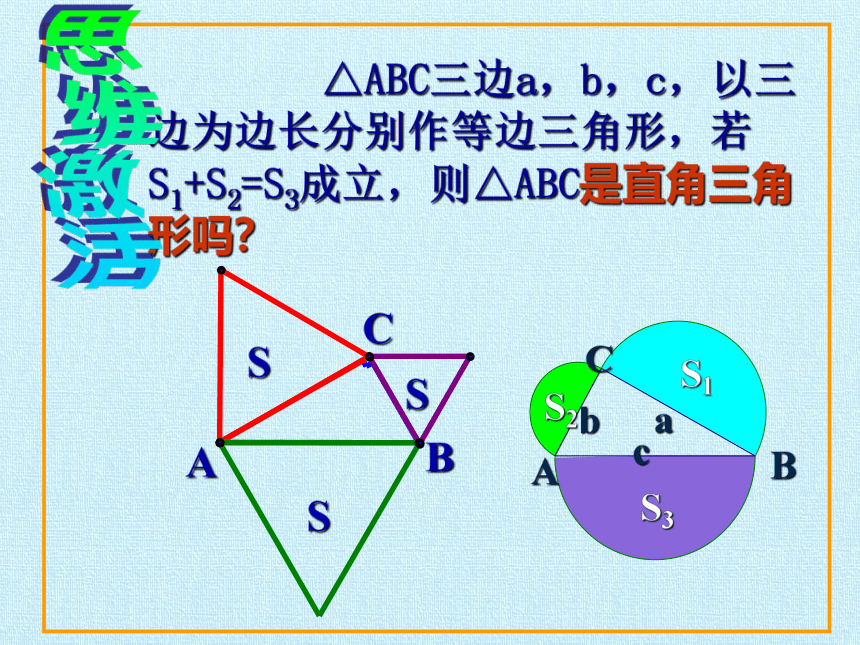
△ABC三边a,b,c,以三边为边长分别作等边三角形,若S1+S2=S3成立,则△ABC是直角三角形吗?
A
C
a
b
c
S1
S2
S3
思维激活
B
例1:在Rt△ABC中,∠C=90°。
(1)若a=3,b=4,则c= ;
(2)若c=34,a:b=8:15,则 a= ,b= ;
典型例题
5
16
30
A
B
C
a
b
c
勾股逆定理
如果三角形的三边长a,b,c满足a2 +b2=c2 ,
那么这个三角形是直角三角形。
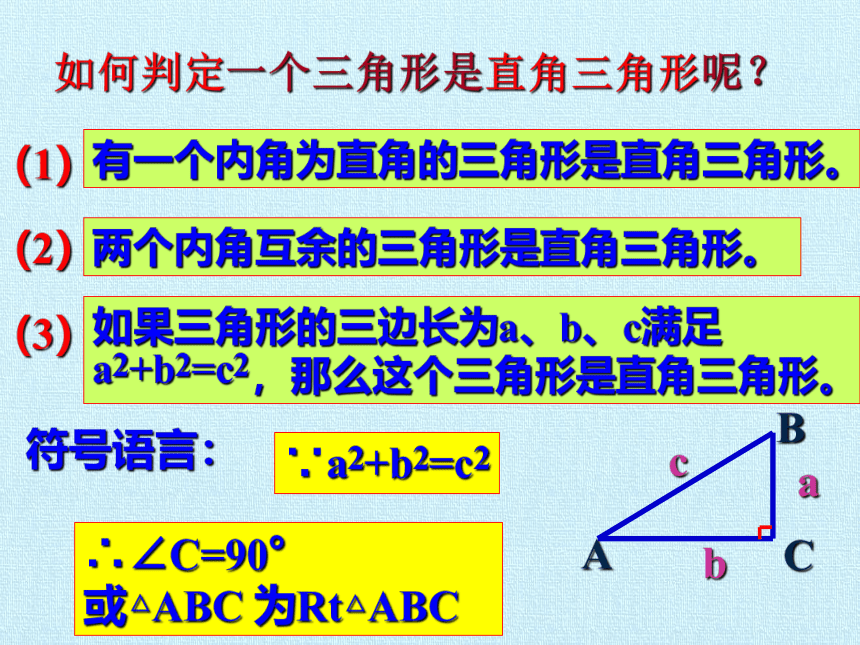
如何判定一个三角形是直角三角形呢?
(1)
(2)
有一个内角为直角的三角形是直角三角形。
两个内角互余的三角形是直角三角形。
符号语言:
∴∠C=90°
或△ABC 为Rt△ABC
∵a2+b2=c2
(3)
如果三角形的三边长为a、b、c满足
a2+b2=c2,那么这个三角形是直角三角形。
C
A
B
a
b
c
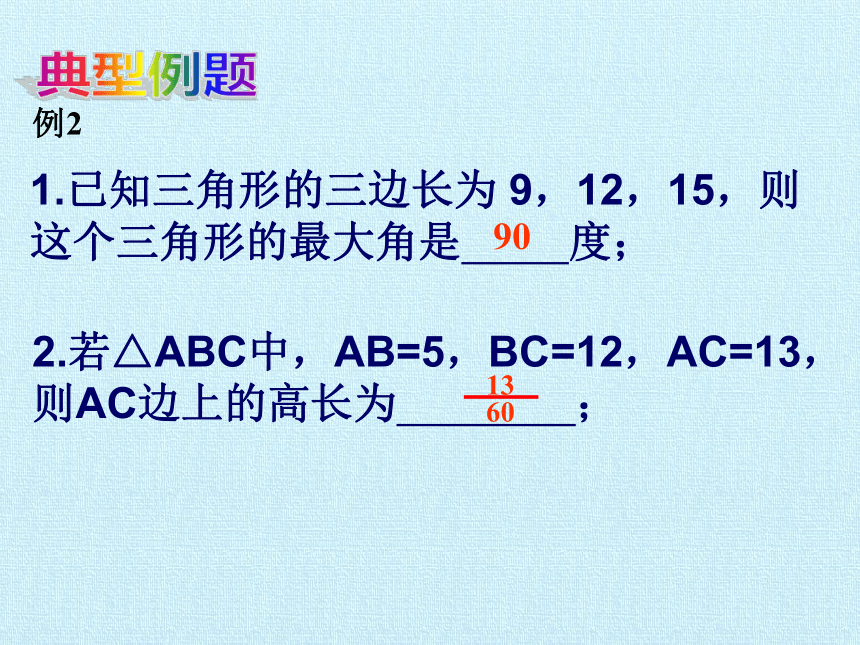
典型例题
1.已知三角形的三边长为 9,12,15,则这个三角形的最大角是 度;
2.若△ABC中,AB=5,BC=12,AC=13,则AC边上的高长为 ;
例2
90
13
60
有四个三角形,分别满足下列条件:
①一个内角等于另两个内角之和;
②三个角之比为3:4:5;
③三边长分别为7、24、25
④三边之比为5:12:13
其中直角三角形有( )
A、1个 B、2个 C、3个 D、4个
C
勾股数
满足a2 +b2=c2的三个正整数,称为勾股数。
例3.请完成以下未完成的勾股数:
(1)8、15、_______;
(2)10、26、_____;
(3) 7、 _____ 、25。
典型例题
17
24
24
例4.观察下列表格:
列举 猜想
3、4、5 32=4+5
5、12、13 52=12+13
7、24、25 72=24+25
…… ……
13、b、c 132=b+c
请你结合该表格及相关知识,求出b、c的值。即b= ,c=________。
84
85
例5.如图,四边形ABCD中,AB=3,BC=4,CD=12,AD=13,∠B=90°,求四边形ABCD的面积。
┐
D
B
A
C
典型例题
3
4
12
13
变式:有一块田地的形状和尺寸如图所示,试求它的面积。
∟
∟
A
B
C
D
5
例6.假期中,王强和同学到某海岛上去玩探宝游戏,按照探宝图,他们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,在折向北走到6千米处往东一拐,仅走1千米就找到宝藏,问登陆点A 到宝藏埋藏点B的距离是多少千米?
A
B
8
2
3
6
1
M
N
17
规律
专题一 分类思想
1.直角三角形中,已知两边长是直角边、斜边不知道时,应分类讨论。
2.当已知条件中没有给出图形时,应认真读句画图,避免遗漏另一种情况。
∟
D
2.三角形ABC中,AB=10,AC=17,BC边上的高线AD=8,求BC。
∟
D
A
B
C
1.已知:直角三角形的三边长分别是3,4,X,则X2=__________。
25
或7
A
B
C
10
17
8
17
10
8
专题二 方程思想
直角三角形中,当无法已知两边求第三边时,应采用间接求法:灵活地寻找题中的等量关系,利用勾股定理列方程。
规律
1.小东拿着一根长竹竿进一个宽为3米的城门,他先横拿着进不去,又竖起来拿,结果竹竿比城门高1米,当他把竹竿斜着时,两端刚好顶着城门的对角,问竹竿长多少?
练习:
x
1m
(x+1)
3
在一棵树的10米高处B有两只猴子,其中一只猴子爬下树走到离树20米的池塘A,另一只猴子爬到树顶D后直接跃向池塘的A处,如果两只猴子所经过距离相等,试问这棵树有多高?
.
D
B
C
A
专题三 折叠
折叠和轴对称密不可分,利用折叠前后图形全等,找到对应边、对应角相等便可顺利解决折叠问题。
规律
例1.如图,一块直角三角形的纸片,两直角边AC=6㎝,BC=8㎝。现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长。
A
C
D
B
E
第8题图
D
x
6
x
8-x
4
6
8
练习:三角形ABC是等腰三角形AB=AC=13,BC=10,将AB向AC方向对折,再将CD折叠到CA边上,折痕CE,求三角形ACE的面积。
A
B
C
D
A
D
C
D
C
A
D1
E
13
5
12
5
12-x
5
x
x
8
例2.折叠矩形ABCD的一边AD,点D落在BC边上的点F处,已知AB=8CM,BC=10CM,求:1.CF 2.EC。
A
B
C
D
E
F
8
10
10
X
8-X
4
8-X
6
1. 几何体的表面路径最短的问题,一般展开表面成平面。
2.利用两点之间线段最短,及勾股定理求解。
专题四 展开思想
规律
例1:如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程 (取3)是( )
A.20cm B.10cm C.14cm D.无法确定
B
B
8
O
A
2
蛋糕
A
C
B
8
周长的一半
6
例2:如图,正方体的棱长为5cm,一只蚂蚁欲从正方体底面上的顶点A沿正方体的表面到顶点C′处吃食物,那么它需要爬行的最短路程的长是多少?
A
B
C
D′
A′
B′
C′
D
例3:如图是一个三级台阶,它的每一级的长宽和高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点最短路程是多少?
20
3
2
A
B
20
2
3
2
3
2
3
A
B
C
∵ AB2=AC2+BC2=625,
∴ AB=25。
例4:如图,长方体的长为15cm,宽为10 cm,高为20cm,点B离点C5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是多少?
10
20
B
A
C
15
5
10
20
B
5
B
5
10
20
A
C
E
F
E
10
20
A
C
F
A
E
C
B
20
15
10
5
1.几何体的内部路径最值的问题,一般画出几何体截面。
2.利用两点之间线段最短及勾股定理求解。
专题五 截面中的勾股定理
规律
小明家住在18层的高楼,一天,他与妈妈去买竹竿。
买最长的吧!
快点回家,好用它凉衣服。
糟糕,太长了,放不进去。
如果电梯的长、宽、高分别是1.5米、1.5米、2.2米,那么,能放入电梯内的竹竿的最大长度大约是多少米?你能估计出小明买的竹竿至少是多少米吗?
1.5米
1.5米
2.2米
1.5米
1.5米
x
x
2.2米
A
B
C
X2=1.52+1.52=4.5
AB2=2.22+X2=9.34
AB≈3米
练习:一种盛饮料的圆柱形杯,测得内部底面半径为2.5㎝,高为12㎝,吸管放进杯里,杯口外面至少要露出4.6㎝,问吸管要做多长?
感悟与反思
1、通过这节课的学习活动你有哪些收获?
2、对这节课的学习,你还有什么想法吗?
谢 谢
第一章 勾股定理 复习课件
A
R
C
P
Q
B
一、勾股定理的发现
勾股定理:直角三角形两直角边的平方和等于斜边的平方。
一、知识要点
如果直角三角形两直角边分别为a,b,斜边为c,那么:
勾股定理
a2+ b2=c2
即直角三角形两直角边的平方和等于斜边的平方。
二、勾股定理的证明
c
c
a
a
b
b
c
c
a
a
b
b
b
a
c
C
a
b
c
c
a
a
b
b
(一)
(二)
(三)
△ABC三边a,b,c为边向外作正方形,以三边为直径作半圆,若S1+S2=S3成立,则△ABC是直角三角形吗?
A
B
C
a
b
c
S1
S2
S3
思维激活
A
C
a
b
c
S1
S2
S3
B
S
S
S
C
B
A
△ABC三边a,b,c,以三边为边长分别作等边三角形,若S1+S2=S3成立,则△ABC是直角三角形吗?
A
C
a
b
c
S1
S2
S3
思维激活
B
例1:在Rt△ABC中,∠C=90°。
(1)若a=3,b=4,则c= ;
(2)若c=34,a:b=8:15,则 a= ,b= ;
典型例题
5
16
30
A
B
C
a
b
c
勾股逆定理
如果三角形的三边长a,b,c满足a2 +b2=c2 ,
那么这个三角形是直角三角形。
如何判定一个三角形是直角三角形呢?
(1)
(2)
有一个内角为直角的三角形是直角三角形。
两个内角互余的三角形是直角三角形。
符号语言:
∴∠C=90°
或△ABC 为Rt△ABC
∵a2+b2=c2
(3)
如果三角形的三边长为a、b、c满足
a2+b2=c2,那么这个三角形是直角三角形。
C
A
B
a
b
c
典型例题
1.已知三角形的三边长为 9,12,15,则这个三角形的最大角是 度;
2.若△ABC中,AB=5,BC=12,AC=13,则AC边上的高长为 ;
例2
90
13
60
有四个三角形,分别满足下列条件:
①一个内角等于另两个内角之和;
②三个角之比为3:4:5;
③三边长分别为7、24、25
④三边之比为5:12:13
其中直角三角形有( )
A、1个 B、2个 C、3个 D、4个
C
勾股数
满足a2 +b2=c2的三个正整数,称为勾股数。
例3.请完成以下未完成的勾股数:
(1)8、15、_______;
(2)10、26、_____;
(3) 7、 _____ 、25。
典型例题
17
24
24
例4.观察下列表格:
列举 猜想
3、4、5 32=4+5
5、12、13 52=12+13
7、24、25 72=24+25
…… ……
13、b、c 132=b+c
请你结合该表格及相关知识,求出b、c的值。即b= ,c=________。
84
85
例5.如图,四边形ABCD中,AB=3,BC=4,CD=12,AD=13,∠B=90°,求四边形ABCD的面积。
┐
D
B
A
C
典型例题
3
4
12
13
变式:有一块田地的形状和尺寸如图所示,试求它的面积。
∟
∟
A
B
C
D
5
例6.假期中,王强和同学到某海岛上去玩探宝游戏,按照探宝图,他们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,在折向北走到6千米处往东一拐,仅走1千米就找到宝藏,问登陆点A 到宝藏埋藏点B的距离是多少千米?
A
B
8
2
3
6
1
M
N
17
规律
专题一 分类思想
1.直角三角形中,已知两边长是直角边、斜边不知道时,应分类讨论。
2.当已知条件中没有给出图形时,应认真读句画图,避免遗漏另一种情况。
∟
D
2.三角形ABC中,AB=10,AC=17,BC边上的高线AD=8,求BC。
∟
D
A
B
C
1.已知:直角三角形的三边长分别是3,4,X,则X2=__________。
25
或7
A
B
C
10
17
8
17
10
8
专题二 方程思想
直角三角形中,当无法已知两边求第三边时,应采用间接求法:灵活地寻找题中的等量关系,利用勾股定理列方程。
规律
1.小东拿着一根长竹竿进一个宽为3米的城门,他先横拿着进不去,又竖起来拿,结果竹竿比城门高1米,当他把竹竿斜着时,两端刚好顶着城门的对角,问竹竿长多少?
练习:
x
1m
(x+1)
3
在一棵树的10米高处B有两只猴子,其中一只猴子爬下树走到离树20米的池塘A,另一只猴子爬到树顶D后直接跃向池塘的A处,如果两只猴子所经过距离相等,试问这棵树有多高?
.
D
B
C
A
专题三 折叠
折叠和轴对称密不可分,利用折叠前后图形全等,找到对应边、对应角相等便可顺利解决折叠问题。
规律
例1.如图,一块直角三角形的纸片,两直角边AC=6㎝,BC=8㎝。现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长。
A
C
D
B
E
第8题图
D
x
6
x
8-x
4
6
8
练习:三角形ABC是等腰三角形AB=AC=13,BC=10,将AB向AC方向对折,再将CD折叠到CA边上,折痕CE,求三角形ACE的面积。
A
B
C
D
A
D
C
D
C
A
D1
E
13
5
12
5
12-x
5
x
x
8
例2.折叠矩形ABCD的一边AD,点D落在BC边上的点F处,已知AB=8CM,BC=10CM,求:1.CF 2.EC。
A
B
C
D
E
F
8
10
10
X
8-X
4
8-X
6
1. 几何体的表面路径最短的问题,一般展开表面成平面。
2.利用两点之间线段最短,及勾股定理求解。
专题四 展开思想
规律
例1:如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程 (取3)是( )
A.20cm B.10cm C.14cm D.无法确定
B
B
8
O
A
2
蛋糕
A
C
B
8
周长的一半
6
例2:如图,正方体的棱长为5cm,一只蚂蚁欲从正方体底面上的顶点A沿正方体的表面到顶点C′处吃食物,那么它需要爬行的最短路程的长是多少?
A
B
C
D′
A′
B′
C′
D
例3:如图是一个三级台阶,它的每一级的长宽和高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点最短路程是多少?
20
3
2
A
B
20
2
3
2
3
2
3
A
B
C
∵ AB2=AC2+BC2=625,
∴ AB=25。
例4:如图,长方体的长为15cm,宽为10 cm,高为20cm,点B离点C5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是多少?
10
20
B
A
C
15
5
10
20
B
5
B
5
10
20
A
C
E
F
E
10
20
A
C
F
A
E
C
B
20
15
10
5
1.几何体的内部路径最值的问题,一般画出几何体截面。
2.利用两点之间线段最短及勾股定理求解。
专题五 截面中的勾股定理
规律
小明家住在18层的高楼,一天,他与妈妈去买竹竿。
买最长的吧!
快点回家,好用它凉衣服。
糟糕,太长了,放不进去。
如果电梯的长、宽、高分别是1.5米、1.5米、2.2米,那么,能放入电梯内的竹竿的最大长度大约是多少米?你能估计出小明买的竹竿至少是多少米吗?
1.5米
1.5米
2.2米
1.5米
1.5米
x
x
2.2米
A
B
C
X2=1.52+1.52=4.5
AB2=2.22+X2=9.34
AB≈3米
练习:一种盛饮料的圆柱形杯,测得内部底面半径为2.5㎝,高为12㎝,吸管放进杯里,杯口外面至少要露出4.6㎝,问吸管要做多长?
感悟与反思
1、通过这节课的学习活动你有哪些收获?
2、对这节课的学习,你还有什么想法吗?
谢 谢
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
