北师大版八年级数学上册 3.3 轴对称与坐标变化课件(共32张PPT)
文档属性
| 名称 | 北师大版八年级数学上册 3.3 轴对称与坐标变化课件(共32张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 00:00:00 | ||
图片预览










文档简介
(共32张PPT)
【地位和作用】
1、《变化的鱼》是让学生体会坐标变化和图形变化(如平移、轴对称、伸缩、放大等)之间的内在联系。
2、让学生经历坐标的变化引起图形变化的探索过程,发展学生的形象思维能力和数形结合的意识。
3、培养学生用数学的眼光观察生活,解决生活中出现的问题,对后面学习函数及位似图形起到铺垫作用。
【教学重点和难点】
通过图形坐标变化与图形平移、伸缩、对称之间关系的探索过程,发展学生的形象思维能力和数形结合意识。
探索由坐标的变化引起图形变化的规律。
1、使学生感受在同一直角坐标系中,图形上点的坐标变化与图形变化(平移、对称、伸缩、放大等)之间的关系。
2、通过探索图形坐标变化与图形变化之间的规律,发展学生的形象思维能力和数形结合意识。
【知识和技能目标】
【过程与方法目标】
1、通过学生探究图形的形状、大小、位置变化的过程,掌握空间与图形的基础知识和基本技能。
2、通过图形的平移、对称、伸缩、放大等,培养学生的探索能力。
1、丰富对现实空间及图形的认识,建立初步的空间观念,发展形象思维。
2、通过有趣图形的研究,激发学生对数学学习的好奇心和求知欲,引导学生积极参与数学学习活动。
3、通过《变化的鱼》的学习,让学生体验在数学学习活动中探索与创造的乐趣。
【情感态度与价值观目标】
借助多媒体辅助教学,通过动感的画面,提高学生学习的兴趣,让学生通过画图、观察、猜测、讨论、交流、归纳、总结等数学活动,主动愉快地获取新知识,提高自己解决问题的能力,感受探索与创造的乐趣。
【教学策略】
1、从学生的实际出发,采用“问题情境—探索交流—建立模型—归纳总结—应用拓展”的教学模式安排教学。
2、为了充分调动学生的学习积极性、主动性,使数学课变得生动、有趣,在教学始终贯彻启发、诱导原则,使学生积极参与探究活动,建立模型,总结规律,开阔视野,提高能力。
【教学方法】 导学法、探究法
创设情境
导入新课
探索研究
议一议
做一做
试一试
小结
作业
退出
教师启发诱导
教师点拨
学生自学、互学、讨论思考、交流
开始
创设情境
导入新课
探索研究
议一议
做一做
试一试
小 结
作 业
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
9
10
5
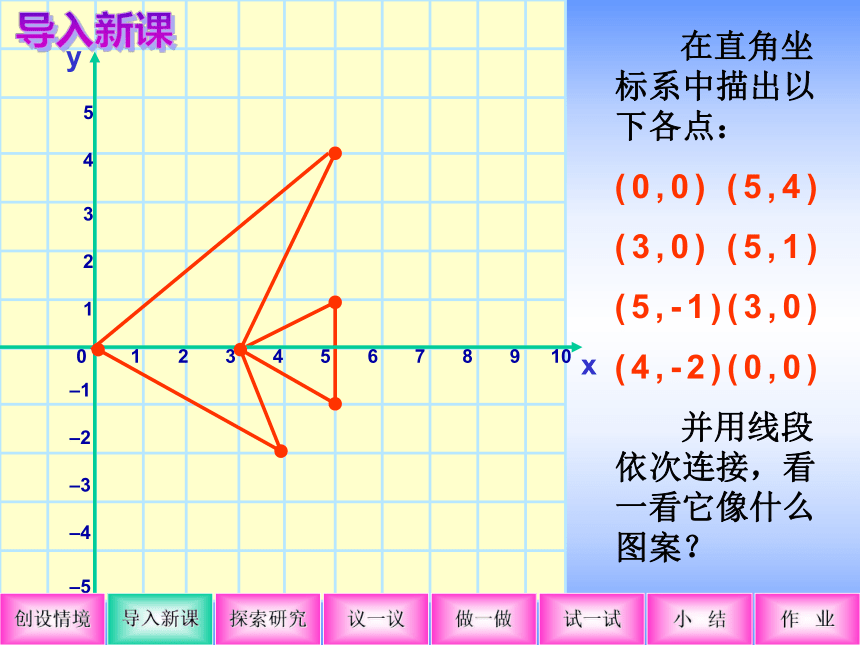
在直角坐标系中描出以下各点:
(0,0) (5,4)
(3,0) (5,1)
(5,-1)(3,0)
(4,-2)(0,0)
并用线段依次连接,看一看它像什么图案?
y
x
创设情境
导入新课
探索研究
议一议
做一做
试一试
小 结
作 业
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
9
10
5
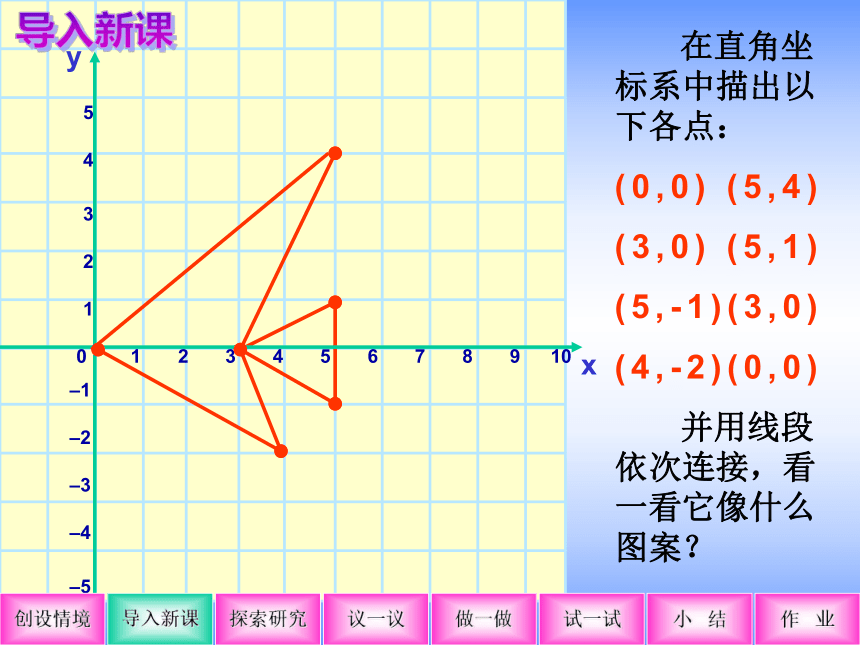
在直角坐标系中描出以下各点:
(0,0) (5,4)
(3,0) (5,1)
(5,-1)(3,0)
(4,-2)(0,0)
并用线段依次连接,看一看它像什么图案?
y
x
创设情境
导入新课
探索研究
议一议
做一做
试一试
小 结
作 业
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
9
10
5
探究一:
图中鱼的坐标为:
(0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)
将左图中的各点做如下变化:
纵坐标保持不变, 横坐标分别加3, 再将所得的图案与原来的图案相比有什么变化?
y
x
原图形向右平移3个单位
探究一
探究二
猜一猜
探究三2
返回
探究三1
考考你
(x,y)→(x+3,y)
探究二:
图中鱼的坐标为:(0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)
将左图中的各点做如下变化:
纵坐标不变, 横坐标分别变为原来的2倍,所得的新图案与原来的图案相比有什么变化?
原图形横向拉伸2倍
探究二
探究一
猜一猜
返回
探究三2
探究三1
考考你
猜一猜
探究二
探究一
返回
探究三2
探究三1
考考你
猜一猜
探究二
探究一
探究三1
横坐标不变,纵坐标分别乘-1,所得图形与原图关于X轴对称。
返回
探究三2
考考你
(x,y)→(x, -y)
探究三:
2、左图中鱼的坐标为:
(0,0) (5,4) (3,0)
(5,1) (5,-1) (3,0)
(4,-2) (0,0)
如果纵、横坐标变成原来的 2倍,所得图案与原图案相比有什么变化
纵、横坐标都乘以2,则图形放大为原来的4倍。
猜一猜
探究二
探究一
探究三2
返回
探究三1
考考你
(x,y)→(2x,2y)
–5
y
x
2
3
4
5
1
0
–1
–2
–3
–4
1
2
3
4
5
–1
–2
–3
–4
–5
1、如果纵坐标不变,横坐标分别乘-1,所得图形与原图相比有什么变化?
2、如果纵、横坐标都乘-1呢?
3、如果纵、横坐标都变为原来的1/2倍呢?
猜一猜
探究二
探究一
考考你
下一页
探究三1
探究三2
–5
y
x
2
3
4
5
1
0
–1
–2
–3
–4
1
2
3
4
5
–1
–2
–3
–4
–5
1、如果纵坐标不变,横坐标分别乘-1,所得图形与原图相比有什么变化?
2、如果纵、横坐标都乘-1呢?
3、如果纵、横坐标都变为原来的1/2倍呢?
猜一猜
探究二
探究一
考考你
下一页
探究三1
探究三2
–5
y
x
2
3
4
5
1
0
–1
–2
–3
–4
1
2
3
4
5
–1
–2
–3
–4
–5
1、如果纵坐标不变,横坐标分别乘-1,所得图形与原图相比有什么变化?
2、如果纵、横坐标都乘-1呢?
3、如果纵、横坐标都变为原来的1/2倍呢?
猜一猜
探究二
探究一
考考你
返回
探究三1
探究三2
3、图形上的点的坐标如何变化,才能使图形上下或左右翻折?
创设情境
导入新课
探索研究
议一议
做一做
试一试
小 结
作 业
1、图形上的点的坐标如何变化,才能使图形上下或左右平移?
2、图形上的点的坐标如何变化,才能使图形上下或左右伸缩?
4、图形上的点的坐标如何变化,才能使图形整体放大或缩小?
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
9
10
5
1、图形上的点的坐标如何变化,才能使图形上下或左右平移?
y
x
议一议1
议一议2
议一议3
议一议4
返回
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
9
10
5
2、图形上的点的坐标如何变化,才能使图形上下或左右伸缩?
y
x
议一议2
议一议1
议一议3
议一议4
返回
–5
y
x
2
3
4
5
1
0
–1
–2
–3
–4
1
2
3
4
5
–1
–2
–3
–4
–5
3、图形上的点的坐标如何变化,才能使图形上下或左右翻折?
议一议3
议一议1
议一议2
议一议4
返回
1
2
3
4
5
6
7
8
0
–2
–4
–6
–8
2
4
6
8
9
10
4、图形上的点的坐标如何变化,才能使图形整体放大或缩小?
y
x
议一议4
议一议1
议一议2
议一议3
返回
1
2
3
4
1
0
4
3
2
–2
–1
–1
–2
–3
–4
–3
–4
将图中的各点纵坐标不变,横坐标乘(-1),与原图相比,所得图案有什么变化?
将图中的各点横坐标不变,纵坐标乘3,与原图相比,所得图案有什么变化?
将图中的各点横坐标不变,纵坐标减3,与原图相比,所得图案有什么变化?
创设情境
导入新课
探索研究
议一议
做一做
试一试
小 结
作 业
1
2
3
4
1
0
y
3
2
–2
–1
–1
–2
–3
–4
–3
1、将图中各个点的坐标乘以-2与原图相比,所得的图案有什么变化。
做一做
试一试
小 结
作 业
–5
–6
5
6
x
创设情境
导入新课
探索研究
议一议
1
2
3
4
5
6
7
8
9
10
x
–4
0
–1
–2
–3
1
2
3
4
5
y
2.“鱼”向下平移2个单位,再向右平移4个单位,坐标会有什么样的变化?
3.试用这节课所学到的知识解决创设情境中出现的问题。
做一做
试一试
小 结
作 业
创设情境
导入新课
探索研究
议一议
1
2
3
4
5
6
7
8
9
10
x
–4
0
–1
–2
–3
1
2
3
4
5
y
2.“鱼”向下平移2个单位,再向右平移4个单位,坐标会有什么样的变化?
3.试用这节课所学到的知识解决创设情境中出现的问题。
做一做
试一试
小 结
作 业
创设情境
导入新课
探索研究
议一议
本节课主要研究横坐标或纵坐标发生有序变化时,新、旧图形相比有什么变化,找出规律。
试一试
小 结
作 业
做一做
创设情境
导入新课
探索研究
议一议
图形的坐标变化与图形变换之间的规律:
一、图形的平移
二、图形的伸缩
三、图形的对称
四、图形的放大(缩小)
做一做
试一试
1、通过创设情境,引起学生的好奇心,激发学生兴趣。新知识都是通过学生自主探索、合作学习所获得,这与新课标的教学理念相辅相成。从学生的参与程度,练习的反馈等情况来看,实现了本节课预定的教学目标。
2、在教学策略上,教师并不是将新知识和盘托出交给学生,而是通过引导学生对新旧图形的变化进行观察、交流、讨论、思考等,建立模型进而归纳出规律,促使学生主动参与知识的形成过程,既符合学生学习的认知规律,又突出了学生的主体地位。
3、注重学生的形象思维能力和数形结合意识的培养。关注同学们在学习过程中表现出来的与人合作态度,表达与交流的意识和探索的精神。
【地位和作用】
1、《变化的鱼》是让学生体会坐标变化和图形变化(如平移、轴对称、伸缩、放大等)之间的内在联系。
2、让学生经历坐标的变化引起图形变化的探索过程,发展学生的形象思维能力和数形结合的意识。
3、培养学生用数学的眼光观察生活,解决生活中出现的问题,对后面学习函数及位似图形起到铺垫作用。
【教学重点和难点】
通过图形坐标变化与图形平移、伸缩、对称之间关系的探索过程,发展学生的形象思维能力和数形结合意识。
探索由坐标的变化引起图形变化的规律。
1、使学生感受在同一直角坐标系中,图形上点的坐标变化与图形变化(平移、对称、伸缩、放大等)之间的关系。
2、通过探索图形坐标变化与图形变化之间的规律,发展学生的形象思维能力和数形结合意识。
【知识和技能目标】
【过程与方法目标】
1、通过学生探究图形的形状、大小、位置变化的过程,掌握空间与图形的基础知识和基本技能。
2、通过图形的平移、对称、伸缩、放大等,培养学生的探索能力。
1、丰富对现实空间及图形的认识,建立初步的空间观念,发展形象思维。
2、通过有趣图形的研究,激发学生对数学学习的好奇心和求知欲,引导学生积极参与数学学习活动。
3、通过《变化的鱼》的学习,让学生体验在数学学习活动中探索与创造的乐趣。
【情感态度与价值观目标】
借助多媒体辅助教学,通过动感的画面,提高学生学习的兴趣,让学生通过画图、观察、猜测、讨论、交流、归纳、总结等数学活动,主动愉快地获取新知识,提高自己解决问题的能力,感受探索与创造的乐趣。
【教学策略】
1、从学生的实际出发,采用“问题情境—探索交流—建立模型—归纳总结—应用拓展”的教学模式安排教学。
2、为了充分调动学生的学习积极性、主动性,使数学课变得生动、有趣,在教学始终贯彻启发、诱导原则,使学生积极参与探究活动,建立模型,总结规律,开阔视野,提高能力。
【教学方法】 导学法、探究法
创设情境
导入新课
探索研究
议一议
做一做
试一试
小结
作业
退出
教师启发诱导
教师点拨
学生自学、互学、讨论思考、交流
开始
创设情境
导入新课
探索研究
议一议
做一做
试一试
小 结
作 业
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
9
10
5
在直角坐标系中描出以下各点:
(0,0) (5,4)
(3,0) (5,1)
(5,-1)(3,0)
(4,-2)(0,0)
并用线段依次连接,看一看它像什么图案?
y
x
创设情境
导入新课
探索研究
议一议
做一做
试一试
小 结
作 业
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
9
10
5
在直角坐标系中描出以下各点:
(0,0) (5,4)
(3,0) (5,1)
(5,-1)(3,0)
(4,-2)(0,0)
并用线段依次连接,看一看它像什么图案?
y
x
创设情境
导入新课
探索研究
议一议
做一做
试一试
小 结
作 业
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
9
10
5
探究一:
图中鱼的坐标为:
(0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)
将左图中的各点做如下变化:
纵坐标保持不变, 横坐标分别加3, 再将所得的图案与原来的图案相比有什么变化?
y
x
原图形向右平移3个单位
探究一
探究二
猜一猜
探究三2
返回
探究三1
考考你
(x,y)→(x+3,y)
探究二:
图中鱼的坐标为:(0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)
将左图中的各点做如下变化:
纵坐标不变, 横坐标分别变为原来的2倍,所得的新图案与原来的图案相比有什么变化?
原图形横向拉伸2倍
探究二
探究一
猜一猜
返回
探究三2
探究三1
考考你
猜一猜
探究二
探究一
返回
探究三2
探究三1
考考你
猜一猜
探究二
探究一
探究三1
横坐标不变,纵坐标分别乘-1,所得图形与原图关于X轴对称。
返回
探究三2
考考你
(x,y)→(x, -y)
探究三:
2、左图中鱼的坐标为:
(0,0) (5,4) (3,0)
(5,1) (5,-1) (3,0)
(4,-2) (0,0)
如果纵、横坐标变成原来的 2倍,所得图案与原图案相比有什么变化
纵、横坐标都乘以2,则图形放大为原来的4倍。
猜一猜
探究二
探究一
探究三2
返回
探究三1
考考你
(x,y)→(2x,2y)
–5
y
x
2
3
4
5
1
0
–1
–2
–3
–4
1
2
3
4
5
–1
–2
–3
–4
–5
1、如果纵坐标不变,横坐标分别乘-1,所得图形与原图相比有什么变化?
2、如果纵、横坐标都乘-1呢?
3、如果纵、横坐标都变为原来的1/2倍呢?
猜一猜
探究二
探究一
考考你
下一页
探究三1
探究三2
–5
y
x
2
3
4
5
1
0
–1
–2
–3
–4
1
2
3
4
5
–1
–2
–3
–4
–5
1、如果纵坐标不变,横坐标分别乘-1,所得图形与原图相比有什么变化?
2、如果纵、横坐标都乘-1呢?
3、如果纵、横坐标都变为原来的1/2倍呢?
猜一猜
探究二
探究一
考考你
下一页
探究三1
探究三2
–5
y
x
2
3
4
5
1
0
–1
–2
–3
–4
1
2
3
4
5
–1
–2
–3
–4
–5
1、如果纵坐标不变,横坐标分别乘-1,所得图形与原图相比有什么变化?
2、如果纵、横坐标都乘-1呢?
3、如果纵、横坐标都变为原来的1/2倍呢?
猜一猜
探究二
探究一
考考你
返回
探究三1
探究三2
3、图形上的点的坐标如何变化,才能使图形上下或左右翻折?
创设情境
导入新课
探索研究
议一议
做一做
试一试
小 结
作 业
1、图形上的点的坐标如何变化,才能使图形上下或左右平移?
2、图形上的点的坐标如何变化,才能使图形上下或左右伸缩?
4、图形上的点的坐标如何变化,才能使图形整体放大或缩小?
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
9
10
5
1、图形上的点的坐标如何变化,才能使图形上下或左右平移?
y
x
议一议1
议一议2
议一议3
议一议4
返回
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
9
10
5
2、图形上的点的坐标如何变化,才能使图形上下或左右伸缩?
y
x
议一议2
议一议1
议一议3
议一议4
返回
–5
y
x
2
3
4
5
1
0
–1
–2
–3
–4
1
2
3
4
5
–1
–2
–3
–4
–5
3、图形上的点的坐标如何变化,才能使图形上下或左右翻折?
议一议3
议一议1
议一议2
议一议4
返回
1
2
3
4
5
6
7
8
0
–2
–4
–6
–8
2
4
6
8
9
10
4、图形上的点的坐标如何变化,才能使图形整体放大或缩小?
y
x
议一议4
议一议1
议一议2
议一议3
返回
1
2
3
4
1
0
4
3
2
–2
–1
–1
–2
–3
–4
–3
–4
将图中的各点纵坐标不变,横坐标乘(-1),与原图相比,所得图案有什么变化?
将图中的各点横坐标不变,纵坐标乘3,与原图相比,所得图案有什么变化?
将图中的各点横坐标不变,纵坐标减3,与原图相比,所得图案有什么变化?
创设情境
导入新课
探索研究
议一议
做一做
试一试
小 结
作 业
1
2
3
4
1
0
y
3
2
–2
–1
–1
–2
–3
–4
–3
1、将图中各个点的坐标乘以-2与原图相比,所得的图案有什么变化。
做一做
试一试
小 结
作 业
–5
–6
5
6
x
创设情境
导入新课
探索研究
议一议
1
2
3
4
5
6
7
8
9
10
x
–4
0
–1
–2
–3
1
2
3
4
5
y
2.“鱼”向下平移2个单位,再向右平移4个单位,坐标会有什么样的变化?
3.试用这节课所学到的知识解决创设情境中出现的问题。
做一做
试一试
小 结
作 业
创设情境
导入新课
探索研究
议一议
1
2
3
4
5
6
7
8
9
10
x
–4
0
–1
–2
–3
1
2
3
4
5
y
2.“鱼”向下平移2个单位,再向右平移4个单位,坐标会有什么样的变化?
3.试用这节课所学到的知识解决创设情境中出现的问题。
做一做
试一试
小 结
作 业
创设情境
导入新课
探索研究
议一议
本节课主要研究横坐标或纵坐标发生有序变化时,新、旧图形相比有什么变化,找出规律。
试一试
小 结
作 业
做一做
创设情境
导入新课
探索研究
议一议
图形的坐标变化与图形变换之间的规律:
一、图形的平移
二、图形的伸缩
三、图形的对称
四、图形的放大(缩小)
做一做
试一试
1、通过创设情境,引起学生的好奇心,激发学生兴趣。新知识都是通过学生自主探索、合作学习所获得,这与新课标的教学理念相辅相成。从学生的参与程度,练习的反馈等情况来看,实现了本节课预定的教学目标。
2、在教学策略上,教师并不是将新知识和盘托出交给学生,而是通过引导学生对新旧图形的变化进行观察、交流、讨论、思考等,建立模型进而归纳出规律,促使学生主动参与知识的形成过程,既符合学生学习的认知规律,又突出了学生的主体地位。
3、注重学生的形象思维能力和数形结合意识的培养。关注同学们在学习过程中表现出来的与人合作态度,表达与交流的意识和探索的精神。
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
