人教版九年级上册数学 22.4弧长和扇形的面积--求图形旋转后扫过的面积训练(word版含答案)
文档属性
| 名称 | 人教版九年级上册数学 22.4弧长和扇形的面积--求图形旋转后扫过的面积训练(word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 409.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 21:19:54 | ||
图片预览



文档简介
人教版九年级上册数学22.4弧长和扇形的面积--求图形旋转后扫过的面积训练
一、单选题
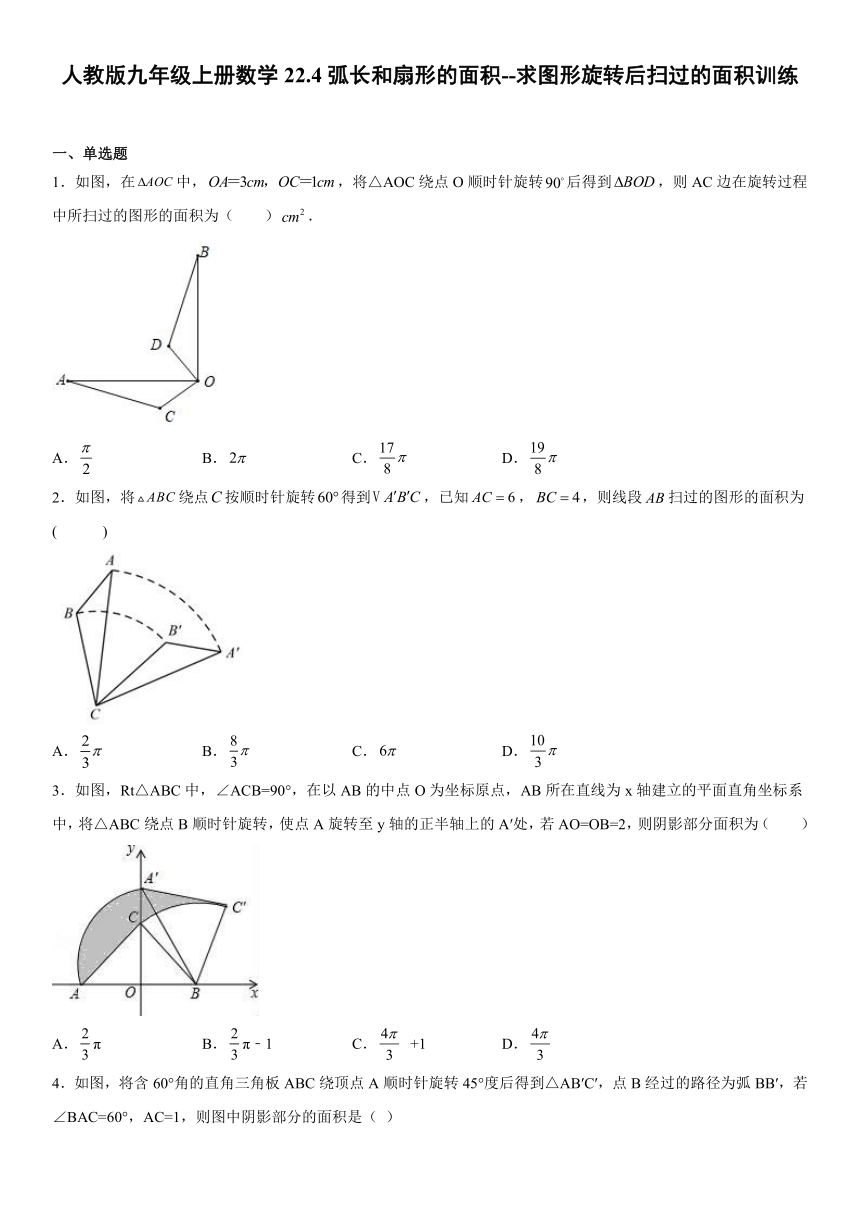
1.如图,在中,,将△AOC绕点O顺时针旋转后得到,则AC边在旋转过程中所扫过的图形的面积为( ).
A. B. C. D.
2.如图,将绕点按顺时针旋转得到,已知,,则线段扫过的图形的面积为( )
A. B. C. D.
3.如图,Rt△ABC中,∠ACB=90°,在以AB的中点O为坐标原点,AB所在直线为x轴建立的平面直角坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴的正半轴上的A′处,若AO=OB=2,则阴影部分面积为( )
A.π B.π﹣1 C. +1 D.
4.如图,将含60°角的直角三角板ABC绕顶点A顺时针旋转45°度后得到△AB′C′,点B经过的路径为弧BB′,若∠BAC=60°,AC=1,则图中阴影部分的面积是( )
A. B. C. D.π
5.如图,某数学兴趣小组将边长为6的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形DAB的面积为( )
A.12 B.14 C.16 D.36
6.如图,在中,.将绕点按顺时针方向旋转度后得到,此时点在边上,斜边交边于点,则的大小和图中阴影部分的面积分别为( )
A. B.
C. D.
二、填空题
7.已知线段AB=2,以点A 为旋转中心,如果将AB顺时针旋转120°,那么线段AB所扫过的图形的面积为__________(答案保留)
8.如图,Rt△ABC中,∠B=90°, AB = 6,BC = 8,且,将Rt△ABC绕点C按顺时针方向旋转90°,得到Rt△A’B’C,则边AB扫过的面积(图中阴影部分)是____________.
9.如图,Rt△ABC中,∠ACB=90°,∠A=30°,BC=6,D,E分别是AB,AC边的中点,将△ABC绕点B顺时针旋转60°到△A′BC′的位置,则整个旋转过程中线段DE所扫过部分的面积(即图中阴影部分面积)为_____.
10.如图,将三角形AOC绕点O顺时针旋转120°得三角形BOD,已知OA=4,OC=1,那么图中阴影部分的面积为_____.(结果保留π)
11.如图,已知A(2,2),B(2,1),将△AOB绕着点O逆时针旋转,使点A旋转到点A′(-2,2)的位置,则图中阴影部分的面积为________.
12.如图,C为半圆内一点,O为圆心,直径AB长为2 cm,∠BOC=60°,∠BCO=90°,将△BOC绕圆心O逆时针旋转至△B′OC′,点C′在OA上,则边BC扫过区域(图中阴影部分)的面积为_________cm2.
13.如图,Rt△ABC中,∠ACB=90°,∠CAB=30°,BC=2,点O、H分别为边AB、AC的中点,将△ABC绕点B顺时针旋转120°到△A1BC1的位置,则整个旋转过程中线段OH所扫过部分的面积(即阴影部分面积)为______.
三、解答题
14.如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
(1)在正方形网格中,画出△AB′C′;
(2)计算线段AB在变换到AB′的过程中扫过区域的面积.
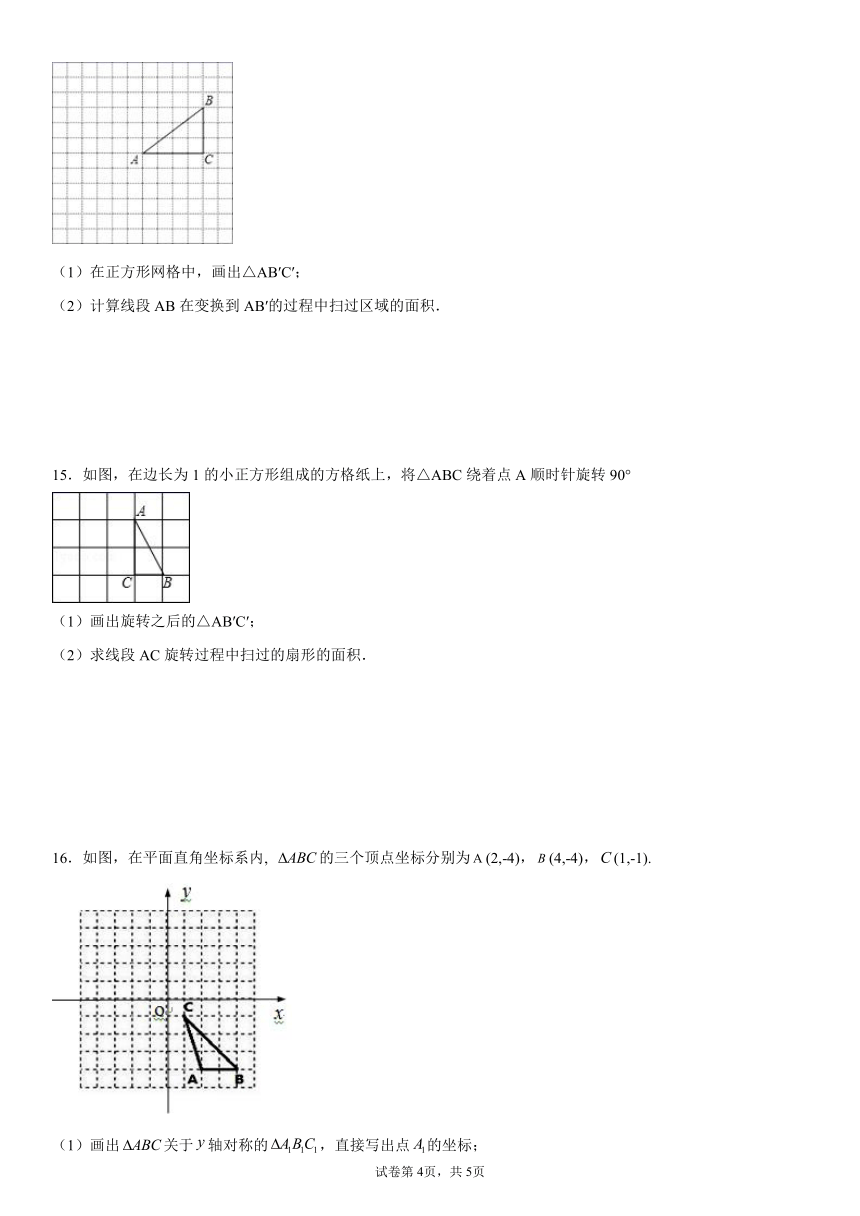
15.如图,在边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90°
(1)画出旋转之后的△AB′C′;
(2)求线段AC旋转过程中扫过的扇形的面积.
16.如图,在平面直角坐标系内, 的三个顶点坐标分别为(2,-4),(4,-4),(1,-1).
(1)画出关于轴对称的,直接写出点的坐标;
(2)画出绕点逆时针旋转90°后的;
(3)在(2)的条件下,求线段扫过的面积(结果保留π).
17.如图,直角坐标系中,Rt△DOC的直角边OC在x轴上,∠OCD=90°,OD=6,OC=3,现将△DOC绕原点O按逆时针方向旋转,得到△AOB,且点A在x轴上.
(1)请直接写出:∠A的度数.
(2)请求出线段OD扫过的面积.
18.已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(﹣1,2)、B(﹣2,1)、C(1,1)(正方形网格中每个小正方形的边长是1个单位长度).
(1)△A1B1C1是△ABC绕点__逆时针旋转__度得到的,B1的坐标是__;
(2)求出线段AC旋转过程中所扫过的面积(结果保留π).
参考答案
1.B
2.D
3.D
4.A
5.D
6.C
7.
8.9π
9..
10.5π
11.
12.
13.π
14.
(1)解:如图所示:△AB′C′即为所求
(2)解:∵AB= =5,
∴线段AB在变换到AB′的过程中扫过区域的面积为:=π
15.
解:(1)△AB′C′如图所示:
(2)由图可知,AC=2,
∴线段AC旋转过程中扫过的扇形的面积.
16.
试题分析:(1)由题意画出即可;关于y轴对称点的坐标纵坐标不变,横坐标互为相反数;
(2)由网格结构找出点A、B、C以点O为旋转中心顺时针旋转90°后的对应点,然后顺次连接即可;
(3)利用△ABC旋转时BC线段扫过的面积S扇形BOB2﹣S扇形COC2即可求出.
试题解析:解:(1)如图所示,A1坐标为(﹣2,﹣4),故答案为(﹣2,﹣4);
(2)如图所示;
(3)∵OC=,OB=,∴△ABC旋转时BC线段扫过的面积
S扇形BOB2﹣S扇形COC2=﹣==.
17.
(1)=30°; 3分
(2)在Rt△DOC,∠OCD=90°,OD=6,OC=3,
∴, 5分
∴=60°,
∴=180°-60°=120°, 7分
∴线段OD扫过的面积为.9分
18.
解:(1)△A1B1C1是△ABC绕点C逆时针旋转90度得到的,
B1的坐标是:(1,﹣2),
故答案为:C,90,(1,﹣2);
(2)线段AC旋转过程中所扫过的面积为以点C为圆心,AC为半径的扇形的面积.
∵AC==,
∴面积为:=,
即线段AC旋转过程中所扫过的面积为.
试卷第4页,共5页
一、单选题
1.如图,在中,,将△AOC绕点O顺时针旋转后得到,则AC边在旋转过程中所扫过的图形的面积为( ).
A. B. C. D.
2.如图,将绕点按顺时针旋转得到,已知,,则线段扫过的图形的面积为( )
A. B. C. D.
3.如图,Rt△ABC中,∠ACB=90°,在以AB的中点O为坐标原点,AB所在直线为x轴建立的平面直角坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴的正半轴上的A′处,若AO=OB=2,则阴影部分面积为( )
A.π B.π﹣1 C. +1 D.
4.如图,将含60°角的直角三角板ABC绕顶点A顺时针旋转45°度后得到△AB′C′,点B经过的路径为弧BB′,若∠BAC=60°,AC=1,则图中阴影部分的面积是( )
A. B. C. D.π
5.如图,某数学兴趣小组将边长为6的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得的扇形DAB的面积为( )
A.12 B.14 C.16 D.36
6.如图,在中,.将绕点按顺时针方向旋转度后得到,此时点在边上,斜边交边于点,则的大小和图中阴影部分的面积分别为( )
A. B.
C. D.
二、填空题
7.已知线段AB=2,以点A 为旋转中心,如果将AB顺时针旋转120°,那么线段AB所扫过的图形的面积为__________(答案保留)
8.如图,Rt△ABC中,∠B=90°, AB = 6,BC = 8,且,将Rt△ABC绕点C按顺时针方向旋转90°,得到Rt△A’B’C,则边AB扫过的面积(图中阴影部分)是____________.
9.如图,Rt△ABC中,∠ACB=90°,∠A=30°,BC=6,D,E分别是AB,AC边的中点,将△ABC绕点B顺时针旋转60°到△A′BC′的位置,则整个旋转过程中线段DE所扫过部分的面积(即图中阴影部分面积)为_____.
10.如图,将三角形AOC绕点O顺时针旋转120°得三角形BOD,已知OA=4,OC=1,那么图中阴影部分的面积为_____.(结果保留π)
11.如图,已知A(2,2),B(2,1),将△AOB绕着点O逆时针旋转,使点A旋转到点A′(-2,2)的位置,则图中阴影部分的面积为________.
12.如图,C为半圆内一点,O为圆心,直径AB长为2 cm,∠BOC=60°,∠BCO=90°,将△BOC绕圆心O逆时针旋转至△B′OC′,点C′在OA上,则边BC扫过区域(图中阴影部分)的面积为_________cm2.
13.如图,Rt△ABC中,∠ACB=90°,∠CAB=30°,BC=2,点O、H分别为边AB、AC的中点,将△ABC绕点B顺时针旋转120°到△A1BC1的位置,则整个旋转过程中线段OH所扫过部分的面积(即阴影部分面积)为______.
三、解答题
14.如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
(1)在正方形网格中,画出△AB′C′;
(2)计算线段AB在变换到AB′的过程中扫过区域的面积.
15.如图,在边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转90°
(1)画出旋转之后的△AB′C′;
(2)求线段AC旋转过程中扫过的扇形的面积.
16.如图,在平面直角坐标系内, 的三个顶点坐标分别为(2,-4),(4,-4),(1,-1).
(1)画出关于轴对称的,直接写出点的坐标;
(2)画出绕点逆时针旋转90°后的;
(3)在(2)的条件下,求线段扫过的面积(结果保留π).
17.如图,直角坐标系中,Rt△DOC的直角边OC在x轴上,∠OCD=90°,OD=6,OC=3,现将△DOC绕原点O按逆时针方向旋转,得到△AOB,且点A在x轴上.
(1)请直接写出:∠A的度数.
(2)请求出线段OD扫过的面积.
18.已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(﹣1,2)、B(﹣2,1)、C(1,1)(正方形网格中每个小正方形的边长是1个单位长度).
(1)△A1B1C1是△ABC绕点__逆时针旋转__度得到的,B1的坐标是__;
(2)求出线段AC旋转过程中所扫过的面积(结果保留π).
参考答案
1.B
2.D
3.D
4.A
5.D
6.C
7.
8.9π
9..
10.5π
11.
12.
13.π
14.
(1)解:如图所示:△AB′C′即为所求
(2)解:∵AB= =5,
∴线段AB在变换到AB′的过程中扫过区域的面积为:=π
15.
解:(1)△AB′C′如图所示:
(2)由图可知,AC=2,
∴线段AC旋转过程中扫过的扇形的面积.
16.
试题分析:(1)由题意画出即可;关于y轴对称点的坐标纵坐标不变,横坐标互为相反数;
(2)由网格结构找出点A、B、C以点O为旋转中心顺时针旋转90°后的对应点,然后顺次连接即可;
(3)利用△ABC旋转时BC线段扫过的面积S扇形BOB2﹣S扇形COC2即可求出.
试题解析:解:(1)如图所示,A1坐标为(﹣2,﹣4),故答案为(﹣2,﹣4);
(2)如图所示;
(3)∵OC=,OB=,∴△ABC旋转时BC线段扫过的面积
S扇形BOB2﹣S扇形COC2=﹣==.
17.
(1)=30°; 3分
(2)在Rt△DOC,∠OCD=90°,OD=6,OC=3,
∴, 5分
∴=60°,
∴=180°-60°=120°, 7分
∴线段OD扫过的面积为.9分
18.
解:(1)△A1B1C1是△ABC绕点C逆时针旋转90度得到的,
B1的坐标是:(1,﹣2),
故答案为:C,90,(1,﹣2);
(2)线段AC旋转过程中所扫过的面积为以点C为圆心,AC为半径的扇形的面积.
∵AC==,
∴面积为:=,
即线段AC旋转过程中所扫过的面积为.
试卷第4页,共5页
同课章节目录
