北师大版八年级数学下册 第六章平行四边形 复习课件(共38张PPT)
文档属性
| 名称 | 北师大版八年级数学下册 第六章平行四边形 复习课件(共38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 463.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 21:04:18 | ||
图片预览



文档简介
(共38张PPT)
第六章 平行四边形 复习课件
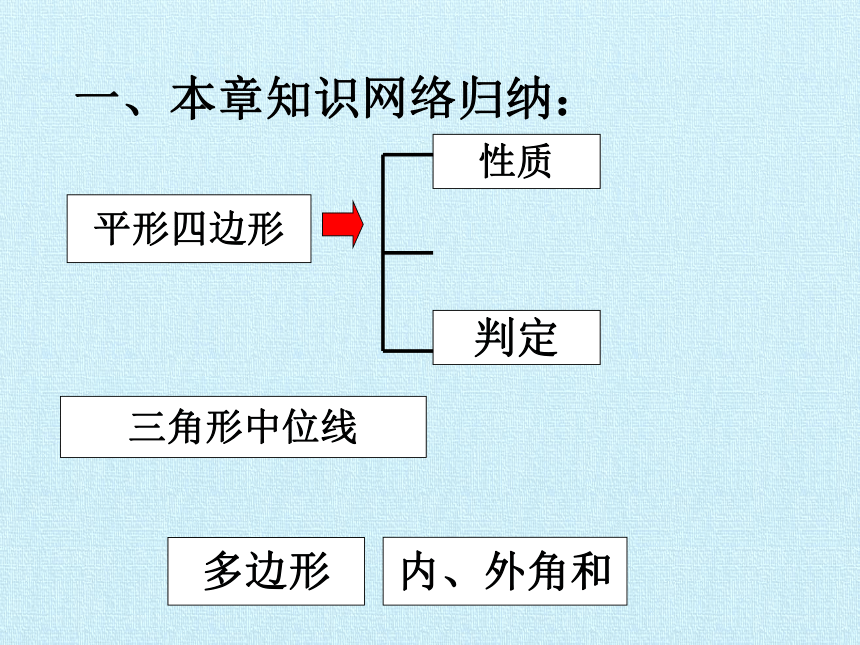
一、本章知识网络归纳:
多边形
内、外角和
平形四边形
三角形中位线
性质
判定
二、平行四边形的性质有:
平行四边形的对边相等。
平行四边形的对边平行。
平行四边形的对角相等。
平行四边形的对角线互相平分。
数学语言:∵在 ABCD中,∴AB=CD,AD=BC
数学语言:∵在 ABCD中,∴AB∥CD,AD∥BC
数学语言:∵在 ABCD中,∴∠B=∠D,∠A=∠C
数学语言:∵在 ABCD中,∴OB=OD,OA=OC
O
A
B
D
C
O
A
B
D
C
O
如图,把两张完全相同的平行四边形纸片叠合在一起,在它们的中心O钉一个图钉,将一个平行四边形绕O旋转180°,你发现了什么?
●
A
D
O
C
B
D
B
O
C
A
再看一遍
看一看
●
A
D
O
C
B
D
B
O
C
A
看一看
平行四边形是中心对称图形,但不是轴对称图形。
1、如图,四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,求BC、CD、AC、OA的长以及 ABCD的面积。
8
10
B
C
D
A
●
O
解:
∴△ABC是直角三角形
又∵AC⊥BC
∵四边形ABCD是平行四边形
∴BC=AD=8,CD=AB=10
又∵OA=OC
∴
∴
∴S =BC×AC=8×6=48
ABCD
基本练习
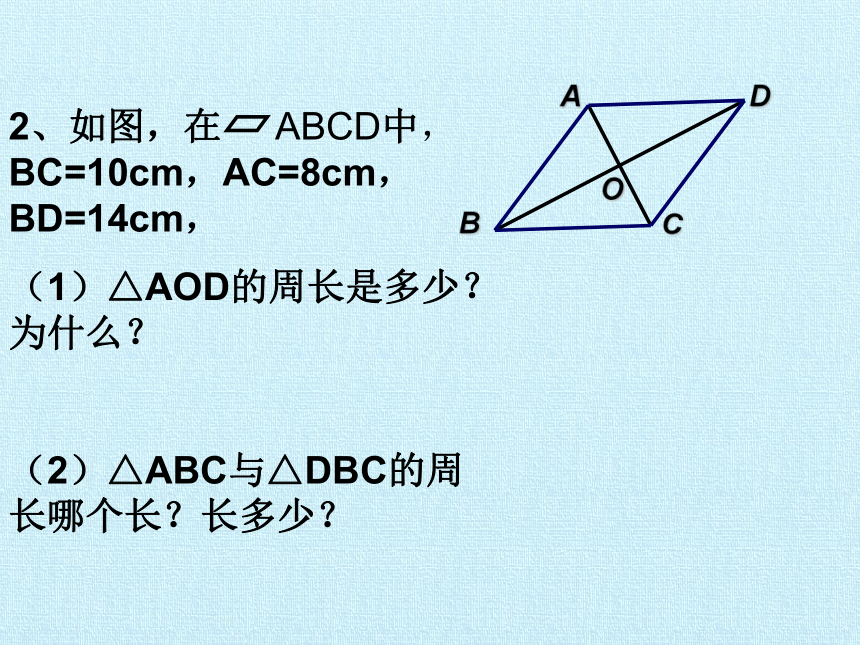
2、如图,在 ABCD中,BC=10cm,AC=8cm,BD=14cm,
(1)△AOD的周长是多少?为什么?
(2)△ABC与△DBC的周长哪个长?长多少?
A
B
D
C
O
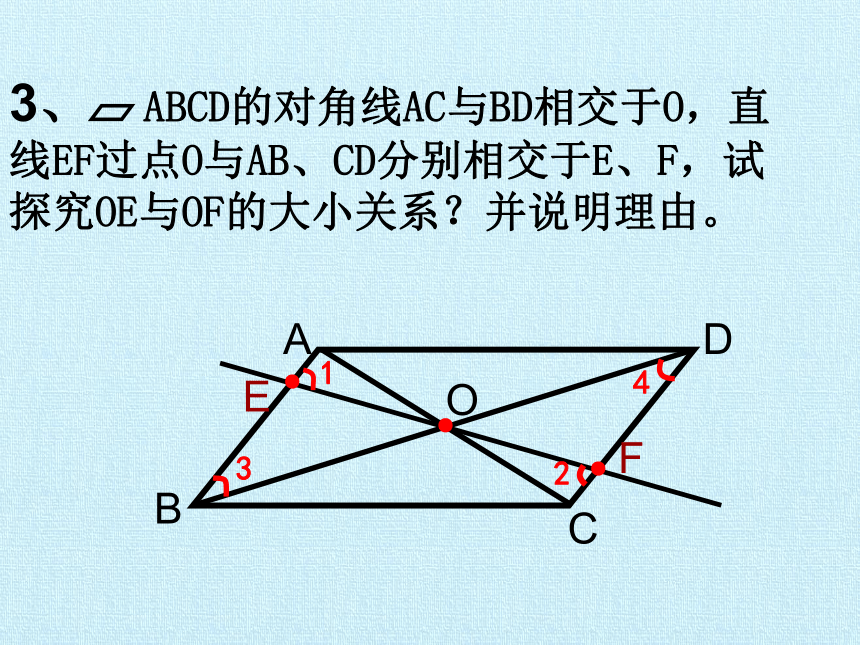
3、 ABCD的对角线AC与BD相交于O,直线EF过点O与AB、CD分别相交于E、F,试探究OE与OF的大小关系?并说明理由。
A
B
C
D
O
E
F
●
●
●
1
2
3
4
●
O
D
C
B
A
E
F
●
O
D
C
B
A
E
F
(1)
(2)
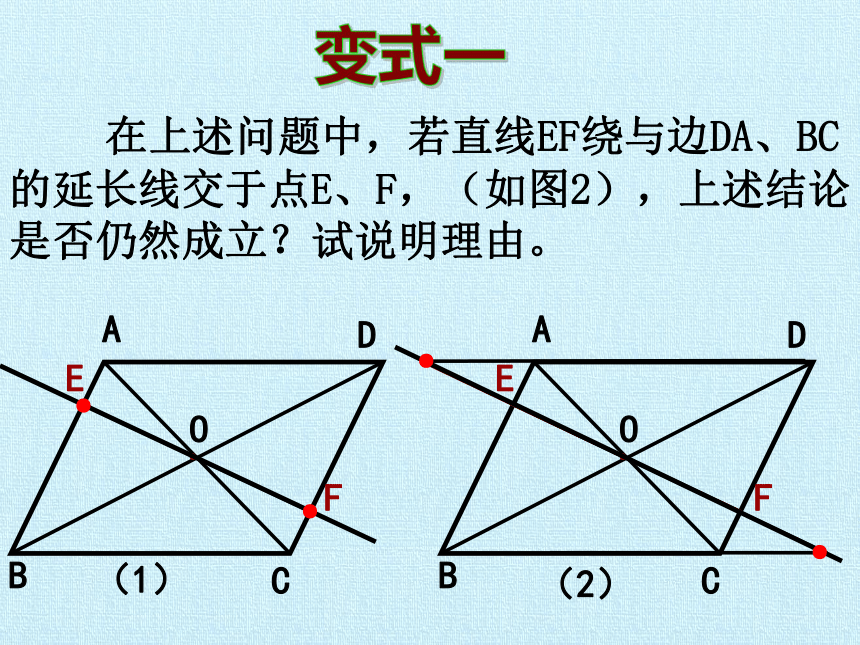
在上述问题中,若直线EF绕与边DA、BC的延长线交于点E、F,(如图2),上述结论是否仍然成立?试说明理由。
变式一
●
●
●
●
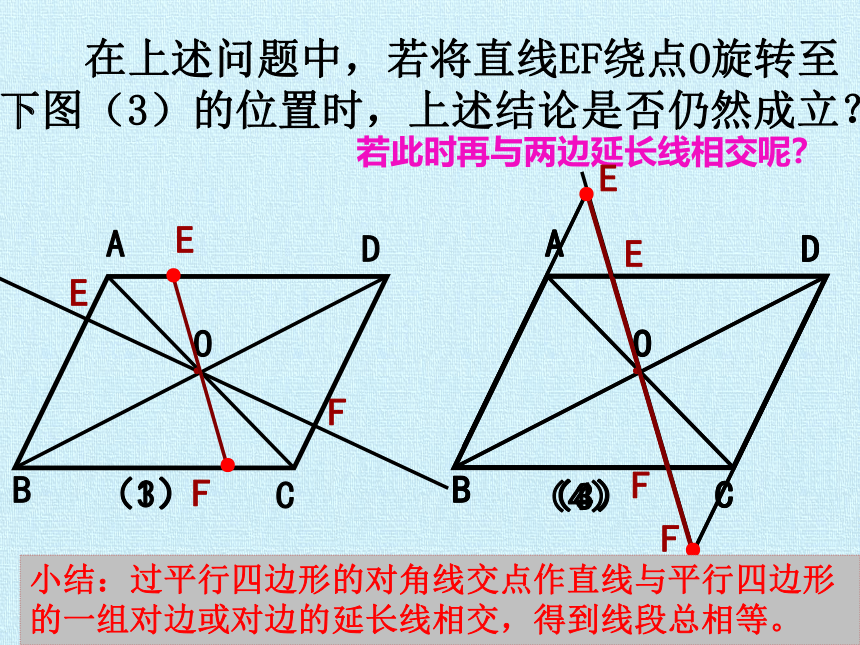
在上述问题中,若将直线EF绕点O旋转至下图(3)的位置时,上述结论是否仍然成立?
F
E
F
●
O
D
C
B
A
E
(1)
●
O
D
C
B
A
E
F
(3)
(3)
(4)
若此时再与两边延长线相交呢?
●
O
D
C
B
A
E
F
(4)
●
●
●
●
变式二
小结:过平行四边形的对角线交点作直线与平行四边形的一组对边或对边的延长线相交,得到线段总相等。
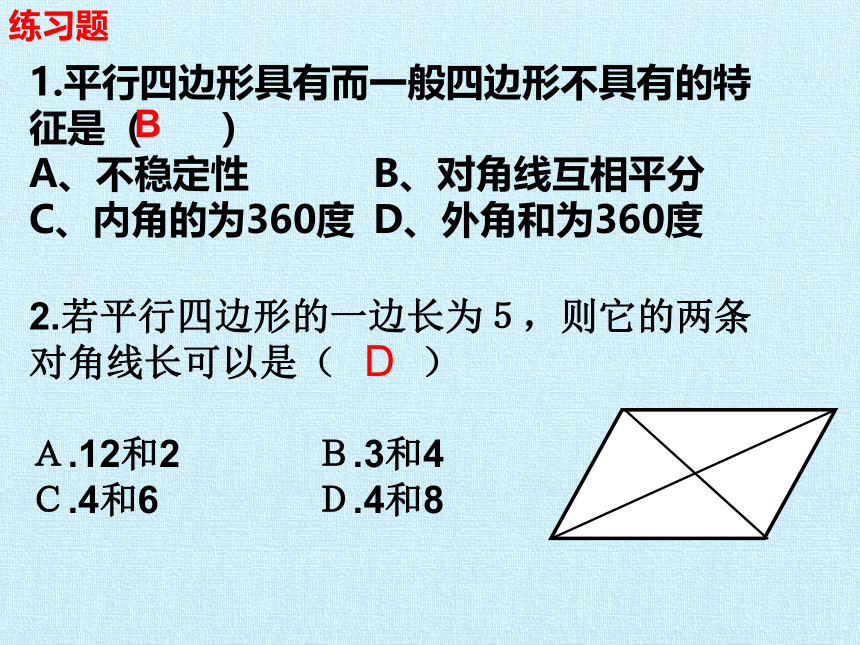
1.平行四边形具有而一般四边形不具有的特征是( )
A、不稳定性 B、对角线互相平分
C、内角的为360度 D、外角和为360度
B
练习题
2.若平行四边形的一边长为5,则它的两条对角线长可以是( )
A.12和2 B.3和4
C.4和6 D.4和8
D
3.如图,在平面直角坐标系中, OBCD的顶点
O、B、D的坐标如图所示,则顶点C的坐标为( )
x
Y
C
O (0,0)
B(5,0)
D(2,3)
A.(3,7) B.(5,3)
C.(7,3) D.(8,2)
C
4.如图,在 ABCD中,对角线AC,BD交于点O,AC=10,BD=8,则AD的取值范围是_________。
O
D
B
A
C
●
1<AD<9
O
D
B
A
C
5.如图,在 ABCD中,对角线AC、BD相交于点O,且AC+BD=20,△AOB的周长等于15,
则CD=______。
5
一位饱经苍桑的老人,经过一辈子的辛勤劳动,到晚年的时候,终于拥有了一块平行四边形的土地,由于年迈体弱,他决定把这块土地分给他的四个孩子,他是这样分的:
老大
老二
老三
老四
当四个孩子看到时,争论不休,都认为自己的地少,同学们,你认为老人这样分合理吗?为什么?
A
B
D
O
E
F
A
B
C
D
O
E
F
A
B
C
D
O
E
F
C
A
B
C
D
O
E
F
在这些图形中面积相等的图形有哪些?
过对角线交点的任一条直线都将平行四边形分成面积相等的两部分。
拓展
定理2:两组对边分别相等的四边形是平行四边形。
定义:两组对边分别平行的四边形是平行四边形。
定理1:一组对边平行且相等的四边形平行四边形。
三、平行四边形的判定:
定理3:对角线互相平分的四边形是平行四边形。
定理4:两组对角分别相等的四边形是平行四边形。(补充)
数学语言:∵AB∥CD,AD∥BC。∴四边形ABCD是平行四边形。
数学语言:∵AB∥CD,AB=CD。∴四边形ABCD是平行四边形。
数学语言:∵AB=CD,AD=BC。∴四边形ABCD是平行四边形。
数学语言:∵AO=CO,OD=BO。∴四边形ABCD是平行四边形。
从边来判定
1、两组对边分别平行的四边形是平行四边形
2、两组对边分别相等的四边形是平行四边形
3、一组对边平行且相等的四边形是平行四边形
从角来判定
两组对角分别相等的四边形是平行四边形
从对角线来判定
两条对角线互相平分的四边形是平行四边形
理一理
平行四边形的判定方法
1、如图,已知AC是□ABCD的一条对角线,BM⊥AC
于M,DN⊥AC于N,求证:四边形BMDN是平行四边形。
证明:连接BD交AC于O。
∵BM⊥AC于M,DN⊥AC于N,
∴∠AND=∠CMB=90°。
∵四边形ABCD是平行四边形,
∴OB=OD,OA=OC,AD CB。
∴∠DAN=∠BCM
∴△ADN≌△CBM
∴AN=CM。
∴OA-AN=OC-CM,
即ON=OM
∴四边形BMDN是平行四边形。
∥
=
2、在四边形ABCD中,对角线AC、BD交于O点,且OA=OC,OB=OD,△AOD的周长比△AOB的周长4cm,AD:AB=2:1,求四边形ABCD的周长。
解:∵OA=OC,OB=OD
∴ABCD是平行四边形
△AOD的周长=AD+OA+OD
△AOB的周长=AB+OA+OB
△AOD的周长比△AOB的周长多4cm,
即(AD+OA+OD)-(AB+OA+OB)=4cm
化简得AD-AB=4cm,又因为AD:AB=2:1
∴AD=8cm,AB=4cm
平行四边形ABCD周长=(8+4)×2=24cm
O
D
C
B
A
1、已知:如图,在平行四边形ABCD中,E,F分别是
AB,DC上的两点,且AE=CF。
求证:BD,EF互相平分。
快速解答:
2、已知:如图,在平行四边形ABCD中,点M,N在对角线AC上,且AM=CN。
求证:四边形BMDN是平行四边形。
3、已知:如图,在平行四边形ABCD中,E,F分别是AB,CD上的两点,且AE=CF,AF,DE相交于点M,BF,CE相交于点N。
求证:四边形EMFN是平行四边形。
N
M
B
A
C
D
E
F
三角形的中位线平行于第三边,并且等于第三边的一半。
四、三角形的中位线
A
B
C
D
E
数学语言:∵DE是△ABC的中位线∴DE= ,DE∥BC。
1、三角形各边的长分别为6cm、8cm 和10cm,求连接各边中点所成三角形的周长。
A
B
C
D
E
F
6cm
8cm
10cm
AB=10cm
BC=8cm
AC=6cm
EF=5cm
DF=4cm
DE=3cm
12cm
练习
A
B
C
测出MN的长,就可知A、B两点的距离。
M
N
在AB外选一点C,使C能直接到达A和B。
连接AC和BC,并分别找出AC和BC的中点M、N。
2、若MN=36m,则AB=
2MN=72m
如果,MN两点之间还有阻隔,你有什么解决办法?
3、如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。四边形EFGH是平行四边形吗?为什么?
A
B
C
D
E
F
G
H
解:四边形EFGH是平行四边形。
连接AC,在△ABC中,
因为E、F分别是AB、BC边的中点,即EF是△ABC的中位线。
所以EF//AC,EF= AC
在△ADC中,同理可得
HG//AC,HG= AC
所以EF//HG,EF=HG
所以四边形EFGH是平行四边形。
2
1
2
1
从3中你能得到什么结论?
顺次连接四边形各边中点的线段组成一个平行四边形。
顺次连接矩形各边中点的线段组成一个 。
菱形
(1)顺次连结平行四边形各边中点所得的四边形是什么?
(2)顺次连结菱形各边中点所得的四边形是什么?
平行四边形
矩形
(3)顺次连结正方形各边中点所得的四边形是什么?
正方形
(4)顺次连结梯形各边中点所得的四边形是什么?
(5)顺次连结等腰梯形各边中点所得的四边形是什么?
平行四边形
菱形
平行四边形
正方形
平行四边形
菱形
矩形
菱形
顺次连接四边形各边中点所得到的四边形一定是平行四边形,但它是否特殊的平行四边形取决于什么呢?
议一议
拓展
(6)顺次连结对角线相等的四边形各边中点所得的四边形是什么?
(8)顺次连结对角线相等且垂直的四边形各边中点所得的四边形是什么?
(7)顺次连结对角线垂直的四边形各边中点所得的四边形是什么?
菱形
矩形
正方形
结论
原四边形两条对角线 连接四边中点所得四边形
互相垂直
矩形
相等
菱形
互相垂直且相等
正方形
既不互相垂直也不相等
平行四边形
实际上,顺次连接四边形各边中点所得到的四边形一定是平行四边形,但它是否特殊的平行四边形取决于它的对角线是否垂直或者是否相等,与是否互相平分无关。
它的对角线是否垂直
或者是否相等
它的对角线是否垂直
或者是否相等
变形题:已知E为平行四边形ABCD边的延长线上的一点,且CE=DC,连结AE,分别交BC、BD于F、G,连接AC交BD于O点,连接OF。
求证:AB=2OF。
G
证明:∵四边形ABCD是平行四边形,
∴AB=CD,OA=OC。
∴∠BAF=∠CEF,∠ABF=∠ECF。
∵CE=DC,
在平行四边形ABCD中,CD=AB,
∴AB=CE。
∴在△ABF和△ECF中,
∠BAF=∠CEFAB=CE∠ABF=∠ECF。
∴△ABF≌△ECF,
∴BF=CF,∵OA=OC,
∴OF是△ABC的中位线,
∴AB=2OF。
在四边形ABCD中,AC、BD相交于O点,AC=BD,
E、F分别是AB、CD的中点,连接EF分别交AC、BD于
M、N,判断三角形MON的形状,并说明理由。
O
连接E、 F和AD的中点G。
等腰三角形
G
EG是△ABD的中位线
GF是△ACF的中位线
∠GEF=∠GFE
∠GEF=∠ONM(AG∥BD)
∠OMN=∠GFE
(GF∥AC)
五、多边形的内、外角和
n边形共有对角线 条(n≥3)
从一个顶点出发的对角线,将n变形分成(n-2)个三角形。
1.多边形的对角线。
n边形从一个顶点出发的对角线有(n-3)条(n≥3)。
n边形的内角和为:(n-2)×180°(n≥3)。
2.多边形的内角和公式。
正n边形的每个内角
3.多边形的外角和=360°。
1.一个多边形的内角和是外角和的3倍,那么这个多边形是_____边形;这个多边形的对角线一共有_____条。
2.从一个多边形的一个顶点出发,一共作了15条对角线,则这个多边形的内角和为________度。
3.已知多边形的每个内角都是156 ,则这个多边形是_________边形。
八
20
2880
十五
4.不能铺满地面的正多边形组合是( )
A. 正三角形和正六边形 B. 正方形和正八边形
C.正三角形和正方形 D.正五边形和正六边形
D
谢 谢
第六章 平行四边形 复习课件
一、本章知识网络归纳:
多边形
内、外角和
平形四边形
三角形中位线
性质
判定
二、平行四边形的性质有:
平行四边形的对边相等。
平行四边形的对边平行。
平行四边形的对角相等。
平行四边形的对角线互相平分。
数学语言:∵在 ABCD中,∴AB=CD,AD=BC
数学语言:∵在 ABCD中,∴AB∥CD,AD∥BC
数学语言:∵在 ABCD中,∴∠B=∠D,∠A=∠C
数学语言:∵在 ABCD中,∴OB=OD,OA=OC
O
A
B
D
C
O
A
B
D
C
O
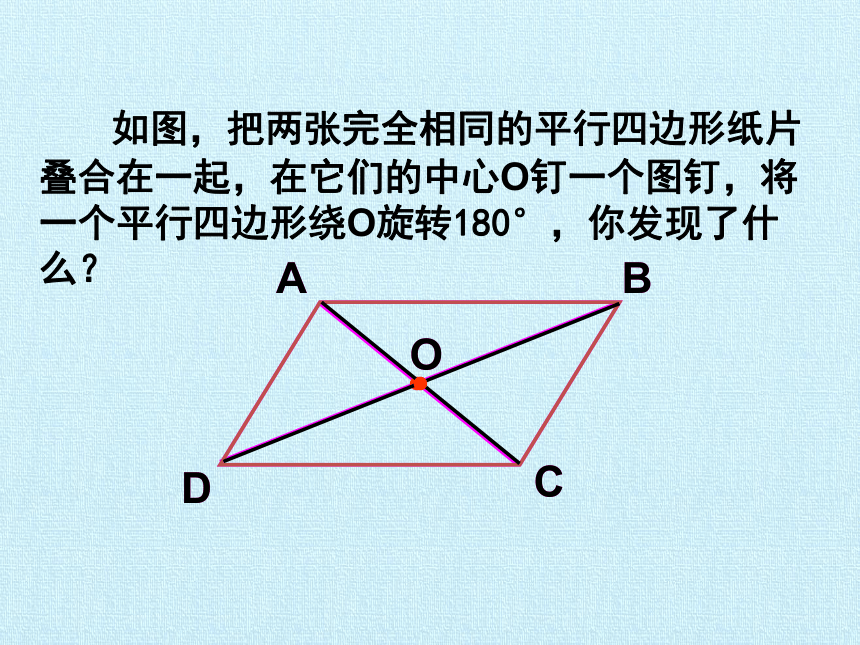
如图,把两张完全相同的平行四边形纸片叠合在一起,在它们的中心O钉一个图钉,将一个平行四边形绕O旋转180°,你发现了什么?
●
A
D
O
C
B
D
B
O
C
A
再看一遍
看一看
●
A
D
O
C
B
D
B
O
C
A
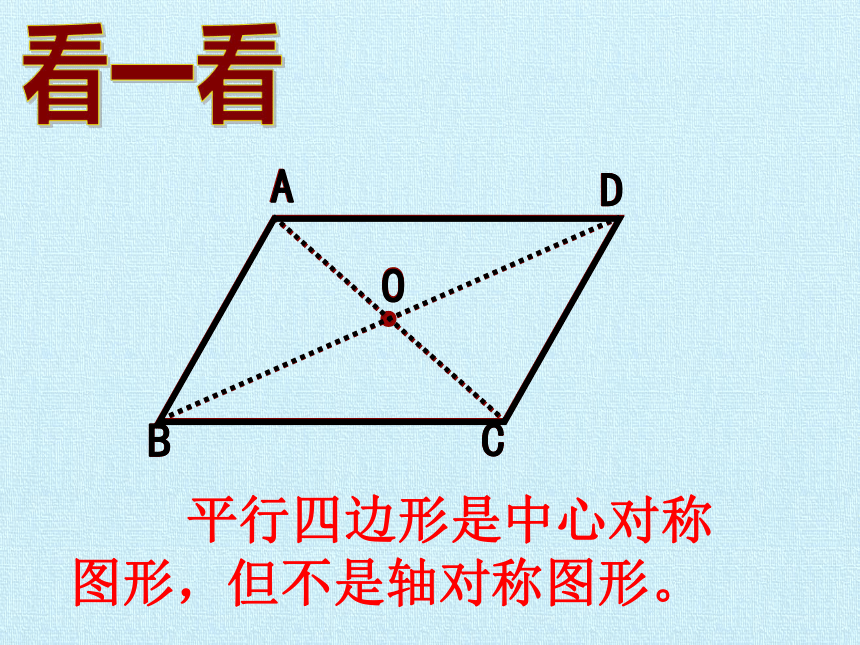
看一看
平行四边形是中心对称图形,但不是轴对称图形。
1、如图,四边形ABCD是平行四边形,AB=10,AD=8,AC⊥BC,求BC、CD、AC、OA的长以及 ABCD的面积。
8
10
B
C
D
A
●
O
解:
∴△ABC是直角三角形
又∵AC⊥BC
∵四边形ABCD是平行四边形
∴BC=AD=8,CD=AB=10
又∵OA=OC
∴
∴
∴S =BC×AC=8×6=48
ABCD
基本练习
2、如图,在 ABCD中,BC=10cm,AC=8cm,BD=14cm,
(1)△AOD的周长是多少?为什么?
(2)△ABC与△DBC的周长哪个长?长多少?
A
B
D
C
O
3、 ABCD的对角线AC与BD相交于O,直线EF过点O与AB、CD分别相交于E、F,试探究OE与OF的大小关系?并说明理由。
A
B
C
D
O
E
F
●
●
●
1
2
3
4
●
O
D
C
B
A
E
F
●
O
D
C
B
A
E
F
(1)
(2)
在上述问题中,若直线EF绕与边DA、BC的延长线交于点E、F,(如图2),上述结论是否仍然成立?试说明理由。
变式一
●
●
●
●
在上述问题中,若将直线EF绕点O旋转至下图(3)的位置时,上述结论是否仍然成立?
F
E
F
●
O
D
C
B
A
E
(1)
●
O
D
C
B
A
E
F
(3)
(3)
(4)
若此时再与两边延长线相交呢?
●
O
D
C
B
A
E
F
(4)
●
●
●
●
变式二
小结:过平行四边形的对角线交点作直线与平行四边形的一组对边或对边的延长线相交,得到线段总相等。
1.平行四边形具有而一般四边形不具有的特征是( )
A、不稳定性 B、对角线互相平分
C、内角的为360度 D、外角和为360度
B
练习题
2.若平行四边形的一边长为5,则它的两条对角线长可以是( )
A.12和2 B.3和4
C.4和6 D.4和8
D
3.如图,在平面直角坐标系中, OBCD的顶点
O、B、D的坐标如图所示,则顶点C的坐标为( )
x
Y
C
O (0,0)
B(5,0)
D(2,3)
A.(3,7) B.(5,3)
C.(7,3) D.(8,2)
C
4.如图,在 ABCD中,对角线AC,BD交于点O,AC=10,BD=8,则AD的取值范围是_________。
O
D
B
A
C
●
1<AD<9
O
D
B
A
C
5.如图,在 ABCD中,对角线AC、BD相交于点O,且AC+BD=20,△AOB的周长等于15,
则CD=______。
5
一位饱经苍桑的老人,经过一辈子的辛勤劳动,到晚年的时候,终于拥有了一块平行四边形的土地,由于年迈体弱,他决定把这块土地分给他的四个孩子,他是这样分的:
老大
老二
老三
老四
当四个孩子看到时,争论不休,都认为自己的地少,同学们,你认为老人这样分合理吗?为什么?
A
B
D
O
E
F
A
B
C
D
O
E
F
A
B
C
D
O
E
F
C
A
B
C
D
O
E
F
在这些图形中面积相等的图形有哪些?
过对角线交点的任一条直线都将平行四边形分成面积相等的两部分。
拓展
定理2:两组对边分别相等的四边形是平行四边形。
定义:两组对边分别平行的四边形是平行四边形。
定理1:一组对边平行且相等的四边形平行四边形。
三、平行四边形的判定:
定理3:对角线互相平分的四边形是平行四边形。
定理4:两组对角分别相等的四边形是平行四边形。(补充)
数学语言:∵AB∥CD,AD∥BC。∴四边形ABCD是平行四边形。
数学语言:∵AB∥CD,AB=CD。∴四边形ABCD是平行四边形。
数学语言:∵AB=CD,AD=BC。∴四边形ABCD是平行四边形。
数学语言:∵AO=CO,OD=BO。∴四边形ABCD是平行四边形。
从边来判定
1、两组对边分别平行的四边形是平行四边形
2、两组对边分别相等的四边形是平行四边形
3、一组对边平行且相等的四边形是平行四边形
从角来判定
两组对角分别相等的四边形是平行四边形
从对角线来判定
两条对角线互相平分的四边形是平行四边形
理一理
平行四边形的判定方法
1、如图,已知AC是□ABCD的一条对角线,BM⊥AC
于M,DN⊥AC于N,求证:四边形BMDN是平行四边形。
证明:连接BD交AC于O。
∵BM⊥AC于M,DN⊥AC于N,
∴∠AND=∠CMB=90°。
∵四边形ABCD是平行四边形,
∴OB=OD,OA=OC,AD CB。
∴∠DAN=∠BCM
∴△ADN≌△CBM
∴AN=CM。
∴OA-AN=OC-CM,
即ON=OM
∴四边形BMDN是平行四边形。
∥
=
2、在四边形ABCD中,对角线AC、BD交于O点,且OA=OC,OB=OD,△AOD的周长比△AOB的周长4cm,AD:AB=2:1,求四边形ABCD的周长。
解:∵OA=OC,OB=OD
∴ABCD是平行四边形
△AOD的周长=AD+OA+OD
△AOB的周长=AB+OA+OB
△AOD的周长比△AOB的周长多4cm,
即(AD+OA+OD)-(AB+OA+OB)=4cm
化简得AD-AB=4cm,又因为AD:AB=2:1
∴AD=8cm,AB=4cm
平行四边形ABCD周长=(8+4)×2=24cm
O
D
C
B
A
1、已知:如图,在平行四边形ABCD中,E,F分别是
AB,DC上的两点,且AE=CF。
求证:BD,EF互相平分。
快速解答:
2、已知:如图,在平行四边形ABCD中,点M,N在对角线AC上,且AM=CN。
求证:四边形BMDN是平行四边形。
3、已知:如图,在平行四边形ABCD中,E,F分别是AB,CD上的两点,且AE=CF,AF,DE相交于点M,BF,CE相交于点N。
求证:四边形EMFN是平行四边形。
N
M
B
A
C
D
E
F
三角形的中位线平行于第三边,并且等于第三边的一半。
四、三角形的中位线
A
B
C
D
E
数学语言:∵DE是△ABC的中位线∴DE= ,DE∥BC。
1、三角形各边的长分别为6cm、8cm 和10cm,求连接各边中点所成三角形的周长。
A
B
C
D
E
F
6cm
8cm
10cm
AB=10cm
BC=8cm
AC=6cm
EF=5cm
DF=4cm
DE=3cm
12cm
练习
A
B
C
测出MN的长,就可知A、B两点的距离。
M
N
在AB外选一点C,使C能直接到达A和B。
连接AC和BC,并分别找出AC和BC的中点M、N。
2、若MN=36m,则AB=
2MN=72m
如果,MN两点之间还有阻隔,你有什么解决办法?
3、如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。四边形EFGH是平行四边形吗?为什么?
A
B
C
D
E
F
G
H
解:四边形EFGH是平行四边形。
连接AC,在△ABC中,
因为E、F分别是AB、BC边的中点,即EF是△ABC的中位线。
所以EF//AC,EF= AC
在△ADC中,同理可得
HG//AC,HG= AC
所以EF//HG,EF=HG
所以四边形EFGH是平行四边形。
2
1
2
1
从3中你能得到什么结论?
顺次连接四边形各边中点的线段组成一个平行四边形。
顺次连接矩形各边中点的线段组成一个 。
菱形
(1)顺次连结平行四边形各边中点所得的四边形是什么?
(2)顺次连结菱形各边中点所得的四边形是什么?
平行四边形
矩形
(3)顺次连结正方形各边中点所得的四边形是什么?
正方形
(4)顺次连结梯形各边中点所得的四边形是什么?
(5)顺次连结等腰梯形各边中点所得的四边形是什么?
平行四边形
菱形
平行四边形
正方形
平行四边形
菱形
矩形
菱形
顺次连接四边形各边中点所得到的四边形一定是平行四边形,但它是否特殊的平行四边形取决于什么呢?
议一议
拓展
(6)顺次连结对角线相等的四边形各边中点所得的四边形是什么?
(8)顺次连结对角线相等且垂直的四边形各边中点所得的四边形是什么?
(7)顺次连结对角线垂直的四边形各边中点所得的四边形是什么?
菱形
矩形
正方形
结论
原四边形两条对角线 连接四边中点所得四边形
互相垂直
矩形
相等
菱形
互相垂直且相等
正方形
既不互相垂直也不相等
平行四边形
实际上,顺次连接四边形各边中点所得到的四边形一定是平行四边形,但它是否特殊的平行四边形取决于它的对角线是否垂直或者是否相等,与是否互相平分无关。
它的对角线是否垂直
或者是否相等
它的对角线是否垂直
或者是否相等
变形题:已知E为平行四边形ABCD边的延长线上的一点,且CE=DC,连结AE,分别交BC、BD于F、G,连接AC交BD于O点,连接OF。
求证:AB=2OF。
G
证明:∵四边形ABCD是平行四边形,
∴AB=CD,OA=OC。
∴∠BAF=∠CEF,∠ABF=∠ECF。
∵CE=DC,
在平行四边形ABCD中,CD=AB,
∴AB=CE。
∴在△ABF和△ECF中,
∠BAF=∠CEFAB=CE∠ABF=∠ECF。
∴△ABF≌△ECF,
∴BF=CF,∵OA=OC,
∴OF是△ABC的中位线,
∴AB=2OF。
在四边形ABCD中,AC、BD相交于O点,AC=BD,
E、F分别是AB、CD的中点,连接EF分别交AC、BD于
M、N,判断三角形MON的形状,并说明理由。
O
连接E、 F和AD的中点G。
等腰三角形
G
EG是△ABD的中位线
GF是△ACF的中位线
∠GEF=∠GFE
∠GEF=∠ONM(AG∥BD)
∠OMN=∠GFE
(GF∥AC)
五、多边形的内、外角和
n边形共有对角线 条(n≥3)
从一个顶点出发的对角线,将n变形分成(n-2)个三角形。
1.多边形的对角线。
n边形从一个顶点出发的对角线有(n-3)条(n≥3)。
n边形的内角和为:(n-2)×180°(n≥3)。
2.多边形的内角和公式。
正n边形的每个内角
3.多边形的外角和=360°。
1.一个多边形的内角和是外角和的3倍,那么这个多边形是_____边形;这个多边形的对角线一共有_____条。
2.从一个多边形的一个顶点出发,一共作了15条对角线,则这个多边形的内角和为________度。
3.已知多边形的每个内角都是156 ,则这个多边形是_________边形。
八
20
2880
十五
4.不能铺满地面的正多边形组合是( )
A. 正三角形和正六边形 B. 正方形和正八边形
C.正三角形和正方形 D.正五边形和正六边形
D
谢 谢
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
