2021-2022学年人教版七年级数学上册 3.3解一元一次方程 第2课时 利用去分母解一元一次方程
文档属性
| 名称 | 2021-2022学年人教版七年级数学上册 3.3解一元一次方程 第2课时 利用去分母解一元一次方程 |  | |
| 格式 | zip | ||
| 文件大小 | 729.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 21:30:25 | ||
图片预览







文档简介
(共26张PPT)
第三章 一元一次方程
3.2 解一元一次方程(二)
第2课时 利用去分母解一元一次方程
学 习 目 标
掌握去分母解方程的方法,总结解方程的步骤.(重点)
经历去分母解方程的过程,体会把“复杂”转化为“简单”,把“新”转化为“旧”的转化的思想方法.(难点)
1
2
温故知新
解:去括号,得 4x+2=1-5x+10
移项,得 4x+5x=1+10-2
合并同类项,得 9x=9
系数化为1,得 x=1
解下列方程:
2(2x+1)=1-5(x-2)
新课导入
丢番图的墓志铭
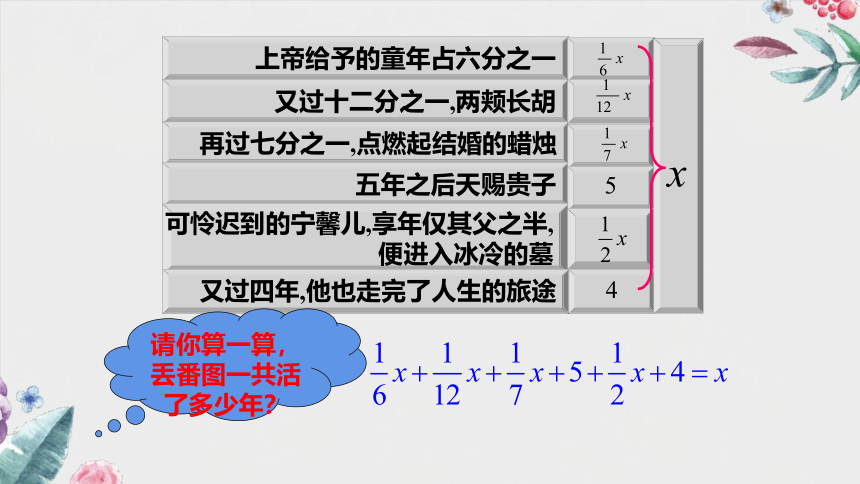
墓中长眠着一个伟大的人物——丢番图
他的一生的六分之一时光,是童年时代; 又度过了十二分之一岁月后, 他满脸长出了胡须;再过了七分之一年月时, 举行了花烛盛典;婚后五年, 得一贵子。可是不幸的孩子,他仅仅活了父亲的半生时光,就离开了人间。 从此,作为父亲的丢番图,在悲伤中度过了四年后, 结束了自己的一生。
你能算出丢番图生活的岁数吗?
可设他生活的岁数 为x,则:
上帝给予的童年占六分之一
又过十二分之一,两颊长胡
再过七分之一,点燃起结婚的蜡烛
五年之后天赐贵子
可怜迟到的宁馨儿,享年仅其父之半,
便进入冰冷的墓
又过四年,他也走完了人生的旅途
请你算一算,丢番图一共活了多少年?
这个方程你会解吗?
像这样的方程中
有些系数是分数,
如果能化去分母,
把系数化为整数,
则可以使解方程中
的计算更方便些。
去分母,得
14x+7x+12x+420+42x+336=84x
方法2:
方程两边同乘各分母的最小公倍数,则得到
移项,得
14x+7x+12x+42x-84x=- 420 – 336
合并同类项,得 - 9X= - 756
系数化这1.得 X=84
总结:像上面这样的方程中有些系数是分数,如果能化去分母,把系数化为整数,则可以使解方程中的计算更方便些.
知识讲解
解含分母的一元一次方程
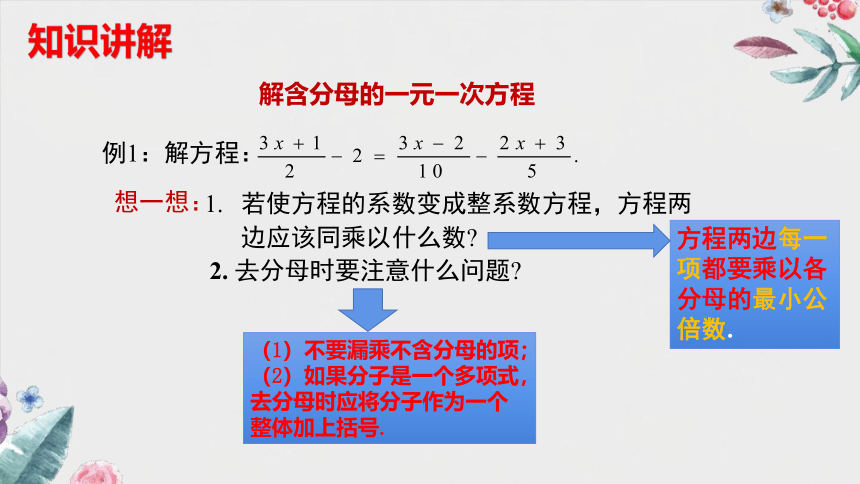
例1:解方程:
2. 去分母时要注意什么问题
想一想:
若使方程的系数变成整系数方程,方程两边应该同乘以什么数
方程两边每一项都要乘以各分母的最小公倍数.
(1)不要漏乘不含分母的项;(2)如果分子是一个多项式,去分母时应将分子作为一个整体加上括号.
系数化为1
去分母(方程两边同乘各分母的最小公倍数)
移项
合并同类项
去括号
小心漏乘不含分母的项,分式是多项式的,记得添括号!
解一元一次方程的一般步骤为:去分母,去括号,移项,合并同类项,系数化为1.注意这些步骤不是固定不变的,有时可以省略某个步骤,要根据方程的特点灵活选用.
归纳:
去分母解方程应注意:
(a)所选的乘数是方程中所有分母的最小公倍数,不应遗漏;
(b)用各分母的最小公倍数乘方程的两边时,不要遗漏方程中不含分母的项;
(c)去掉分母后,分数线也同时去掉,分子上的多项式要用括号括起来.
练一练
20
3.解下列方程
去分母,得
2(x+1)-4=8+(2-x)
去括号,得
2x+2-4=8+2-x
移项,得
2x+x=8+2-2+4
合并同类项,得
3x=12
系数化为1,得
练一练
练一练
去分母,得
18x+3( x-l)=18-2(2x-1)
去括号,得
18x+3x-3=18-4x+2
移项,得
18x+3x+4x=18+2+3
合并同类项,得
25x=23
系数化为1,得
去分母解一元一次方程的步骤
步骤 具体做法 依据 注意事项
去分母 在方程两边都乘以各分母的最小公倍数 等式性质2 不要漏乘不含分母的项
去括号 一般先去小括号,再去中括号,最后去大括号 分配律 去括号法则 不要漏乘括号中的每一项
移项 把含有未知数的项移到方程一边,其它项都移到方程另一边,注意移项要变号 等式性质1 1)移动的项一定要变号,
不移的项不变号
2)注意项较多时不要漏项
合并同类项 把方程变为ax=b (a≠0 ) 的最简形式 合并同类项法则 1)把系数相加
2)字母和字母的指数不变
系数化为1 等式性质2 解的分子,分母位置不要颠倒
去分母解方程的应用
例 火车用26秒的时间通过一个长256米的隧道(即从车头进入入口到车尾离开出口),这列火车又以16秒的时间通过了长96米的隧道,求火车的长度.
解:设火车的长度为x米,根据题意,列方程,得
解得 x =160.
答:火车的长度为160米.
有一人问老师,他所教的班级有多少学生,老师说:“一半学生在学数学,四分之一的学生在学音乐,七分之一的学生在学外语,还剩六位学生正在操场踢足球.”你知道这个班有多少学生吗?
答:这个班有56个学生.
解:这个班有x名学生,依题意,得
解得x=56.
练一练
随堂训练
1.将方程 去分母时,方程两边同时乘( )
A.4 B.6 C.8 D.12
A
【解析】找出方程各分母的最小公倍数即可得
到结果.因为2和4的最小公倍数是4,
所以去分母时两边应同时乘4。
2.对于方程 ,变形第一步较好的 办法是( )
A.移项 B.去括号 C.去分母 D.合并同类项
C
【解析】方程两边乘4去分母,再乘6去分母后,去括号、移项、合并同类项、将x系数化为1即可求解,所以第一步去分母较好。
C
3. 方程 去分母正确的是 ( )
A. 3-2(5x+7) = -(x+17)
B. 12-2(5x+7) = -x+17
C. 12-2(5x+7) = -(x+17)
D. 12-10x+14 = -(x+17)
4. 若代数式 与 的值互为倒数,则x= .
5.小明在做解方程的作业时,不小心将方程中的一个常数
污染了看不清楚,被污染的方程是2y- = y-■,
怎么办呢 小明想了一想,便翻看了书后的答案,此方程
的解是y=- .很快补好了这个常数,这个常数应
是_____.
6.某书中一道方程题 , 处印刷时被墨盖住了,查后面的答案,这道题的解为x=﹣2.5,那么 处的数为( )
A.﹣2.5 B.2.5 C.3.5 D.5
【解析】设 =a,把方程去分母得:2+ax+3=3x,3x﹣ax=5,把x=﹣2.5代入方程得:3×(﹣2.5)﹣(﹣2.5)a=5,解得a=5.
D
7.解下列方程:
解;(1)去分母(方程两边同乘6),得
(x-1) -2(2x+1) = 6.
去括号,得 x-1-4x-2 = 6.
移项,得 x-4x = 6+2+1.
合并同类项,得-3x = 9.
系数化为1,得 x = -3.
(2)去分母(方程两边同乘30),得
6 (4x+9) -10(3+2x) = 15(x-5).
去括号,得 24x+54-30-20x = 15x-75.
移项,得24x-20x-15x =-75-54+30 .
合并同类项,得-11x = -99.
系数化为1,得 x = 9.
8. 某单位计划“五一”期间组织职工外出旅游,如果单独租用40座的客车若干辆刚好坐满;如果租用50座的客车则可以少租一辆,并且有40个剩余座位.该单位参加旅游的职工有多少人?
解:设该单位参加旅游的职工有x人,由题意,得
解得x=360.
答:该单位参加旅游的职工有360人.
议一议:如何解方程
解:分别将分子分母扩大10倍(根据分数的基本性质),得
分子分母约分,得
去括号,得
移项,得
合并同类项,得
系数化为1,得
课堂小结
步骤 具体做法 依据 注意事项
去分母 在方程两边都乘以各分母的最小公倍数 等式性质2 不要漏乘不含分母的项
去括号 一般先去小括号,再去中括号,最后去大括号 分配律 去括号法则 不要漏乘括号中的每一项
移项 把含有未知数的项移到方程一边,其它项都移到方程另一边,注意移项要变号 等式性质1 1)移动的项一定要变号,
不移的项不变号
2)注意项较多时不要漏项
合并同类项 把方程变为ax=b (a≠0 ) 的最简形式 合并同类项法则 1)把系数相加
2)字母和字母的指数不变
系数化为1 等式性质2 解的分子,分母位置不要颠倒
第三章 一元一次方程
3.2 解一元一次方程(二)
第2课时 利用去分母解一元一次方程
学 习 目 标
掌握去分母解方程的方法,总结解方程的步骤.(重点)
经历去分母解方程的过程,体会把“复杂”转化为“简单”,把“新”转化为“旧”的转化的思想方法.(难点)
1
2
温故知新
解:去括号,得 4x+2=1-5x+10
移项,得 4x+5x=1+10-2
合并同类项,得 9x=9
系数化为1,得 x=1
解下列方程:
2(2x+1)=1-5(x-2)
新课导入
丢番图的墓志铭
墓中长眠着一个伟大的人物——丢番图
他的一生的六分之一时光,是童年时代; 又度过了十二分之一岁月后, 他满脸长出了胡须;再过了七分之一年月时, 举行了花烛盛典;婚后五年, 得一贵子。可是不幸的孩子,他仅仅活了父亲的半生时光,就离开了人间。 从此,作为父亲的丢番图,在悲伤中度过了四年后, 结束了自己的一生。
你能算出丢番图生活的岁数吗?
可设他生活的岁数 为x,则:
上帝给予的童年占六分之一
又过十二分之一,两颊长胡
再过七分之一,点燃起结婚的蜡烛
五年之后天赐贵子
可怜迟到的宁馨儿,享年仅其父之半,
便进入冰冷的墓
又过四年,他也走完了人生的旅途
请你算一算,丢番图一共活了多少年?
这个方程你会解吗?
像这样的方程中
有些系数是分数,
如果能化去分母,
把系数化为整数,
则可以使解方程中
的计算更方便些。
去分母,得
14x+7x+12x+420+42x+336=84x
方法2:
方程两边同乘各分母的最小公倍数,则得到
移项,得
14x+7x+12x+42x-84x=- 420 – 336
合并同类项,得 - 9X= - 756
系数化这1.得 X=84
总结:像上面这样的方程中有些系数是分数,如果能化去分母,把系数化为整数,则可以使解方程中的计算更方便些.
知识讲解
解含分母的一元一次方程
例1:解方程:
2. 去分母时要注意什么问题
想一想:
若使方程的系数变成整系数方程,方程两边应该同乘以什么数
方程两边每一项都要乘以各分母的最小公倍数.
(1)不要漏乘不含分母的项;(2)如果分子是一个多项式,去分母时应将分子作为一个整体加上括号.
系数化为1
去分母(方程两边同乘各分母的最小公倍数)
移项
合并同类项
去括号
小心漏乘不含分母的项,分式是多项式的,记得添括号!
解一元一次方程的一般步骤为:去分母,去括号,移项,合并同类项,系数化为1.注意这些步骤不是固定不变的,有时可以省略某个步骤,要根据方程的特点灵活选用.
归纳:
去分母解方程应注意:
(a)所选的乘数是方程中所有分母的最小公倍数,不应遗漏;
(b)用各分母的最小公倍数乘方程的两边时,不要遗漏方程中不含分母的项;
(c)去掉分母后,分数线也同时去掉,分子上的多项式要用括号括起来.
练一练
20
3.解下列方程
去分母,得
2(x+1)-4=8+(2-x)
去括号,得
2x+2-4=8+2-x
移项,得
2x+x=8+2-2+4
合并同类项,得
3x=12
系数化为1,得
练一练
练一练
去分母,得
18x+3( x-l)=18-2(2x-1)
去括号,得
18x+3x-3=18-4x+2
移项,得
18x+3x+4x=18+2+3
合并同类项,得
25x=23
系数化为1,得
去分母解一元一次方程的步骤
步骤 具体做法 依据 注意事项
去分母 在方程两边都乘以各分母的最小公倍数 等式性质2 不要漏乘不含分母的项
去括号 一般先去小括号,再去中括号,最后去大括号 分配律 去括号法则 不要漏乘括号中的每一项
移项 把含有未知数的项移到方程一边,其它项都移到方程另一边,注意移项要变号 等式性质1 1)移动的项一定要变号,
不移的项不变号
2)注意项较多时不要漏项
合并同类项 把方程变为ax=b (a≠0 ) 的最简形式 合并同类项法则 1)把系数相加
2)字母和字母的指数不变
系数化为1 等式性质2 解的分子,分母位置不要颠倒
去分母解方程的应用
例 火车用26秒的时间通过一个长256米的隧道(即从车头进入入口到车尾离开出口),这列火车又以16秒的时间通过了长96米的隧道,求火车的长度.
解:设火车的长度为x米,根据题意,列方程,得
解得 x =160.
答:火车的长度为160米.
有一人问老师,他所教的班级有多少学生,老师说:“一半学生在学数学,四分之一的学生在学音乐,七分之一的学生在学外语,还剩六位学生正在操场踢足球.”你知道这个班有多少学生吗?
答:这个班有56个学生.
解:这个班有x名学生,依题意,得
解得x=56.
练一练
随堂训练
1.将方程 去分母时,方程两边同时乘( )
A.4 B.6 C.8 D.12
A
【解析】找出方程各分母的最小公倍数即可得
到结果.因为2和4的最小公倍数是4,
所以去分母时两边应同时乘4。
2.对于方程 ,变形第一步较好的 办法是( )
A.移项 B.去括号 C.去分母 D.合并同类项
C
【解析】方程两边乘4去分母,再乘6去分母后,去括号、移项、合并同类项、将x系数化为1即可求解,所以第一步去分母较好。
C
3. 方程 去分母正确的是 ( )
A. 3-2(5x+7) = -(x+17)
B. 12-2(5x+7) = -x+17
C. 12-2(5x+7) = -(x+17)
D. 12-10x+14 = -(x+17)
4. 若代数式 与 的值互为倒数,则x= .
5.小明在做解方程的作业时,不小心将方程中的一个常数
污染了看不清楚,被污染的方程是2y- = y-■,
怎么办呢 小明想了一想,便翻看了书后的答案,此方程
的解是y=- .很快补好了这个常数,这个常数应
是_____.
6.某书中一道方程题 , 处印刷时被墨盖住了,查后面的答案,这道题的解为x=﹣2.5,那么 处的数为( )
A.﹣2.5 B.2.5 C.3.5 D.5
【解析】设 =a,把方程去分母得:2+ax+3=3x,3x﹣ax=5,把x=﹣2.5代入方程得:3×(﹣2.5)﹣(﹣2.5)a=5,解得a=5.
D
7.解下列方程:
解;(1)去分母(方程两边同乘6),得
(x-1) -2(2x+1) = 6.
去括号,得 x-1-4x-2 = 6.
移项,得 x-4x = 6+2+1.
合并同类项,得-3x = 9.
系数化为1,得 x = -3.
(2)去分母(方程两边同乘30),得
6 (4x+9) -10(3+2x) = 15(x-5).
去括号,得 24x+54-30-20x = 15x-75.
移项,得24x-20x-15x =-75-54+30 .
合并同类项,得-11x = -99.
系数化为1,得 x = 9.
8. 某单位计划“五一”期间组织职工外出旅游,如果单独租用40座的客车若干辆刚好坐满;如果租用50座的客车则可以少租一辆,并且有40个剩余座位.该单位参加旅游的职工有多少人?
解:设该单位参加旅游的职工有x人,由题意,得
解得x=360.
答:该单位参加旅游的职工有360人.
议一议:如何解方程
解:分别将分子分母扩大10倍(根据分数的基本性质),得
分子分母约分,得
去括号,得
移项,得
合并同类项,得
系数化为1,得
课堂小结
步骤 具体做法 依据 注意事项
去分母 在方程两边都乘以各分母的最小公倍数 等式性质2 不要漏乘不含分母的项
去括号 一般先去小括号,再去中括号,最后去大括号 分配律 去括号法则 不要漏乘括号中的每一项
移项 把含有未知数的项移到方程一边,其它项都移到方程另一边,注意移项要变号 等式性质1 1)移动的项一定要变号,
不移的项不变号
2)注意项较多时不要漏项
合并同类项 把方程变为ax=b (a≠0 ) 的最简形式 合并同类项法则 1)把系数相加
2)字母和字母的指数不变
系数化为1 等式性质2 解的分子,分母位置不要颠倒
