2021-2022学年九年级数学上册人教版23.1图形的旋转课件(共17张PPT)
文档属性
| 名称 | 2021-2022学年九年级数学上册人教版23.1图形的旋转课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 17.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 23:32:35 | ||
图片预览




文档简介
(共17张PPT)
23.1图形的旋转
日日奇闻
在我们的生活中类似旋转大楼一样能够转动的物体随处可见,你能举出一些例子吗
看一看:观察下图中图形的运动,试着发现它们的规律.
认识旋转
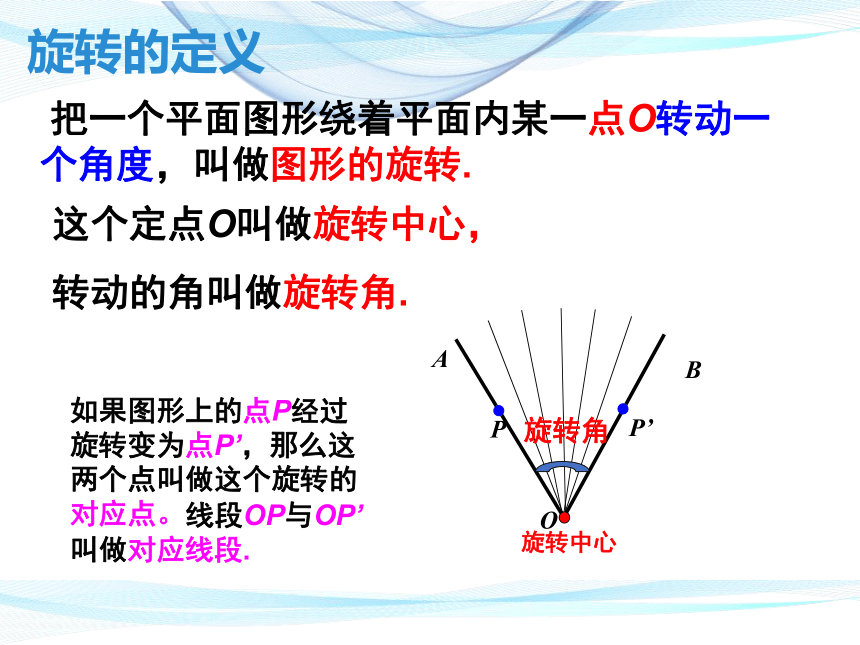
这个定点O叫做旋转中心,
转动的角叫做旋转角.
旋转角
旋转中心
把一个平面图形绕着平面内某一点O转动一个角度,叫做图形的旋转.
A
O
B
P
P’
如果图形上的点P经过旋转变为点P’,那么这两个点叫做这个旋转的对应点。
线段OP与OP’叫做对应线段.
旋转的定义
学以致用
下列现象中属于旋转的有( )个
①地下水位逐年下降;②传送带上的机器人;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
A.2 B.3 C.4 D.5
C
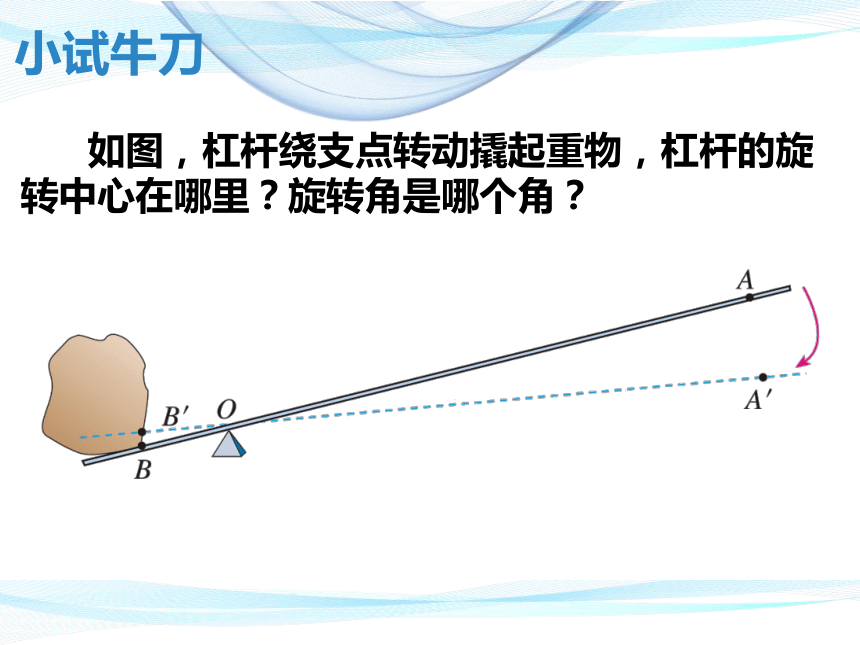
如图,杠杆绕支点转动撬起重物,杠杆的旋转中心在哪里?旋转角是哪个角?
小试牛刀
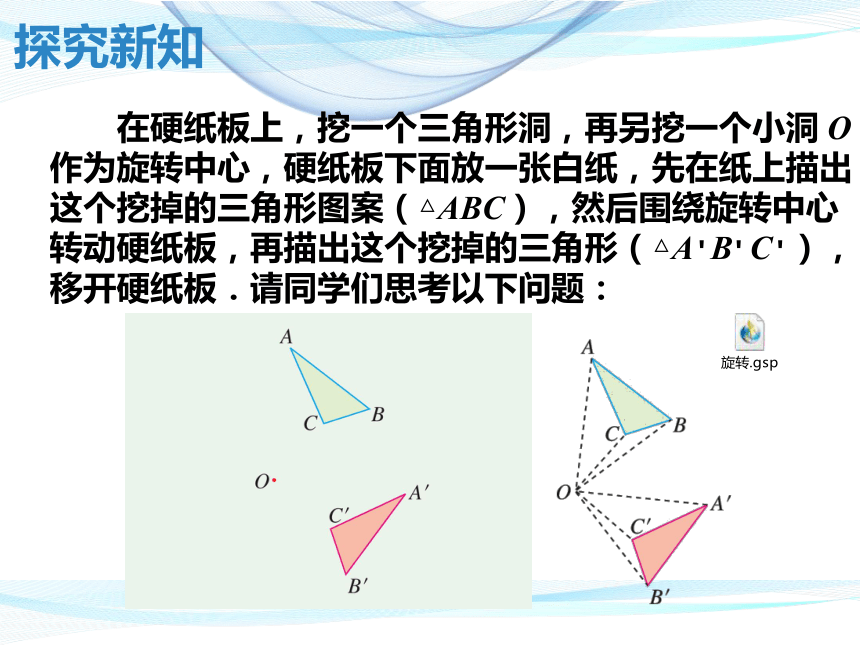
探究新知
在硬纸板上,挖一个三角形洞,再另挖一个小洞 O
作为旋转中心,硬纸板下面放一张白纸,先在纸上描出
这个挖掉的三角形图案(△ABC),然后围绕旋转中心
转动硬纸板,再描出这个挖掉的三角形(△A B C ),
移开硬纸板.请同学们思考以下问题:
'
'
'
旋转的性质
探究发现
◆ 对应点到旋转中心的距离相等.
◆ 对应点与旋转中心所连线段的夹角等于旋转角.
◆ 旋转前、后的图形全等.
点A
顺时针
∠BAE或∠CAD
AD
ED
∠AED
(5)连接CD,试判断△ACD的形状.
性质应用
【例】如图,△ABC旋转后与△AED重合,且△ABE为等边三角形,那么:
(1)旋转中心是__________;
(2)旋转方向是__________;
(3)旋转角是_________________;
(4)AC的对应线段是__________,BC的对应线段是______,∠ABC的对应角是__________;
解:△ACD是等边三角形.
1.将如图所示的图案以圆心为中心,旋转180°后得到的图案是( )
D
课堂检测
课堂检测
2.△ABC绕点A旋转一定角度后得到△ADE,若BC=4,AC=3,则下列说法正确的是( )
A. DE=3
B. AE=4
C. ∠CAB是旋转角
D. ∠CAE是旋转角
D
3
5
44 °
课堂检测
3. △A ′ OB ′是△AOB绕点O按逆时针方向旋转得到的.已知∠AOB=20 °, ∠ A ′ OB =24°,
AB=3,OA=5,则A ′ B ′ = ,OA ′ = ,
旋转角等于 .
课堂回顾:这节课,主要学习了什么?
1、旋转的概念:
把一个平面图形绕着平面内某一点O转动一个角度,叫做图形的旋转.
2、旋转三要素:
旋转中心、旋转角度、旋转方向.
3、旋转的性质:
①旋转前后的图形全等;
②对应点到旋转中心的距离相等;
③对应点与旋转中心所连线段的夹角等于旋转角.
1.如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接BB′,若∠A′B′B=20°,则∠A的度数是__________.
2.如图,在矩形ABCD中,AD=3,将矩形ABCD绕点A逆时针旋转,得到矩形AEFG,点B的对应点E落在CD上,且DE=EF,则AB的长为________.
65°
32
课后作业
3.如图,四边形ABCD是边长为1的正方形,且DE=14,△ABF是△ADE的旋转图形.
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)AF的长度是多少?
(4)如果连接EF,那么△AEF是什么三角形?
解 (1)旋转中心是点A.
(2)旋转了90°.
(4)△AEF是等腰直角三角形.
(3)AF= .
课后作业
4.如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△AB′C′的位置,使得CC′∥AB,求∠CAB′的度数.
∴∠CAB′=∠C′AB′-∠C′AC=30°.
解 由旋转的性质可知
AC=AC′,∠C′AB′=∠CAB=70°,
∴∠AC′C=∠ACC′.
∵CC′∥AB,
∴∠ACC′=∠CAB=70°,
∴∠C′AC=40°,
课后作业
谢 谢
23.1图形的旋转
日日奇闻
在我们的生活中类似旋转大楼一样能够转动的物体随处可见,你能举出一些例子吗
看一看:观察下图中图形的运动,试着发现它们的规律.
认识旋转
这个定点O叫做旋转中心,
转动的角叫做旋转角.
旋转角
旋转中心
把一个平面图形绕着平面内某一点O转动一个角度,叫做图形的旋转.
A
O
B
P
P’
如果图形上的点P经过旋转变为点P’,那么这两个点叫做这个旋转的对应点。
线段OP与OP’叫做对应线段.
旋转的定义
学以致用
下列现象中属于旋转的有( )个
①地下水位逐年下降;②传送带上的机器人;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动.
A.2 B.3 C.4 D.5
C
如图,杠杆绕支点转动撬起重物,杠杆的旋转中心在哪里?旋转角是哪个角?
小试牛刀
探究新知
在硬纸板上,挖一个三角形洞,再另挖一个小洞 O
作为旋转中心,硬纸板下面放一张白纸,先在纸上描出
这个挖掉的三角形图案(△ABC),然后围绕旋转中心
转动硬纸板,再描出这个挖掉的三角形(△A B C ),
移开硬纸板.请同学们思考以下问题:
'
'
'
旋转的性质
探究发现
◆ 对应点到旋转中心的距离相等.
◆ 对应点与旋转中心所连线段的夹角等于旋转角.
◆ 旋转前、后的图形全等.
点A
顺时针
∠BAE或∠CAD
AD
ED
∠AED
(5)连接CD,试判断△ACD的形状.
性质应用
【例】如图,△ABC旋转后与△AED重合,且△ABE为等边三角形,那么:
(1)旋转中心是__________;
(2)旋转方向是__________;
(3)旋转角是_________________;
(4)AC的对应线段是__________,BC的对应线段是______,∠ABC的对应角是__________;
解:△ACD是等边三角形.
1.将如图所示的图案以圆心为中心,旋转180°后得到的图案是( )
D
课堂检测
课堂检测
2.△ABC绕点A旋转一定角度后得到△ADE,若BC=4,AC=3,则下列说法正确的是( )
A. DE=3
B. AE=4
C. ∠CAB是旋转角
D. ∠CAE是旋转角
D
3
5
44 °
课堂检测
3. △A ′ OB ′是△AOB绕点O按逆时针方向旋转得到的.已知∠AOB=20 °, ∠ A ′ OB =24°,
AB=3,OA=5,则A ′ B ′ = ,OA ′ = ,
旋转角等于 .
课堂回顾:这节课,主要学习了什么?
1、旋转的概念:
把一个平面图形绕着平面内某一点O转动一个角度,叫做图形的旋转.
2、旋转三要素:
旋转中心、旋转角度、旋转方向.
3、旋转的性质:
①旋转前后的图形全等;
②对应点到旋转中心的距离相等;
③对应点与旋转中心所连线段的夹角等于旋转角.
1.如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接BB′,若∠A′B′B=20°,则∠A的度数是__________.
2.如图,在矩形ABCD中,AD=3,将矩形ABCD绕点A逆时针旋转,得到矩形AEFG,点B的对应点E落在CD上,且DE=EF,则AB的长为________.
65°
32
课后作业
3.如图,四边形ABCD是边长为1的正方形,且DE=14,△ABF是△ADE的旋转图形.
(1)旋转中心是哪一点?
(2)旋转了多少度?
(3)AF的长度是多少?
(4)如果连接EF,那么△AEF是什么三角形?
解 (1)旋转中心是点A.
(2)旋转了90°.
(4)△AEF是等腰直角三角形.
(3)AF= .
课后作业
4.如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△AB′C′的位置,使得CC′∥AB,求∠CAB′的度数.
∴∠CAB′=∠C′AB′-∠C′AC=30°.
解 由旋转的性质可知
AC=AC′,∠C′AB′=∠CAB=70°,
∴∠AC′C=∠ACC′.
∵CC′∥AB,
∴∠ACC′=∠CAB=70°,
∴∠C′AC=40°,
课后作业
谢 谢
同课章节目录
