2021-2022学年九年级数学北师大版上册6.2.1反比例函数的图像与性质课件(一)(共20张PPT)
文档属性
| 名称 | 2021-2022学年九年级数学北师大版上册6.2.1反比例函数的图像与性质课件(一)(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 577.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 23:39:22 | ||
图片预览




文档简介
(共20张PPT)
6.2.1 反比例函数的图像与性质(一)
第六章 反比例函数
温故知新
一般地,如果两个变量x,y之间的对应关系可以表示成:
的形式,那么称y是x的反比例函数.
y=
k
x
(k 为常数,k≠0)
反比例函数:
反比例函数表达式的三种常见形式:
y=
k
x
(k 为常数,k≠0)
xy=k
y=k
-1
x
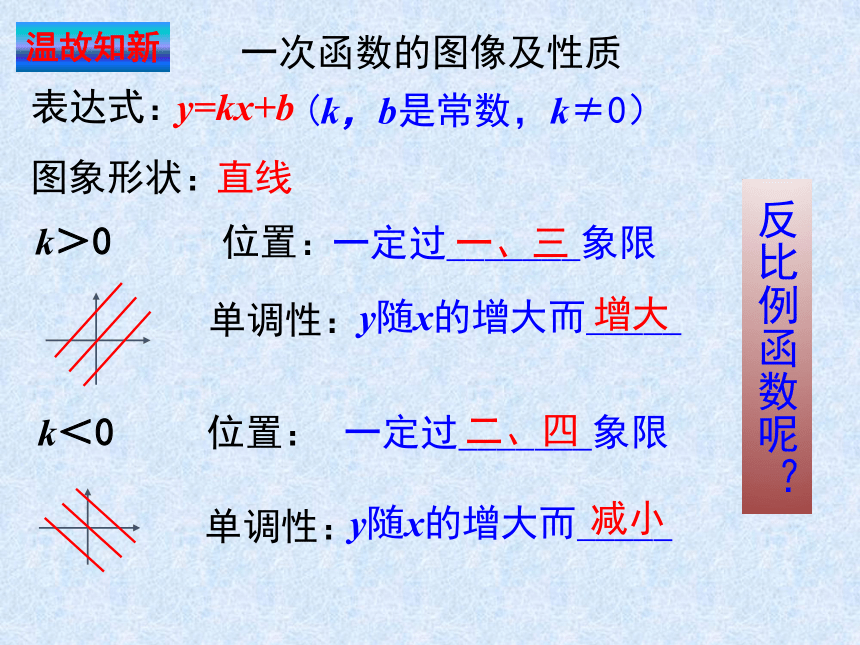
一次函数的图像及性质
温故知新
表达式:
图象形状:
位置:
y=kx+b
直线
一定过_______象限
y随x的增大而_____
一定过_______象限
y随x的增大而_____
单调性:
k>0
k<0
位置:
单调性:
反比例函数呢?
(k,b是常数,k≠0)
一、三
二、四
增大
减小
温故知新
如何画函数的图象?
描点法:
列表
描点
连线
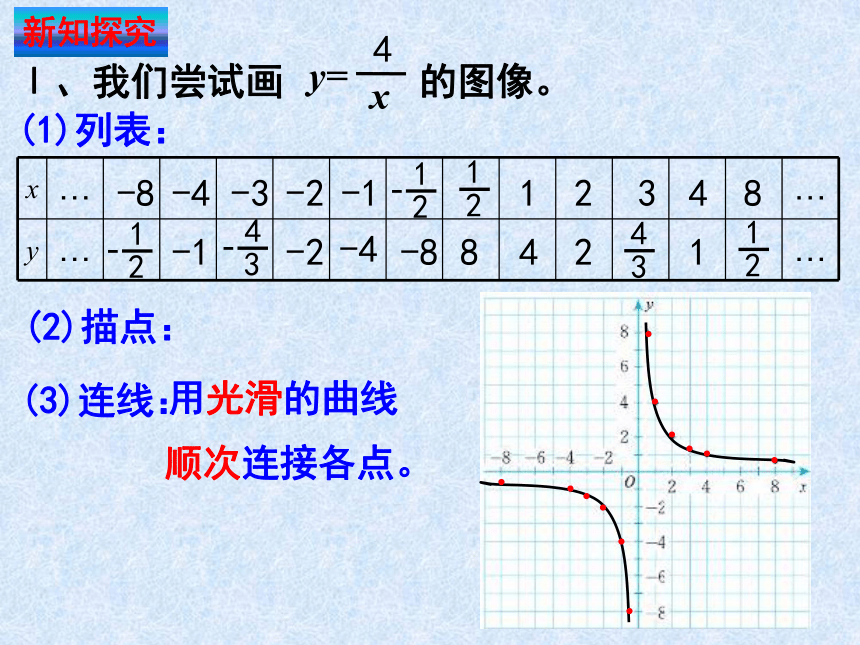
Ⅰ、我们尝试画 的图像。
(1)列表:
x … …
y … …
(2)描点:
(3)连线:
用光滑的曲线
-8
-4
-3
-2
-1
1
2
3
4
8
-1
-2
-4
-8
8
4
2
1
·
·
·
·
·
·
·
·
·
·
·
·
顺次连接各点。
新知探究
y=
4
x
1
2
1
2
-
4
3
1
2
4
3
-
1
2
-
注意要点
1.列表时,自变量的值可以选取一些互为相反数
的值这样既可简化计算,又便于对称性描点;
2.列表时,应尽量多取一些数值,多描一些点,
这样既可以方便连线,又较准确地表达函数
的变化趋势;
3.连线时,一定要按自变量从小到大的顺序,依
次用平滑的曲线连接,从中体会函数的增减性;
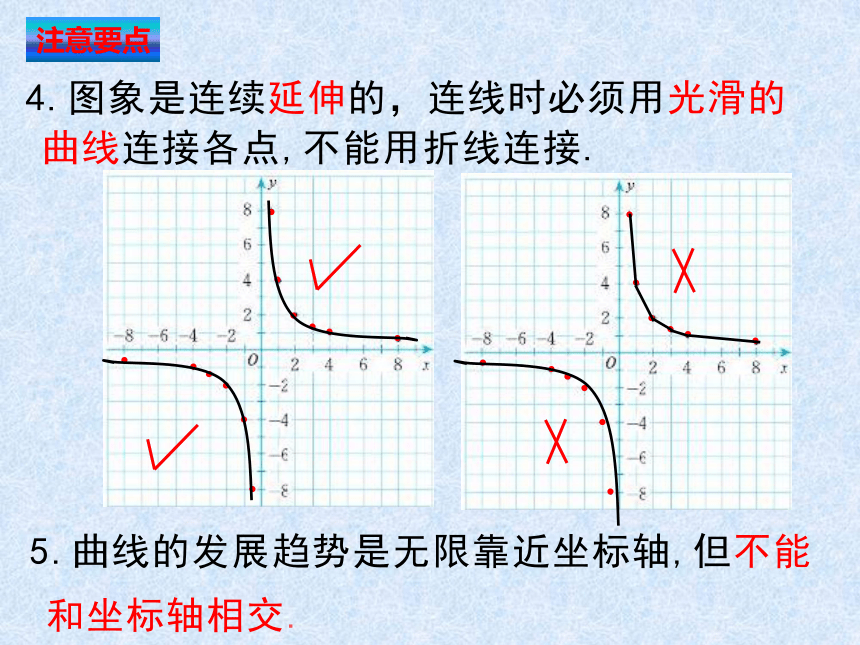
注意要点
5.曲线的发展趋势是无限靠近坐标轴,但不能和坐标轴相交.
4.图象是连续延伸的,连线时必须用光滑的曲线连接各点,不能用折线连接.
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
Ⅰ、我们尝试画 的图像。
(1)列表:
(2)描点:
(3)连线:
用光滑的曲线
顺次连接各点。
y=
-4
x
新知探究
x … …
y … …
-8
-4
-3
-2
-1
1
2
3
4
8
1
2
4
8
-8
-4
-2
-1
1
2
1
2
-
1
2
4
3
-
1
2
-
4
3
新知探究
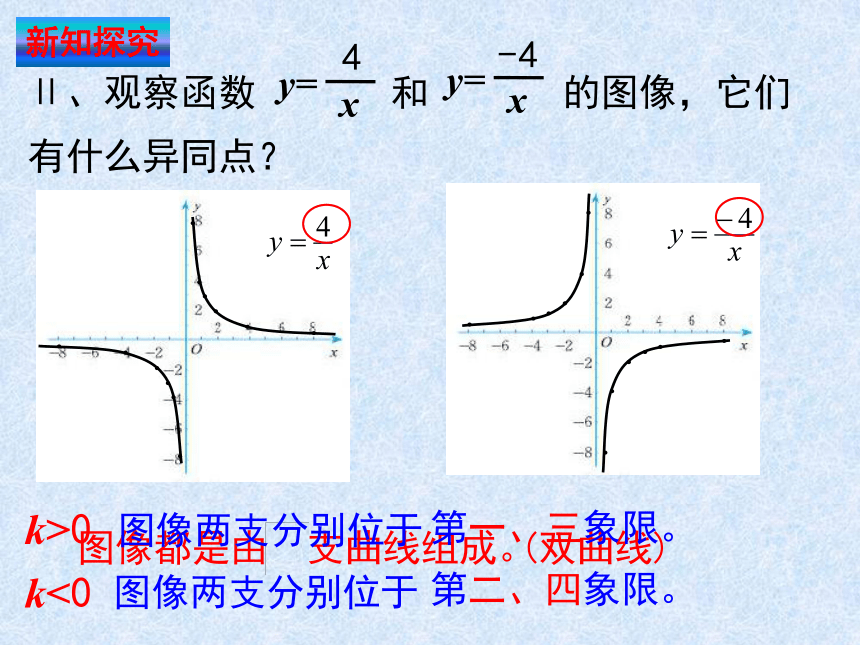
Ⅱ、观察函数 和 的图像,它们有什么异同点?
图像都是由两支曲线组成。
y=
4
x
y=
-4
x
(双曲线)
图像两支分别位于
图像两支分别位于
k>0
k<0
第一、三象限。
第二、四象限。
新知归纳
形状:
位置:
第一、三象限
第二、四象限
y=
k
x
因此称反比例函数 的图象为双曲线
y=
k
x
反比例函数 的图象由两支曲线组成,
当k<0时,两支曲线分别位于_____________内.
当k>0时,两支曲线分别位于_____________内;
由k决定:
反比例函数的图像
新知探究
y
x
o
观察反比例函数的图像
从对称的角度看,
反比例函数
对称中心是_______
是中心对称图形,
你有什么发现?
反比例函数
它有两条对称轴。
是轴对称图形,
原点O
新知探究
例:如图所示的曲线是函数 (m为常数)图象的一支.
(1)求常数m的取值范围;
(2)若该函数的图象与正比例函数y=2x的图象在第一象限的交点为A(2,n),求点A的坐标及反比例函数的解析式.
解(1):
y=
m-5
x
m-5>0,
由题意可得:
解得:m>5.
新知探究
(2)若该函数的图象与正比例函数y=2x的图象在第一象限的交点为A(2,n),求点A的坐标及反比例函数的解析式.
∴ 点A的坐标为(2,4);
解(2):
∵两个函数的交点为A(2,n),
∴
n=
m-5
2
n=4
解得:
m=13,
n=4
反比例函数的解析式为
y=
8
x
练一练
y
A.
x
y
o
B.
x
o
D.
x
y
o
1.反比例函数y= 的图象大致是( )
x
7
x
y
o
C.
D
练一练
2.已知反比例函数 的图象在第一、三象限内,则m的取值范围是________
3.下列函数中,其图象位于第一、三象限的有_____________; 图象位于二、四象限的有_____.
(1)
(4)
y=
m-2
x
m>2
(3)
(2)
练一练
4.如图,已知直线y=mx与双曲线 的一个交点坐标为(-1,3),则它们的另一个交点坐标是 ( )
A. (1,3) B. (3,1)
C. (1,-3) D. (-1,3)
C
y=
k
x
练一练
5.已知点(-m,n)在反比例函数的图象上,则它的图象也一定经过点__________
(m, -n)
6.已知反比例函数的图象经过点(a ,b ),则它的图象一定经过( )
A(-a,-b) B( a,-b)
C(-a,b) D(0,0)
A
练一练
7.若双曲线 的两个分支分别在第二、四象限,则 k 的取值范围是( )
A. k> B. k<
C. k= D.不存在
y=
2k-1
x
1
2
1
2
1
2
2k-1
<0
B
课堂小结
反比例函数的图象
形状:
双曲线
位置
画法:
当k>0时,两支曲线分别位于第一、三象限内
当k<0时,两支曲线分别位于第二、四象限内
描点法:列表、描点、连线
作业
P154
1,2,
6.2.1 反比例函数的图像与性质(一)
第六章 反比例函数
温故知新
一般地,如果两个变量x,y之间的对应关系可以表示成:
的形式,那么称y是x的反比例函数.
y=
k
x
(k 为常数,k≠0)
反比例函数:
反比例函数表达式的三种常见形式:
y=
k
x
(k 为常数,k≠0)
xy=k
y=k
-1
x
一次函数的图像及性质
温故知新
表达式:
图象形状:
位置:
y=kx+b
直线
一定过_______象限
y随x的增大而_____
一定过_______象限
y随x的增大而_____
单调性:
k>0
k<0
位置:
单调性:
反比例函数呢?
(k,b是常数,k≠0)
一、三
二、四
增大
减小
温故知新
如何画函数的图象?
描点法:
列表
描点
连线
Ⅰ、我们尝试画 的图像。
(1)列表:
x … …
y … …
(2)描点:
(3)连线:
用光滑的曲线
-8
-4
-3
-2
-1
1
2
3
4
8
-1
-2
-4
-8
8
4
2
1
·
·
·
·
·
·
·
·
·
·
·
·
顺次连接各点。
新知探究
y=
4
x
1
2
1
2
-
4
3
1
2
4
3
-
1
2
-
注意要点
1.列表时,自变量的值可以选取一些互为相反数
的值这样既可简化计算,又便于对称性描点;
2.列表时,应尽量多取一些数值,多描一些点,
这样既可以方便连线,又较准确地表达函数
的变化趋势;
3.连线时,一定要按自变量从小到大的顺序,依
次用平滑的曲线连接,从中体会函数的增减性;
注意要点
5.曲线的发展趋势是无限靠近坐标轴,但不能和坐标轴相交.
4.图象是连续延伸的,连线时必须用光滑的曲线连接各点,不能用折线连接.
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
Ⅰ、我们尝试画 的图像。
(1)列表:
(2)描点:
(3)连线:
用光滑的曲线
顺次连接各点。
y=
-4
x
新知探究
x … …
y … …
-8
-4
-3
-2
-1
1
2
3
4
8
1
2
4
8
-8
-4
-2
-1
1
2
1
2
-
1
2
4
3
-
1
2
-
4
3
新知探究
Ⅱ、观察函数 和 的图像,它们有什么异同点?
图像都是由两支曲线组成。
y=
4
x
y=
-4
x
(双曲线)
图像两支分别位于
图像两支分别位于
k>0
k<0
第一、三象限。
第二、四象限。
新知归纳
形状:
位置:
第一、三象限
第二、四象限
y=
k
x
因此称反比例函数 的图象为双曲线
y=
k
x
反比例函数 的图象由两支曲线组成,
当k<0时,两支曲线分别位于_____________内.
当k>0时,两支曲线分别位于_____________内;
由k决定:
反比例函数的图像
新知探究
y
x
o
观察反比例函数的图像
从对称的角度看,
反比例函数
对称中心是_______
是中心对称图形,
你有什么发现?
反比例函数
它有两条对称轴。
是轴对称图形,
原点O
新知探究
例:如图所示的曲线是函数 (m为常数)图象的一支.
(1)求常数m的取值范围;
(2)若该函数的图象与正比例函数y=2x的图象在第一象限的交点为A(2,n),求点A的坐标及反比例函数的解析式.
解(1):
y=
m-5
x
m-5>0,
由题意可得:
解得:m>5.
新知探究
(2)若该函数的图象与正比例函数y=2x的图象在第一象限的交点为A(2,n),求点A的坐标及反比例函数的解析式.
∴ 点A的坐标为(2,4);
解(2):
∵两个函数的交点为A(2,n),
∴
n=
m-5
2
n=4
解得:
m=13,
n=4
反比例函数的解析式为
y=
8
x
练一练
y
A.
x
y
o
B.
x
o
D.
x
y
o
1.反比例函数y= 的图象大致是( )
x
7
x
y
o
C.
D
练一练
2.已知反比例函数 的图象在第一、三象限内,则m的取值范围是________
3.下列函数中,其图象位于第一、三象限的有_____________; 图象位于二、四象限的有_____.
(1)
(4)
y=
m-2
x
m>2
(3)
(2)
练一练
4.如图,已知直线y=mx与双曲线 的一个交点坐标为(-1,3),则它们的另一个交点坐标是 ( )
A. (1,3) B. (3,1)
C. (1,-3) D. (-1,3)
C
y=
k
x
练一练
5.已知点(-m,n)在反比例函数的图象上,则它的图象也一定经过点__________
(m, -n)
6.已知反比例函数的图象经过点(a ,b ),则它的图象一定经过( )
A(-a,-b) B( a,-b)
C(-a,b) D(0,0)
A
练一练
7.若双曲线 的两个分支分别在第二、四象限,则 k 的取值范围是( )
A. k> B. k<
C. k= D.不存在
y=
2k-1
x
1
2
1
2
1
2
2k-1
<0
B
课堂小结
反比例函数的图象
形状:
双曲线
位置
画法:
当k>0时,两支曲线分别位于第一、三象限内
当k<0时,两支曲线分别位于第二、四象限内
描点法:列表、描点、连线
作业
P154
1,2,
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
