北师版八年级下册数学 第三章图形的平移与旋转达标检测卷(word版含答案)
文档属性
| 名称 | 北师版八年级下册数学 第三章图形的平移与旋转达标检测卷(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 391.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-19 06:42:40 | ||
图片预览




文档简介
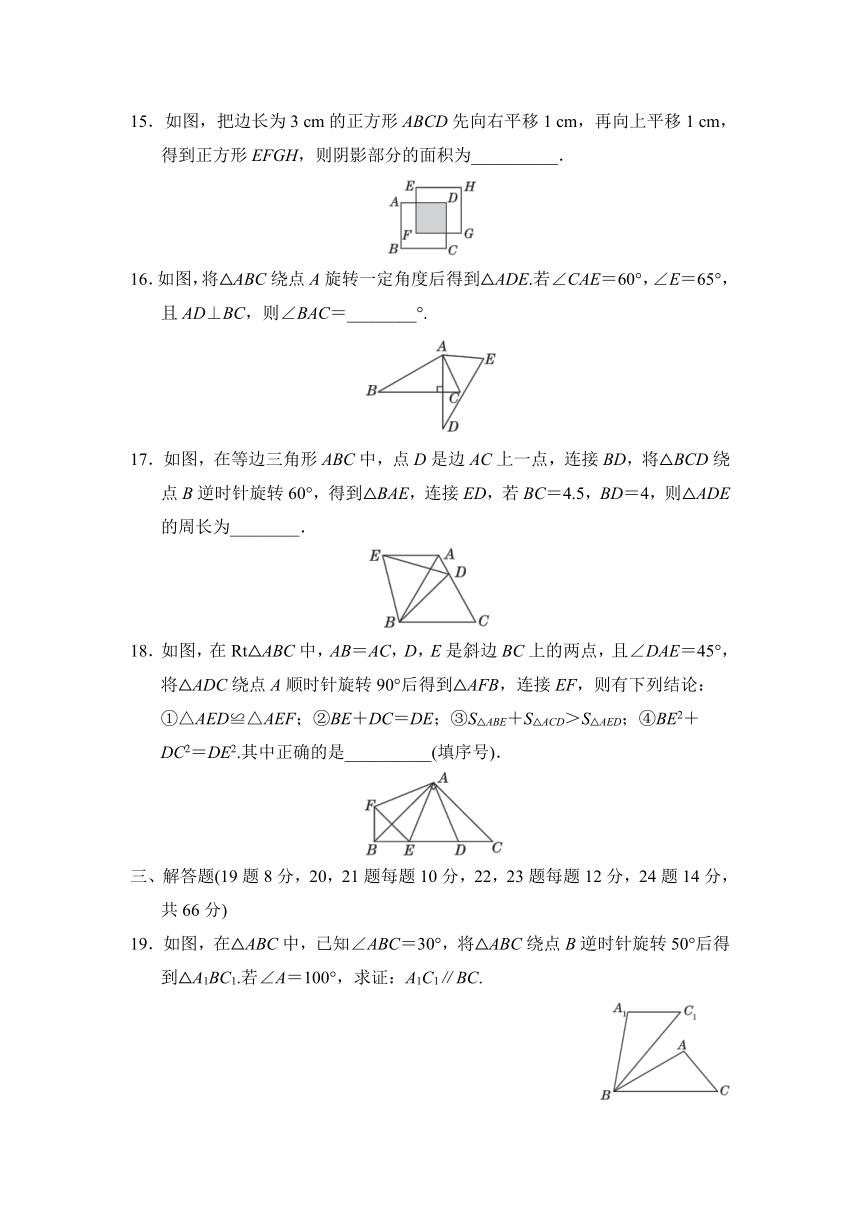
第三章达标检测卷
一、选择题(每题3分,共30分)
1.在平面直角坐标系中,将点A(4,5)向左平移2个单位长度,所得到的点的坐标为( )
A.(2,5) B.(6,5) C.(4,7) D.(2,3)
2.【教材P83随堂练习T1变式】下列图形中,既是轴对称图形又是中心对称图形的是( )
3.【教材P76想一想变式】下列四个图案中,不能由1号图形平移得到2号图形的是( )
4.【教材P89复习题T13变式】如图,在平面直角坐标系中,△ABC绕旋转中心顺时针旋转90°后得到△A′B′C′,则其旋转中心的坐标是( )
A.(1.5,1.5)
B.(1,0)
C.(1,-1)
D.(1.5,-0.5)
5.【教材P90复习题T21变式】如图,在Rt△ABO中,∠ABO=90°,OA=2,
AB=1,把Rt△ABO绕着原点逆时针旋转90°,得到△A′B′O,那么点A′的坐标为( )
A.(-,1)
B.(-2,)
C.(-1,)
D.(-,2)
6.如图,将△ABC沿直线AB向右平移后到达△BDE的位置,连接CD,CE,若△ACD的面积为10,则△BCE的面积为( )
A.5
B.6
C.10
D.4
7.【教材P74习题T3变式】如图,已知点A,B的坐标分别为(3,0),(0,4),将线段AB平移到CD的位置,若点A的对应点C的坐标为(4,2),则点B的对应点D的坐标为( )
A.(1,6)
B.(2,5)
C.(6,1)
D.(4,6)
8.如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )
A.55°
B.60°
C.65°
D.70°
9.如图,把Rt△ABC放在平面直角坐标系内,其中∠CAB=90°,BC=5,点A,B的坐标分别为(1,0),(4,0).将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC平移的距离为( )
A.4
B.5
C.6
D.8
10.如图,8×8的方格纸上的两条对称轴EF,MN相交于中心点O,对△ABC分别作下列变换:
①先以点A为旋转中心顺时针旋转90°,再向右平移
4格、向上平移4格;
②先以点O为对称中心作中心对称图形,再以点A的对应点为旋转中心逆时针旋转90°;
③先以直线MN为对称轴作轴对称图形,然后向上平移4格,再以点A的对应点为旋转中心顺时针旋转90°.
其中,能将△ABC变换成△PQR的是( )
A.①② B.①③ C.②③ D.①②③
二、填空题(每题3分,共24分)
11.如图,每个小正方形的边长都是1,点A,B,C,D,O都是小正方形的顶点.若△COD是由△AOB绕点O按顺时针方向旋转 α(0°<α<360°)得到的,则α=________.
12.在平面直角坐标系中,将点P(-2,1)先向右平移3个单位长度,再向上平移4个单位长度,得到点P′,则点P′的坐标是__________.
13.在平面直角坐标系中,点(a,5)关于原点对称的点的坐标是(1,b+1),则
a+b=________.
14.如图,△ABC的顶点分别为A(3,6),B(1,3),C(4,2).若将△ABC绕点B顺时针旋转90°,得到△A′BC′,则点A的对应点A′的坐标为__________.
15.如图,把边长为3 cm的正方形ABCD先向右平移1 cm,再向上平移1 cm,得到正方形EFGH,则阴影部分的面积为__________.
16.如图,将△ABC绕点A旋转一定角度后得到△ADE.若∠CAE=60°,∠E=65°,且AD⊥BC,则∠BAC=________°.
17.如图,在等边三角形ABC中,点D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=4.5,BD=4,则△ADE的周长为________.
18.如图,在Rt△ABC中,AB=AC,D,E是斜边BC上的两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后得到△AFB,连接EF,则有下列结论:
①△AED≌△AEF;②BE+DC=DE;③S△ABE+S△ACD>S△AED;④BE2+
DC2=DE2.其中正确的是__________(填序号).
三、解答题(19题8分,20,21题每题10分,22,23题每题12分,24题14分,共66分)
19.如图,在△ABC中,已知∠ABC=30°,将△ABC绕点B逆时针旋转50°后得到△A1BC1.若∠A=100°,求证:A1C1∥BC.
20.【教材P77习题T1变式】如图,△ABC是等边三角形,△ABD按顺时针方向旋转后能与△CBD′重合.
(1)旋转中心是________,旋转角是________°;
(2)连接DD′,求证:△BDD′为等边三角形.
21.如图,在Rt△ABC中,∠ACB=90°,AC=4 cm,BC=3 cm,△ABC沿AB方向平移至△DEF,若AE=8 cm,BD=2 cm.求:
(1)△ABC沿AB方向平移的距离;
(2)四边形AEFC的周长.
22.如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点为网格线的交点).
(1)将△ABC先向下平移3个单位长度,再向右平移4个单位长度得到△A1B1C1,画出平移后的图形;
(2)将△ABC绕点A1顺时针旋转90°后得到△A2B2C2,画出旋转后的图形;
(3)借助网格,利用无刻度直尺画出△A1B1C1的中线A1D1(画图中要体现找关键点的方法).
23.如图①,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.
操作发现:如图②,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,
(1)猜想线段DE与AC的位置关系是__________,并加以证明;
(2)设△BDC的面积为S1,△AEC的面积为S2,则S1与S2的数量关系是__________,并加以证明.
24.如图①,在△ABC中,∠A=90°,AB=AC=+1,点D,E分别在边AB,AC上,且AD=AE=1,连接DE.现将△ADE绕点A顺时针方向旋转,旋转角为α(0°<α<360°),如图②,连接CE,BD,CD.
(1)当0°<α<180°时,求证:CE=BD;
(2)如图③,当α=90°时,延长CE交BD于点F,求证:CF垂直平分BD;
(3)在旋转过程中,求△BCD的面积的最大值,并写出此时旋转角α的度数.
答案
一、1.A 2.B 3.D 4.C 5.C 6.A
7.A 8.C 9.A 10.D
二、11.90° 12.(1,5) 13.-7 14.(4,1)
15.4 cm2 16.85 17.8.5
18.①③④ 点拨:由旋转的性质知AF=AD,BF=CD,∠FBA=∠DCA,
∠FAB=∠DAC,∠FAD=∠BAC=90°,∴∠FAE=∠EAD=45°.
又∵AE=AE,∴△AED≌△AEF.∴DE=EF.
∵∠EBF=∠FBA+∠ABE=∠ACD+∠ABE=90°,
∴BE2+BF2=BE2+DC2=EF2=DE2.
又∵S△ABE+S△ACD=S△ABE+S△AFB>S△AED,BE+DC=BE+FB>EF=ED,
∴正确的结论是①③④.
三、19.证明:∵∠ABC=30°,∠A=100°,
∴∠C=50°.
∵将△ABC绕点B逆时针旋转50°后得到△A1BC1,
∴∠CBC1=50°,∠C1=∠C=50°.
∴∠CBC1=∠C1.
∴A1C1∥BC.
20.(1)点B;60
(2)证明:由旋转的性质得BD=BD′.
∵旋转角是60°,∴∠DBD′=60°.
∴△BDD′为等边三角形.
21.解:(1)∵△ABC沿AB方向平移至△DEF,∴AD=BE.
∵AE=8 cm,BD=2 cm,
∴AD==3(cm).
∴△ABC沿AB方向平移的距离是3 cm.
(2)由平移的特征及(1),得CF=AD=3 cm,EF=BC=3 cm.
又∵AE=8 cm,AC=4 cm,
∴四边形AEFC的周长为AE+EF+CF+AC=8+3+3+4=18(cm).
22.解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
(3)如图,线段A1D1即为所求.
23.解:(1)DE∥AC
证明:∵△DEC绕点C旋转,点D恰好落在AB边上,∴AC=CD.
∵在△ABC中,∠ACB=90°,∠B=30°,
∴∠BAC=90°-∠B=90°-30°=60°.
∴△ACD是等边三角形.
∴∠ACD=60°.
∵∠CDE=∠BAC=60°,
∴∠ACD=∠CDE.
∴DE∥AC.
(2)S1=S2
证明:由(1)知△ACD是等边三角形,∴AC=CD=AD.
∵∠B=30°,∠ACB=90°,
∴CD=AC=AD=AB.
∴BD=AD=AC.
根据等边三角形的性质,△ACD的边AC,AD上的高相等,又DE∥AC,
∴易得△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),即S1=S2.
24.(1)证明:易知∠CAE=∠BAD=α.
在△ACE和△ABD中,
∴△ACE≌△ABD(SAS).
∴CE=BD.
(2)证明:由(1)知△ACE≌△ABD,
∴∠ACE=∠ABD.
∵∠ACE+∠AEC=90°,∠AEC=∠FEB,
∴∠ABD+∠FEB=90°.
∴∠EFB=90°.
∴CF⊥BD.
∵AB=AC=+1,AD=AE=1,∠CAB=∠EAD=90°,
∴BC=AB=+2,CD=AC+AD=+2.
∴BD=CD.
又∵CF⊥BD,∴BF=DF.
∴CF垂直平分BD.
(3)解:在△BCD中,边BC的长是定值,则BC边上的高取最大值时△BCD的面积有最大值.
∴当点D在线段BC的垂直平分线上,且在△ABC外部时,△BCD的面积取得最大值.
如图,延长DA交BC于点G,则DG⊥BC.
∵AB=AC=+1,∠CAB=90°,DG⊥BC于点G,
∴AG=BC=,∠GAB=45°.
∴DG=AG+AD=+1=,∠DAB=180°-45°=135°.
∴S△BCD的最大值为BC·DG=×(+2)×=.
此时旋转角α=135°.
一、选择题(每题3分,共30分)
1.在平面直角坐标系中,将点A(4,5)向左平移2个单位长度,所得到的点的坐标为( )
A.(2,5) B.(6,5) C.(4,7) D.(2,3)
2.【教材P83随堂练习T1变式】下列图形中,既是轴对称图形又是中心对称图形的是( )
3.【教材P76想一想变式】下列四个图案中,不能由1号图形平移得到2号图形的是( )
4.【教材P89复习题T13变式】如图,在平面直角坐标系中,△ABC绕旋转中心顺时针旋转90°后得到△A′B′C′,则其旋转中心的坐标是( )
A.(1.5,1.5)
B.(1,0)
C.(1,-1)
D.(1.5,-0.5)
5.【教材P90复习题T21变式】如图,在Rt△ABO中,∠ABO=90°,OA=2,
AB=1,把Rt△ABO绕着原点逆时针旋转90°,得到△A′B′O,那么点A′的坐标为( )
A.(-,1)
B.(-2,)
C.(-1,)
D.(-,2)
6.如图,将△ABC沿直线AB向右平移后到达△BDE的位置,连接CD,CE,若△ACD的面积为10,则△BCE的面积为( )
A.5
B.6
C.10
D.4
7.【教材P74习题T3变式】如图,已知点A,B的坐标分别为(3,0),(0,4),将线段AB平移到CD的位置,若点A的对应点C的坐标为(4,2),则点B的对应点D的坐标为( )
A.(1,6)
B.(2,5)
C.(6,1)
D.(4,6)
8.如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )
A.55°
B.60°
C.65°
D.70°
9.如图,把Rt△ABC放在平面直角坐标系内,其中∠CAB=90°,BC=5,点A,B的坐标分别为(1,0),(4,0).将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC平移的距离为( )
A.4
B.5
C.6
D.8
10.如图,8×8的方格纸上的两条对称轴EF,MN相交于中心点O,对△ABC分别作下列变换:
①先以点A为旋转中心顺时针旋转90°,再向右平移
4格、向上平移4格;
②先以点O为对称中心作中心对称图形,再以点A的对应点为旋转中心逆时针旋转90°;
③先以直线MN为对称轴作轴对称图形,然后向上平移4格,再以点A的对应点为旋转中心顺时针旋转90°.
其中,能将△ABC变换成△PQR的是( )
A.①② B.①③ C.②③ D.①②③
二、填空题(每题3分,共24分)
11.如图,每个小正方形的边长都是1,点A,B,C,D,O都是小正方形的顶点.若△COD是由△AOB绕点O按顺时针方向旋转 α(0°<α<360°)得到的,则α=________.
12.在平面直角坐标系中,将点P(-2,1)先向右平移3个单位长度,再向上平移4个单位长度,得到点P′,则点P′的坐标是__________.
13.在平面直角坐标系中,点(a,5)关于原点对称的点的坐标是(1,b+1),则
a+b=________.
14.如图,△ABC的顶点分别为A(3,6),B(1,3),C(4,2).若将△ABC绕点B顺时针旋转90°,得到△A′BC′,则点A的对应点A′的坐标为__________.
15.如图,把边长为3 cm的正方形ABCD先向右平移1 cm,再向上平移1 cm,得到正方形EFGH,则阴影部分的面积为__________.
16.如图,将△ABC绕点A旋转一定角度后得到△ADE.若∠CAE=60°,∠E=65°,且AD⊥BC,则∠BAC=________°.
17.如图,在等边三角形ABC中,点D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=4.5,BD=4,则△ADE的周长为________.
18.如图,在Rt△ABC中,AB=AC,D,E是斜边BC上的两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后得到△AFB,连接EF,则有下列结论:
①△AED≌△AEF;②BE+DC=DE;③S△ABE+S△ACD>S△AED;④BE2+
DC2=DE2.其中正确的是__________(填序号).
三、解答题(19题8分,20,21题每题10分,22,23题每题12分,24题14分,共66分)
19.如图,在△ABC中,已知∠ABC=30°,将△ABC绕点B逆时针旋转50°后得到△A1BC1.若∠A=100°,求证:A1C1∥BC.
20.【教材P77习题T1变式】如图,△ABC是等边三角形,△ABD按顺时针方向旋转后能与△CBD′重合.
(1)旋转中心是________,旋转角是________°;
(2)连接DD′,求证:△BDD′为等边三角形.
21.如图,在Rt△ABC中,∠ACB=90°,AC=4 cm,BC=3 cm,△ABC沿AB方向平移至△DEF,若AE=8 cm,BD=2 cm.求:
(1)△ABC沿AB方向平移的距离;
(2)四边形AEFC的周长.
22.如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点为网格线的交点).
(1)将△ABC先向下平移3个单位长度,再向右平移4个单位长度得到△A1B1C1,画出平移后的图形;
(2)将△ABC绕点A1顺时针旋转90°后得到△A2B2C2,画出旋转后的图形;
(3)借助网格,利用无刻度直尺画出△A1B1C1的中线A1D1(画图中要体现找关键点的方法).
23.如图①,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.
操作发现:如图②,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,
(1)猜想线段DE与AC的位置关系是__________,并加以证明;
(2)设△BDC的面积为S1,△AEC的面积为S2,则S1与S2的数量关系是__________,并加以证明.
24.如图①,在△ABC中,∠A=90°,AB=AC=+1,点D,E分别在边AB,AC上,且AD=AE=1,连接DE.现将△ADE绕点A顺时针方向旋转,旋转角为α(0°<α<360°),如图②,连接CE,BD,CD.
(1)当0°<α<180°时,求证:CE=BD;
(2)如图③,当α=90°时,延长CE交BD于点F,求证:CF垂直平分BD;
(3)在旋转过程中,求△BCD的面积的最大值,并写出此时旋转角α的度数.
答案
一、1.A 2.B 3.D 4.C 5.C 6.A
7.A 8.C 9.A 10.D
二、11.90° 12.(1,5) 13.-7 14.(4,1)
15.4 cm2 16.85 17.8.5
18.①③④ 点拨:由旋转的性质知AF=AD,BF=CD,∠FBA=∠DCA,
∠FAB=∠DAC,∠FAD=∠BAC=90°,∴∠FAE=∠EAD=45°.
又∵AE=AE,∴△AED≌△AEF.∴DE=EF.
∵∠EBF=∠FBA+∠ABE=∠ACD+∠ABE=90°,
∴BE2+BF2=BE2+DC2=EF2=DE2.
又∵S△ABE+S△ACD=S△ABE+S△AFB>S△AED,BE+DC=BE+FB>EF=ED,
∴正确的结论是①③④.
三、19.证明:∵∠ABC=30°,∠A=100°,
∴∠C=50°.
∵将△ABC绕点B逆时针旋转50°后得到△A1BC1,
∴∠CBC1=50°,∠C1=∠C=50°.
∴∠CBC1=∠C1.
∴A1C1∥BC.
20.(1)点B;60
(2)证明:由旋转的性质得BD=BD′.
∵旋转角是60°,∴∠DBD′=60°.
∴△BDD′为等边三角形.
21.解:(1)∵△ABC沿AB方向平移至△DEF,∴AD=BE.
∵AE=8 cm,BD=2 cm,
∴AD==3(cm).
∴△ABC沿AB方向平移的距离是3 cm.
(2)由平移的特征及(1),得CF=AD=3 cm,EF=BC=3 cm.
又∵AE=8 cm,AC=4 cm,
∴四边形AEFC的周长为AE+EF+CF+AC=8+3+3+4=18(cm).
22.解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
(3)如图,线段A1D1即为所求.
23.解:(1)DE∥AC
证明:∵△DEC绕点C旋转,点D恰好落在AB边上,∴AC=CD.
∵在△ABC中,∠ACB=90°,∠B=30°,
∴∠BAC=90°-∠B=90°-30°=60°.
∴△ACD是等边三角形.
∴∠ACD=60°.
∵∠CDE=∠BAC=60°,
∴∠ACD=∠CDE.
∴DE∥AC.
(2)S1=S2
证明:由(1)知△ACD是等边三角形,∴AC=CD=AD.
∵∠B=30°,∠ACB=90°,
∴CD=AC=AD=AB.
∴BD=AD=AC.
根据等边三角形的性质,△ACD的边AC,AD上的高相等,又DE∥AC,
∴易得△BDC的面积和△AEC的面积相等(等底等高的三角形的面积相等),即S1=S2.
24.(1)证明:易知∠CAE=∠BAD=α.
在△ACE和△ABD中,
∴△ACE≌△ABD(SAS).
∴CE=BD.
(2)证明:由(1)知△ACE≌△ABD,
∴∠ACE=∠ABD.
∵∠ACE+∠AEC=90°,∠AEC=∠FEB,
∴∠ABD+∠FEB=90°.
∴∠EFB=90°.
∴CF⊥BD.
∵AB=AC=+1,AD=AE=1,∠CAB=∠EAD=90°,
∴BC=AB=+2,CD=AC+AD=+2.
∴BD=CD.
又∵CF⊥BD,∴BF=DF.
∴CF垂直平分BD.
(3)解:在△BCD中,边BC的长是定值,则BC边上的高取最大值时△BCD的面积有最大值.
∴当点D在线段BC的垂直平分线上,且在△ABC外部时,△BCD的面积取得最大值.
如图,延长DA交BC于点G,则DG⊥BC.
∵AB=AC=+1,∠CAB=90°,DG⊥BC于点G,
∴AG=BC=,∠GAB=45°.
∴DG=AG+AD=+1=,∠DAB=180°-45°=135°.
∴S△BCD的最大值为BC·DG=×(+2)×=.
此时旋转角α=135°.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
