北师版八年级下册数学 第一章三角形的证明达标检测卷(word版含答案)
文档属性
| 名称 | 北师版八年级下册数学 第一章三角形的证明达标检测卷(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 326.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-19 06:44:30 | ||
图片预览


文档简介
第一章达标检测卷
一、选择题(每题3分,共30分)
1.以下列各组数为边长能组成直角三角形的是( )
A.4,5,6 B.2,3,4
C.11,12,13 D.8,15,17
2.如图,在△ABC中,AB=AC,∠C=72°,BC=,以点B为圆心,BC长为半径画弧,交AC于点D,则线段AD的长为( )
A.2
B.2
C.
D.
3.如图,∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是( )
A.AC=AD
B.AC=BC
C.∠ABC=∠ABD
D.∠BAC=∠BAD
4.【教材P16随堂练习T3改编】下列命题的逆命题是真命题的是( )
A.若a>0,b>0,则a+b>0
B.直角都相等
C.两直线平行,同位角相等
D.若a=b,则|a|=|b|
5.如图,在△ABC中,AC=DC=DB,∠ACB=105°,则∠B的度数为( )
A.15°
B.20°
C.25°
D.40°
6.有A,B,C三个社区(不在同一直线上),现准备修建一座公园,使该公园到三个社区的距离相等,那么公园应建在下列哪个位置上?( )
A.△ABC三条角平分线的交点处
B.△ABC三条中线的交点处
C.△ABC三条高的交点处
D.△ABC三边垂直平分线的交点处
7.如图,D为△ABC内一点,CD平分∠ACB,BE⊥CD,垂足为D,交AC于点E,∠A=∠ABE.若AC=5,BC=3,则BD的长为( )
A.2.5
B.1.5
C.2
D.1
8.【教材P26随堂练习变式】如图,在△ABC中,AB=AC,∠A=120°,BC=6 cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为 ( )
A.4 cm
B.3 cm
C.2 cm
D.1 cm
9.如图,已知∠AOB=30°,P是∠AOB的平分线上一点,CP∥OB,交OA于点C,PD⊥OB,垂足为D,且PC=4,则PD的长等于( )
A.1
B.2
C.4
D.8
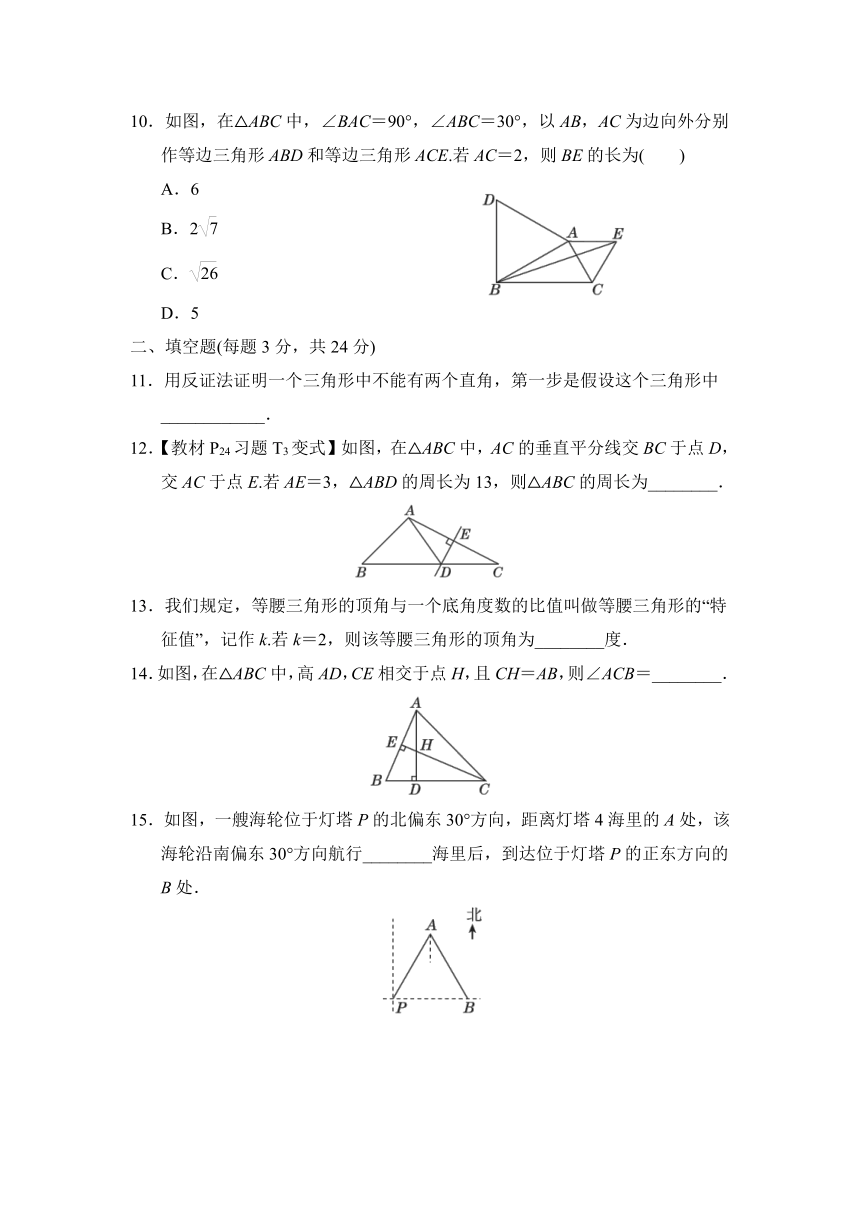
10.如图,在△ABC中,∠BAC=90°,∠ABC=30°,以AB,AC为边向外分别作等边三角形ABD和等边三角形ACE.若AC=2,则BE的长为( )
A.6
B.2
C.
D.5
二、填空题(每题3分,共24分)
11.用反证法证明一个三角形中不能有两个直角,第一步是假设这个三角形中____________.
12.【教材P24习题T3变式】如图,在△ABC中,AC的垂直平分线交BC于点D,交AC于点E.若AE=3,△ABD的周长为13,则△ABC的周长为________.
13.我们规定,等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”,记作k.若k=2,则该等腰三角形的顶角为________度.
14.如图,在△ABC中,高AD,CE相交于点H,且CH=AB,则∠ACB=________.
15.如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔4海里的A处,该海轮沿南偏东30°方向航行________海里后,到达位于灯塔P的正东方向的B处.
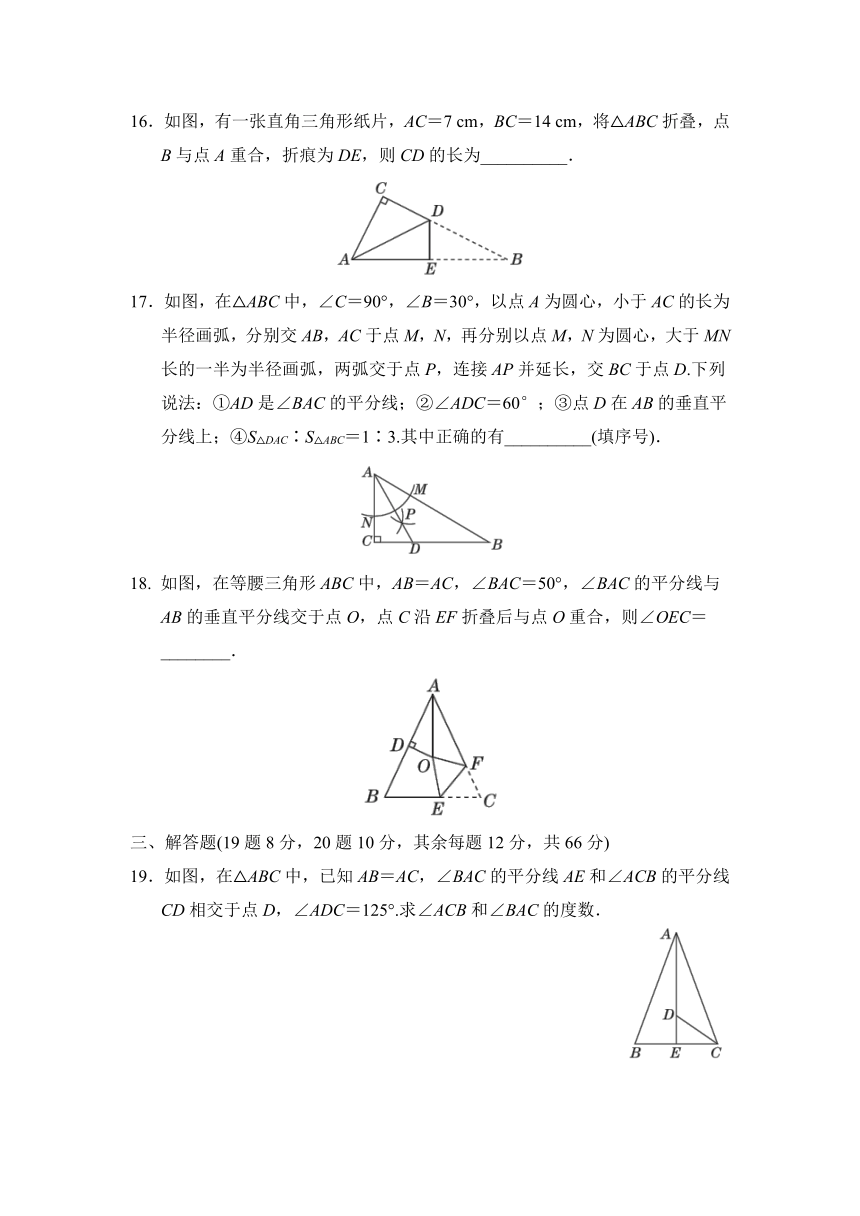
16.如图,有一张直角三角形纸片,AC=7 cm,BC=14 cm,将△ABC折叠,点B与点A重合,折痕为DE,则CD的长为__________.
17.如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,小于AC的长为半径画弧,分别交AB,AC于点M,N,再分别以点M,N为圆心,大于MN长的一半为半径画弧,两弧交于点P,连接AP并延长,交BC于点D.下列说法:①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的垂直平分线上;④S△DAC∶S△ABC=1∶3.其中正确的有__________(填序号).
18. 如图,在等腰三角形ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O,点C沿EF折叠后与点O重合,则∠OEC=________.
三、解答题(19题8分,20题10分,其余每题12分,共66分)
19.如图,在△ABC中,已知AB=AC,∠BAC的平分线AE和∠ACB的平分线CD相交于点D,∠ADC=125°.求∠ACB和∠BAC的度数.
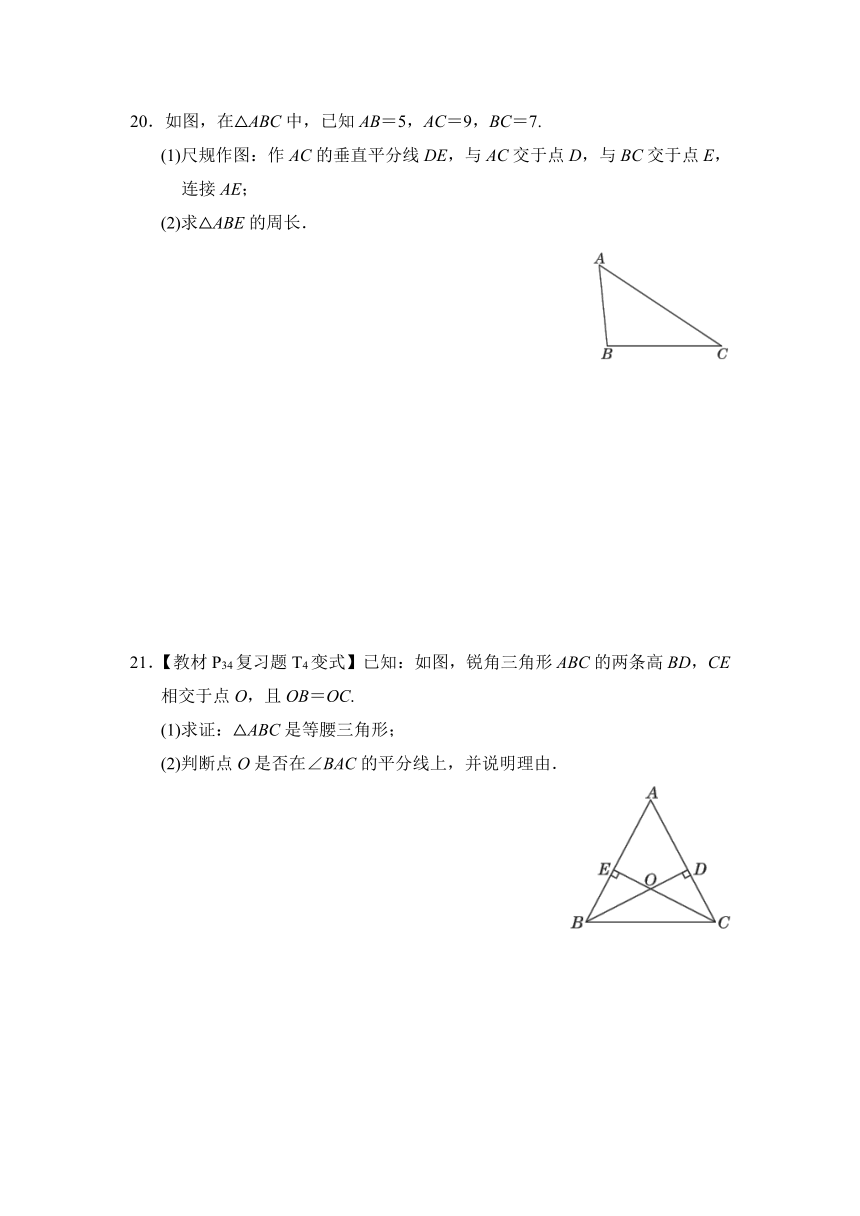
20.如图,在△ABC中,已知AB=5,AC=9,BC=7.
(1)尺规作图:作AC的垂直平分线DE,与AC交于点D,与BC交于点E,连接AE;
(2)求△ABE的周长.
21.【教材P34复习题T4变式】已知:如图,锐角三角形ABC的两条高BD,CE相交于点O,且OB=OC.
(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的平分线上,并说明理由.
22.如图,在△ABC中,AB=AC=5,BC=6,∠ABC与∠ACB的平分线交于点O,过点O作一直线分别交AB,AC于点E,F,且BE=EO.
(1)说明EF与CF的数量关系;
(2)求点O到BC的距离.
23.【教材P31例3拓展】(1)如图①,Rt△ABC中,∠C=90°,∠B=45°,AD是△ABC的角平分线,过点D作DE⊥AB于点E,则AC,CD,AB三条线段之间的数量关系为______________.
(2)若将(1)中的条件“Rt△ABC中,∠C=90°,∠B=45°”改为“△ABC中,∠C=2∠B”,如图②,请问:(1)中的结论是否仍然成立?并证明.
24.定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
举例:如图①,若PA=PB,则点P为△ABC的准外心.
应用:如图②,CD为等边三角形ABC的高,准外心P在高CD上,且
PD=AB.求∠APB的度数.
探究:已知△ABC为直角三角形,斜边BC的长为5,AB=3,准外心P在AC边上.试探究PA的长.
答案
一、1.D 2.C 3.A 4.C 5.C 6.D
7.D 8.C 9.B
10.B 点拨:连接CD.
∵△ABD和△ACE都是等边三角形,
∴AD=AB,AE=AC,∠DAB=∠CAE=60°.
∴∠DAB+∠BAC=∠CAE+∠BAC,即∠DAC=∠BAE.
∴△ABE≌△ADC(SAS).
∴DC=BE.
∵∠ABC=30°,∠ABD=60°,
∴∠DBC=∠ABD+∠ABC=60°+30°=90°.
∵△ABD是等边三角形,AC=2,∠BAC=90°,∠ABC=30°,
∴BC=4,BD=AB=2.
在Rt△DBC中,DC===2,
∴BE=DC=2.
二、11.有两个直角 12.19 13.90
14.45° 15.4 16.5.25 cm
17.①②③④ 18.100°
三、19.解:∵AB=AC,AE平分∠BAC,
∴AE⊥BC.
∵∠ADC=125°,∴∠CDE=55°.
∴∠DCE=90°-∠CDE=35°.
又∵CD平分∠ACB,
∴∠ACB=2∠DCE=70°.
又∵AB=AC,∴∠B=∠ACB=70°.
∴∠BAC=180°-(∠B+∠ACB)=40°.
20.解:(1)如图所示.
(2)∵DE垂直平分AC,∴AE=EC.
∴AB+BE+AE=AB+BE+EC=AB+BC.
∵AB=5,BC=7,
∴AB+BE+AE=5+7=12,
即△ABE的周长为12.
21.(1)证明:∵OB=OC,
∴∠OBC=∠OCB.
∵锐角三角形ABC的两条高BD,CE相交于点O,∴∠BEC=∠BDC=90°.
∴∠BCE+∠ABC=∠DBC+∠ACB=90°.
∴∠ABC=∠ACB.
∴AB=AC,即△ABC是等腰三角形.
(2)解:点O在∠BAC的平分线上.
理由:在△EOB和△DOC中,
∴△EOB≌△DOC(AAS).
∴OE=OD.
又∵OE⊥AE,OD⊥AD,
∴点O在∠BAC的平分线上.
22.解:(1)EF=2CF.理由如下:
如图所示.
∵BE=EO,∴∠1=∠2.
∵在△ABC中,∠ABC与∠ACB的平分线交于点O,∴∠1=∠3,∠4=∠5.
∴∠2=∠3.∴EF∥BC.
∴∠4=∠5=∠6.
∴OF=CF.
∵AB=AC,∴∠ABC=∠ACB.
∵EF∥BC,
∴∠ABC=∠AEF=∠ACB=∠AFE.
∴AE=AF.
∴BE=CF.
∴EF=OE+OF=2CF.
(2)如图,连接AO并延长交BC于点D.
∵在△ABC中,∠ABC与∠ACB的平分线交于点O,AB=AC,
∴AD⊥BC,BD=CD=3.
在Rt△ABD中,AD===4,
∴S△ABC=BC·AD=×6×4=12.
∵点O是△ABC三个内角平分线的交点,
∴点O到三边的距离相等,即为OD的长.
∵S△OBC+S△OAC+S△OAB=S△ABC,
∴BC·OD+AC·OD+AB·OD=12.
∴OD=1.5,即点O到BC的距离是1.5.
23.解:(1)AB=AC+CD
(2)(1)中的结论仍然成立.证明如下:
∵AD是∠CAB的平分线,
∴将△CAD沿AD折叠,点C恰好落在AB边上,记为C′,如图所示.
由折叠的性质知△ACD≌△AC′D,
∴AC=AC′,CD=C′D,∠C=∠1.
∵∠C=2∠B,∴∠1=2∠B.
又∵∠1=∠2+∠B,∴∠2=∠B.
∴C′D=C′B=CD.
∴AB=AC′+BC′=AC+CD.
24.解:应用:若PB=PC,则∠PCB=∠PBC.
∵CD为等边三角形ABC的高,
∴AD=BD,∠PCB=∠ACB=30°.
∴∠PBC=30°.
∵∠ABC=60°,∴∠PBD=30°.
∴PD=BP.
又∵PD2+BD2=PB2,
∴PD=BD=AB,与已知PD=AB矛盾.
∴PB≠PC.
同理可得PA≠PC,∴PA=PB.
由PD=AB,AD=BD,得PD=BD.
∵∠PDB=90°,∴∠DPB=45°.
同理,∠APD=45°.
∴∠APB=90°.
探究:∵AB=3,BC=5,
∴在Rt△ABC中,AC==4.
若PB=PC,设PA=x,则PC=PB=AC-PA=4-x.
在Rt△APB中,AP2+AB2=PB2,
∴x2+32=(4-x)2.
∴x=,即PA=.
若PA=PC,则PA=AC=2.
若PA=PB,则∠PBA=∠A=90°,显然不成立.
综上,PA的长为2或.
一、选择题(每题3分,共30分)
1.以下列各组数为边长能组成直角三角形的是( )
A.4,5,6 B.2,3,4
C.11,12,13 D.8,15,17
2.如图,在△ABC中,AB=AC,∠C=72°,BC=,以点B为圆心,BC长为半径画弧,交AC于点D,则线段AD的长为( )
A.2
B.2
C.
D.
3.如图,∠C=∠D=90°,添加一个条件,可使用“HL”判定Rt△ABC与Rt△ABD全等.以下给出的条件适合的是( )
A.AC=AD
B.AC=BC
C.∠ABC=∠ABD
D.∠BAC=∠BAD
4.【教材P16随堂练习T3改编】下列命题的逆命题是真命题的是( )
A.若a>0,b>0,则a+b>0
B.直角都相等
C.两直线平行,同位角相等
D.若a=b,则|a|=|b|
5.如图,在△ABC中,AC=DC=DB,∠ACB=105°,则∠B的度数为( )
A.15°
B.20°
C.25°
D.40°
6.有A,B,C三个社区(不在同一直线上),现准备修建一座公园,使该公园到三个社区的距离相等,那么公园应建在下列哪个位置上?( )
A.△ABC三条角平分线的交点处
B.△ABC三条中线的交点处
C.△ABC三条高的交点处
D.△ABC三边垂直平分线的交点处
7.如图,D为△ABC内一点,CD平分∠ACB,BE⊥CD,垂足为D,交AC于点E,∠A=∠ABE.若AC=5,BC=3,则BD的长为( )
A.2.5
B.1.5
C.2
D.1
8.【教材P26随堂练习变式】如图,在△ABC中,AB=AC,∠A=120°,BC=6 cm,AB的垂直平分线交BC于点M,交AB于点E,AC的垂直平分线交BC于点N,交AC于点F,则MN的长为 ( )
A.4 cm
B.3 cm
C.2 cm
D.1 cm
9.如图,已知∠AOB=30°,P是∠AOB的平分线上一点,CP∥OB,交OA于点C,PD⊥OB,垂足为D,且PC=4,则PD的长等于( )
A.1
B.2
C.4
D.8
10.如图,在△ABC中,∠BAC=90°,∠ABC=30°,以AB,AC为边向外分别作等边三角形ABD和等边三角形ACE.若AC=2,则BE的长为( )
A.6
B.2
C.
D.5
二、填空题(每题3分,共24分)
11.用反证法证明一个三角形中不能有两个直角,第一步是假设这个三角形中____________.
12.【教材P24习题T3变式】如图,在△ABC中,AC的垂直平分线交BC于点D,交AC于点E.若AE=3,△ABD的周长为13,则△ABC的周长为________.
13.我们规定,等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”,记作k.若k=2,则该等腰三角形的顶角为________度.
14.如图,在△ABC中,高AD,CE相交于点H,且CH=AB,则∠ACB=________.
15.如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔4海里的A处,该海轮沿南偏东30°方向航行________海里后,到达位于灯塔P的正东方向的B处.
16.如图,有一张直角三角形纸片,AC=7 cm,BC=14 cm,将△ABC折叠,点B与点A重合,折痕为DE,则CD的长为__________.
17.如图,在△ABC中,∠C=90°,∠B=30°,以点A为圆心,小于AC的长为半径画弧,分别交AB,AC于点M,N,再分别以点M,N为圆心,大于MN长的一半为半径画弧,两弧交于点P,连接AP并延长,交BC于点D.下列说法:①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的垂直平分线上;④S△DAC∶S△ABC=1∶3.其中正确的有__________(填序号).
18. 如图,在等腰三角形ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O,点C沿EF折叠后与点O重合,则∠OEC=________.
三、解答题(19题8分,20题10分,其余每题12分,共66分)
19.如图,在△ABC中,已知AB=AC,∠BAC的平分线AE和∠ACB的平分线CD相交于点D,∠ADC=125°.求∠ACB和∠BAC的度数.
20.如图,在△ABC中,已知AB=5,AC=9,BC=7.
(1)尺规作图:作AC的垂直平分线DE,与AC交于点D,与BC交于点E,连接AE;
(2)求△ABE的周长.
21.【教材P34复习题T4变式】已知:如图,锐角三角形ABC的两条高BD,CE相交于点O,且OB=OC.
(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的平分线上,并说明理由.
22.如图,在△ABC中,AB=AC=5,BC=6,∠ABC与∠ACB的平分线交于点O,过点O作一直线分别交AB,AC于点E,F,且BE=EO.
(1)说明EF与CF的数量关系;
(2)求点O到BC的距离.
23.【教材P31例3拓展】(1)如图①,Rt△ABC中,∠C=90°,∠B=45°,AD是△ABC的角平分线,过点D作DE⊥AB于点E,则AC,CD,AB三条线段之间的数量关系为______________.
(2)若将(1)中的条件“Rt△ABC中,∠C=90°,∠B=45°”改为“△ABC中,∠C=2∠B”,如图②,请问:(1)中的结论是否仍然成立?并证明.
24.定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
举例:如图①,若PA=PB,则点P为△ABC的准外心.
应用:如图②,CD为等边三角形ABC的高,准外心P在高CD上,且
PD=AB.求∠APB的度数.
探究:已知△ABC为直角三角形,斜边BC的长为5,AB=3,准外心P在AC边上.试探究PA的长.
答案
一、1.D 2.C 3.A 4.C 5.C 6.D
7.D 8.C 9.B
10.B 点拨:连接CD.
∵△ABD和△ACE都是等边三角形,
∴AD=AB,AE=AC,∠DAB=∠CAE=60°.
∴∠DAB+∠BAC=∠CAE+∠BAC,即∠DAC=∠BAE.
∴△ABE≌△ADC(SAS).
∴DC=BE.
∵∠ABC=30°,∠ABD=60°,
∴∠DBC=∠ABD+∠ABC=60°+30°=90°.
∵△ABD是等边三角形,AC=2,∠BAC=90°,∠ABC=30°,
∴BC=4,BD=AB=2.
在Rt△DBC中,DC===2,
∴BE=DC=2.
二、11.有两个直角 12.19 13.90
14.45° 15.4 16.5.25 cm
17.①②③④ 18.100°
三、19.解:∵AB=AC,AE平分∠BAC,
∴AE⊥BC.
∵∠ADC=125°,∴∠CDE=55°.
∴∠DCE=90°-∠CDE=35°.
又∵CD平分∠ACB,
∴∠ACB=2∠DCE=70°.
又∵AB=AC,∴∠B=∠ACB=70°.
∴∠BAC=180°-(∠B+∠ACB)=40°.
20.解:(1)如图所示.
(2)∵DE垂直平分AC,∴AE=EC.
∴AB+BE+AE=AB+BE+EC=AB+BC.
∵AB=5,BC=7,
∴AB+BE+AE=5+7=12,
即△ABE的周长为12.
21.(1)证明:∵OB=OC,
∴∠OBC=∠OCB.
∵锐角三角形ABC的两条高BD,CE相交于点O,∴∠BEC=∠BDC=90°.
∴∠BCE+∠ABC=∠DBC+∠ACB=90°.
∴∠ABC=∠ACB.
∴AB=AC,即△ABC是等腰三角形.
(2)解:点O在∠BAC的平分线上.
理由:在△EOB和△DOC中,
∴△EOB≌△DOC(AAS).
∴OE=OD.
又∵OE⊥AE,OD⊥AD,
∴点O在∠BAC的平分线上.
22.解:(1)EF=2CF.理由如下:
如图所示.
∵BE=EO,∴∠1=∠2.
∵在△ABC中,∠ABC与∠ACB的平分线交于点O,∴∠1=∠3,∠4=∠5.
∴∠2=∠3.∴EF∥BC.
∴∠4=∠5=∠6.
∴OF=CF.
∵AB=AC,∴∠ABC=∠ACB.
∵EF∥BC,
∴∠ABC=∠AEF=∠ACB=∠AFE.
∴AE=AF.
∴BE=CF.
∴EF=OE+OF=2CF.
(2)如图,连接AO并延长交BC于点D.
∵在△ABC中,∠ABC与∠ACB的平分线交于点O,AB=AC,
∴AD⊥BC,BD=CD=3.
在Rt△ABD中,AD===4,
∴S△ABC=BC·AD=×6×4=12.
∵点O是△ABC三个内角平分线的交点,
∴点O到三边的距离相等,即为OD的长.
∵S△OBC+S△OAC+S△OAB=S△ABC,
∴BC·OD+AC·OD+AB·OD=12.
∴OD=1.5,即点O到BC的距离是1.5.
23.解:(1)AB=AC+CD
(2)(1)中的结论仍然成立.证明如下:
∵AD是∠CAB的平分线,
∴将△CAD沿AD折叠,点C恰好落在AB边上,记为C′,如图所示.
由折叠的性质知△ACD≌△AC′D,
∴AC=AC′,CD=C′D,∠C=∠1.
∵∠C=2∠B,∴∠1=2∠B.
又∵∠1=∠2+∠B,∴∠2=∠B.
∴C′D=C′B=CD.
∴AB=AC′+BC′=AC+CD.
24.解:应用:若PB=PC,则∠PCB=∠PBC.
∵CD为等边三角形ABC的高,
∴AD=BD,∠PCB=∠ACB=30°.
∴∠PBC=30°.
∵∠ABC=60°,∴∠PBD=30°.
∴PD=BP.
又∵PD2+BD2=PB2,
∴PD=BD=AB,与已知PD=AB矛盾.
∴PB≠PC.
同理可得PA≠PC,∴PA=PB.
由PD=AB,AD=BD,得PD=BD.
∵∠PDB=90°,∴∠DPB=45°.
同理,∠APD=45°.
∴∠APB=90°.
探究:∵AB=3,BC=5,
∴在Rt△ABC中,AC==4.
若PB=PC,设PA=x,则PC=PB=AC-PA=4-x.
在Rt△APB中,AP2+AB2=PB2,
∴x2+32=(4-x)2.
∴x=,即PA=.
若PA=PC,则PA=AC=2.
若PA=PB,则∠PBA=∠A=90°,显然不成立.
综上,PA的长为2或.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
