冀教版七年级下册数学 第6章 二元一次方程组达标检测卷(word版含答案)
文档属性
| 名称 | 冀教版七年级下册数学 第6章 二元一次方程组达标检测卷(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 127.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-19 06:48:51 | ||
图片预览
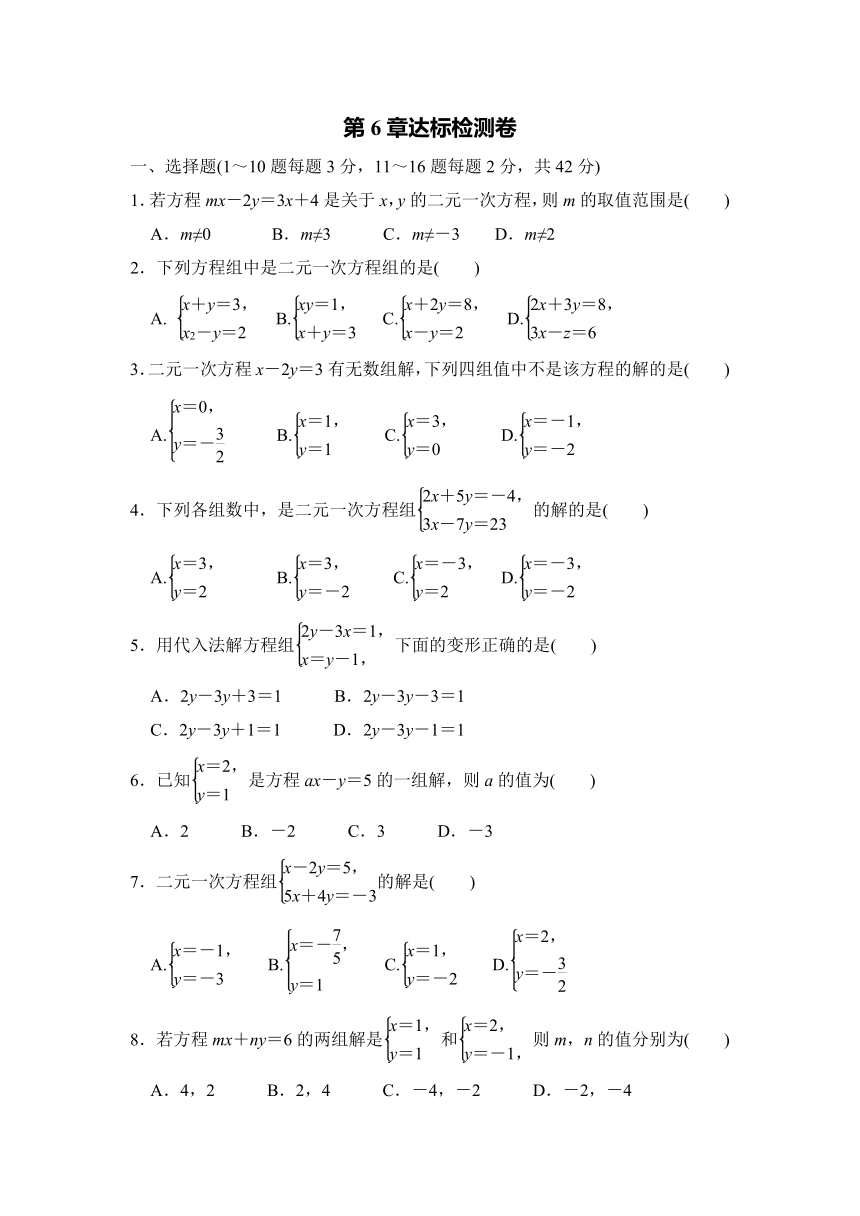




文档简介
第6章达标检测卷
一、选择题(1~10题每题3分,11~16题每题2分,共42分)
1.若方程mx-2y=3x+4是关于x,y的二元一次方程,则m的取值范围是( )
A.m≠0 B.m≠3 C.m≠-3 D.m≠2
2.下列方程组中是二元一次方程组的是( )
A. B. C. D.
3.二元一次方程x-2y=3有无数组解,下列四组值中不是该方程的解的是( )
A. B. C. D.
4.下列各组数中,是二元一次方程组的解的是( )
A. B. C. D.
5.用代入法解方程组下面的变形正确的是( )
A.2y-3y+3=1 B.2y-3y-3=1
C.2y-3y+1=1 D.2y-3y-1=1
6.已知是方程ax-y=5的一组解,则a的值为( )
A.2 B.-2 C.3 D.-3
7.二元一次方程组的解是( )
A. B. C. D.
8.若方程mx+ny=6的两组解是和则m,n的值分别为( )
A.4,2 B.2,4 C.-4,-2 D.-2,-4
9.方程x+y=6的非负整数解有( )
A.6组 B.7组 C.8组 D.无数组
10.关于x,y的二元一次方程组的解是二元一次方程3x-5y=28的一组解,则a的值为( )
A.3 B.2 C.7 D.6
11.我国古代数学著作《孙子算经》有“多人共车”问题:“今有三人共车,二车空;二人共车,九人步.问:人与车各几何?”其大意如下:有若干人要坐车,如果每3人坐一辆车,那么有2辆空车;如果每2人坐一辆车,那么有9人需要步行,问人与车各多少?设共有x人,y辆车,则可列方程组为( )
A. B.
C. D.
12.关于x,y的方程组 的解中x,y的和为6,则k的值为( )
A.14 B.16 C.0 D.-14
13.小亮求得方程组的解为由于不小心,滴上了两滴墨水,刚好遮住了两个数●和★,则●和★表示的数分别为( )
A.5,2 B.8,-2 C.8,2 D.5,4
14.已知方程组和有相同的解,则a,b的值为( )
A. B. C. D.
15.甲、乙两人买了相同数量的信封和相同数量的信笺,甲每发出一封信只用1张信笺,乙每发出一封信用3张信笺.结果甲用掉了所有的信封,但余下50张信笺,而乙用掉了所有的信笺,但余下50个信封,则他们每人买的信笺张数、信封个数分别为( )
A.150,100 B.125,75
C.120,70 D.100,150
16.已知关于x,y的方程组则下列结论正确的是( )
①当a=1时,方程组的解也是方程x+y=2的解;
②当x=y时,a=-;
③不论a取什么值,2x+y的值始终不变.
A.①② B.①③
C.②③ D.①②③
二、填空题(17,19题每题3分,18题4分,共10分)
17.对于方程组若消去z可得含x,y的方程是____________.(含x,y的最简方程)
18.如果|x-2y+1|+(x+y-5)2=0,那么x=________,y=________.
19.《九章算术》中有一道阐述“盈不足术”的问题,原文如下:今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?意思是:几个人一起去购买某物品,如果每人出8钱,则多了3钱;如果每人出7钱,则少了4钱.问有多少人,物品的价值是多少?该问题中物品的价值是________钱.
三、解答题(20,21题每题8分,22~25题每题10分,26题12分,共68分)
20.解方程组:
(1) (2)
(3) (4)
21.已知关于x,y的方程组的解为求m,n的值.
22.如图是小明同学设计的一种计算程序:
―→―→―→
已知当输入的x的值为1时,输出值为1;当输入的x的值为-1时,输出值为-3,则当输入的x的值为-时,求输出值.
23.已知y=ax2+bx+c,当x=-2和x=1时,y的值都是-3,当x=3时,y=7,求a,b,c的值.
24.某县为了改善全县中、小学办学条件,计划集中采购一批电子白板和投影机,已知购买2块电子白板比购买3台投影机多用4 000元,购买4块电子白板和3台投影机共需44 000元,问购买一块电子白板和一台投影机各需多少元?
25.小明和小刚同时解方程组
根据小明和小刚的对话(如图),试求a,b,c的值.
26.电脑中有一种游戏——蜘蛛纸牌,开始游戏前有500分的基本分,游戏规则如下:①操作一次减x分;②每完成一列加y分.有一次小明在玩这种“蜘蛛纸牌”游戏时,随手用表格记录了两个时段的电脑显示:
第一时段 第二时段
完成列数 2 5
分数 634 898
操作次数 66 102
(1)通过列方程组,求x,y的值;
(2)如果小明最终完成此游戏(即完成10列),分数是1 182,问他一共操作了多少次?
答案
一、1.B 2.C 3.B 4.B 5.A
6.C 7.C 8.A
9.B 点拨:注意非负整数包含正整数和零,本题运用枚举法,当x=0时,y=6;当x=1时,y=5;当x=2时,y=4;当x=3时,y=3;当x=4时,y=2;当x=5时,y=1;当x=6时,y=0,故非负整数解有7组.
10.B 11.C 12.A 13.B 14.D
15.A 点拨:设他们每人买了x个信封和y张信笺.
由题意得
解得故选A.
16.C 点拨:①当a=1时,原方程组为
①+②,得x=4,
将x=4代入①,得y=-4,
所以方程组的解为
将所得解代入x+y=2中,不能使等式成立,
所以当a=1时,方程组的解不是方程x+y=2的解,
故①错误;
②
①+②,得x=3+a,
将x=3+a代入①,
得y=-2a-2.
因为x=y,
所以3+a=-2a-2,
所以a=-,
故②正确;
③由②可得方程组的解为
所以2x+y=6+2a-2a-2=4,
所以不论a取什么值,2x+y的值始终不变,
故③正确.
故选C.
二、17.3x-y=3
18.3;2 点拨:由两个非负数的和为0,则这两个非负数必为0,得解方程组从而求得x,y的值.
19.53
三、20.解:(1)方程组整理得:
①×15+②×2,得49x=-294,
解得x=-6.
把x=-6代入②,得y=1.
所以原方程组的解为
(2)
由②得x=9+,③
将③代入①,得3+-=6,
解得y=-9.
将y=-9代入③,得x=.
所以原方程组的解为
(3)令x+y=a,x-y=b,则原方程组变为解这个方程组,得即
解得
(4)
由①+③,得4x-3z=6,④
由①+②×2,得5x+7z=29,⑤
由④和⑤组成方程组
解这个方程组,得
把x=3,z=2代入①,得3-2y+2=9,
解得y=-2.
所以原方程组的解为
21.解:将代入方程组,
得
解得
22.解:根据题意,得
解得
所以,当输入的x的值为-时,输出值为-2.
23.解:将x=-2和y=-3代入y=ax2+bx+c中,
得4a-2b+c=-3.
将x=1和y=-3代入y=ax2+bx+c中,
得a+b+c=-3.
将x=3和y=7代入y=ax2+bx+c中,
得9a+3b+c=7.
可得方程组
解这个方程组,得
24.解:设购买一块电子白板需x元,购买一台投影机需y元,依题意列方程组为
解得
答:购买一块电子白板需8 000元,购买一台投影机需4 000元.
25.解:把分别代入方程组的第1个方程中,
得解得
再把代入方程cx+y=6中,得4c+(-2)=6,解得c=2.
故a=5,b=-3,c=2.
26.解:(1)依题意得
解得
(2)设他一共操作了a次,则10×100-a×1=1 182-500,
解得a=318.
答:他一共操作了318次.
一、选择题(1~10题每题3分,11~16题每题2分,共42分)
1.若方程mx-2y=3x+4是关于x,y的二元一次方程,则m的取值范围是( )
A.m≠0 B.m≠3 C.m≠-3 D.m≠2
2.下列方程组中是二元一次方程组的是( )
A. B. C. D.
3.二元一次方程x-2y=3有无数组解,下列四组值中不是该方程的解的是( )
A. B. C. D.
4.下列各组数中,是二元一次方程组的解的是( )
A. B. C. D.
5.用代入法解方程组下面的变形正确的是( )
A.2y-3y+3=1 B.2y-3y-3=1
C.2y-3y+1=1 D.2y-3y-1=1
6.已知是方程ax-y=5的一组解,则a的值为( )
A.2 B.-2 C.3 D.-3
7.二元一次方程组的解是( )
A. B. C. D.
8.若方程mx+ny=6的两组解是和则m,n的值分别为( )
A.4,2 B.2,4 C.-4,-2 D.-2,-4
9.方程x+y=6的非负整数解有( )
A.6组 B.7组 C.8组 D.无数组
10.关于x,y的二元一次方程组的解是二元一次方程3x-5y=28的一组解,则a的值为( )
A.3 B.2 C.7 D.6
11.我国古代数学著作《孙子算经》有“多人共车”问题:“今有三人共车,二车空;二人共车,九人步.问:人与车各几何?”其大意如下:有若干人要坐车,如果每3人坐一辆车,那么有2辆空车;如果每2人坐一辆车,那么有9人需要步行,问人与车各多少?设共有x人,y辆车,则可列方程组为( )
A. B.
C. D.
12.关于x,y的方程组 的解中x,y的和为6,则k的值为( )
A.14 B.16 C.0 D.-14
13.小亮求得方程组的解为由于不小心,滴上了两滴墨水,刚好遮住了两个数●和★,则●和★表示的数分别为( )
A.5,2 B.8,-2 C.8,2 D.5,4
14.已知方程组和有相同的解,则a,b的值为( )
A. B. C. D.
15.甲、乙两人买了相同数量的信封和相同数量的信笺,甲每发出一封信只用1张信笺,乙每发出一封信用3张信笺.结果甲用掉了所有的信封,但余下50张信笺,而乙用掉了所有的信笺,但余下50个信封,则他们每人买的信笺张数、信封个数分别为( )
A.150,100 B.125,75
C.120,70 D.100,150
16.已知关于x,y的方程组则下列结论正确的是( )
①当a=1时,方程组的解也是方程x+y=2的解;
②当x=y时,a=-;
③不论a取什么值,2x+y的值始终不变.
A.①② B.①③
C.②③ D.①②③
二、填空题(17,19题每题3分,18题4分,共10分)
17.对于方程组若消去z可得含x,y的方程是____________.(含x,y的最简方程)
18.如果|x-2y+1|+(x+y-5)2=0,那么x=________,y=________.
19.《九章算术》中有一道阐述“盈不足术”的问题,原文如下:今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?意思是:几个人一起去购买某物品,如果每人出8钱,则多了3钱;如果每人出7钱,则少了4钱.问有多少人,物品的价值是多少?该问题中物品的价值是________钱.
三、解答题(20,21题每题8分,22~25题每题10分,26题12分,共68分)
20.解方程组:
(1) (2)
(3) (4)
21.已知关于x,y的方程组的解为求m,n的值.
22.如图是小明同学设计的一种计算程序:
―→―→―→
已知当输入的x的值为1时,输出值为1;当输入的x的值为-1时,输出值为-3,则当输入的x的值为-时,求输出值.
23.已知y=ax2+bx+c,当x=-2和x=1时,y的值都是-3,当x=3时,y=7,求a,b,c的值.
24.某县为了改善全县中、小学办学条件,计划集中采购一批电子白板和投影机,已知购买2块电子白板比购买3台投影机多用4 000元,购买4块电子白板和3台投影机共需44 000元,问购买一块电子白板和一台投影机各需多少元?
25.小明和小刚同时解方程组
根据小明和小刚的对话(如图),试求a,b,c的值.
26.电脑中有一种游戏——蜘蛛纸牌,开始游戏前有500分的基本分,游戏规则如下:①操作一次减x分;②每完成一列加y分.有一次小明在玩这种“蜘蛛纸牌”游戏时,随手用表格记录了两个时段的电脑显示:
第一时段 第二时段
完成列数 2 5
分数 634 898
操作次数 66 102
(1)通过列方程组,求x,y的值;
(2)如果小明最终完成此游戏(即完成10列),分数是1 182,问他一共操作了多少次?
答案
一、1.B 2.C 3.B 4.B 5.A
6.C 7.C 8.A
9.B 点拨:注意非负整数包含正整数和零,本题运用枚举法,当x=0时,y=6;当x=1时,y=5;当x=2时,y=4;当x=3时,y=3;当x=4时,y=2;当x=5时,y=1;当x=6时,y=0,故非负整数解有7组.
10.B 11.C 12.A 13.B 14.D
15.A 点拨:设他们每人买了x个信封和y张信笺.
由题意得
解得故选A.
16.C 点拨:①当a=1时,原方程组为
①+②,得x=4,
将x=4代入①,得y=-4,
所以方程组的解为
将所得解代入x+y=2中,不能使等式成立,
所以当a=1时,方程组的解不是方程x+y=2的解,
故①错误;
②
①+②,得x=3+a,
将x=3+a代入①,
得y=-2a-2.
因为x=y,
所以3+a=-2a-2,
所以a=-,
故②正确;
③由②可得方程组的解为
所以2x+y=6+2a-2a-2=4,
所以不论a取什么值,2x+y的值始终不变,
故③正确.
故选C.
二、17.3x-y=3
18.3;2 点拨:由两个非负数的和为0,则这两个非负数必为0,得解方程组从而求得x,y的值.
19.53
三、20.解:(1)方程组整理得:
①×15+②×2,得49x=-294,
解得x=-6.
把x=-6代入②,得y=1.
所以原方程组的解为
(2)
由②得x=9+,③
将③代入①,得3+-=6,
解得y=-9.
将y=-9代入③,得x=.
所以原方程组的解为
(3)令x+y=a,x-y=b,则原方程组变为解这个方程组,得即
解得
(4)
由①+③,得4x-3z=6,④
由①+②×2,得5x+7z=29,⑤
由④和⑤组成方程组
解这个方程组,得
把x=3,z=2代入①,得3-2y+2=9,
解得y=-2.
所以原方程组的解为
21.解:将代入方程组,
得
解得
22.解:根据题意,得
解得
所以,当输入的x的值为-时,输出值为-2.
23.解:将x=-2和y=-3代入y=ax2+bx+c中,
得4a-2b+c=-3.
将x=1和y=-3代入y=ax2+bx+c中,
得a+b+c=-3.
将x=3和y=7代入y=ax2+bx+c中,
得9a+3b+c=7.
可得方程组
解这个方程组,得
24.解:设购买一块电子白板需x元,购买一台投影机需y元,依题意列方程组为
解得
答:购买一块电子白板需8 000元,购买一台投影机需4 000元.
25.解:把分别代入方程组的第1个方程中,
得解得
再把代入方程cx+y=6中,得4c+(-2)=6,解得c=2.
故a=5,b=-3,c=2.
26.解:(1)依题意得
解得
(2)设他一共操作了a次,则10×100-a×1=1 182-500,
解得a=318.
答:他一共操作了318次.
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
