2021-2022学年北师大版九年级数学下册1.6利用三角函数测高同步达标测试(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册1.6利用三角函数测高同步达标测试(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 344.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 11:17:21 | ||
图片预览


文档简介
2021-2022学年北师大版九年级数学下册《1.6利用三角函数测高》同步达标测试(附答案)
一.选择题(共7小题,满分35分)
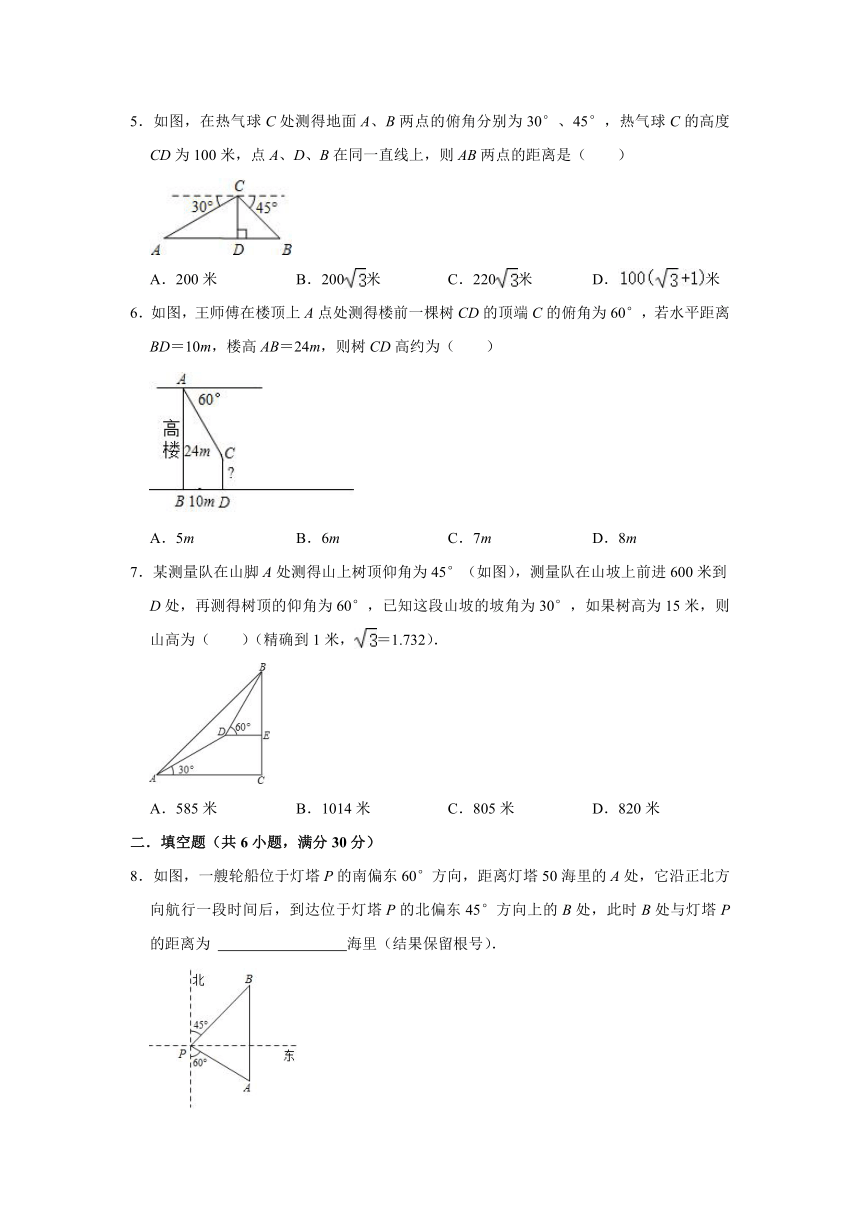
1.如图,要得到从点D观测点A的俯角,可以测量( )
A.∠DAB B.∠DCE C.∠DCA D.∠ADC
2.如图,小明在学校门口的点C处测得树的顶端A仰角为α,同时测得AC=15m,则树的高度AB为( )
A. B.15tanαm C. D.15sinαm
3.如图,一艘海轮位于灯塔P的南偏东37°方向,距离灯塔40海里的A处,它沿正北方向航行一段时间后,到达位于灯塔的正东方向上的B处,这时,B处与灯塔P的距离PB的长可以表示为( )
A.40海里 B.40sin37°海里
C.40cos37°海里 D.40tan37°海里
4.如图,某建筑物的顶部有一块标识牌CD,小明在斜坡上B处测得标识牌顶部C的仰角为45°,沿斜坡走下来在地面A处测得标识牌底部D的仰角为60°,已知斜坡AB的坡角为30°,AB=AE=10米.则标识牌CD的高度是( )米.
A.15﹣5 B.20﹣10 C.10﹣5 D.5﹣5
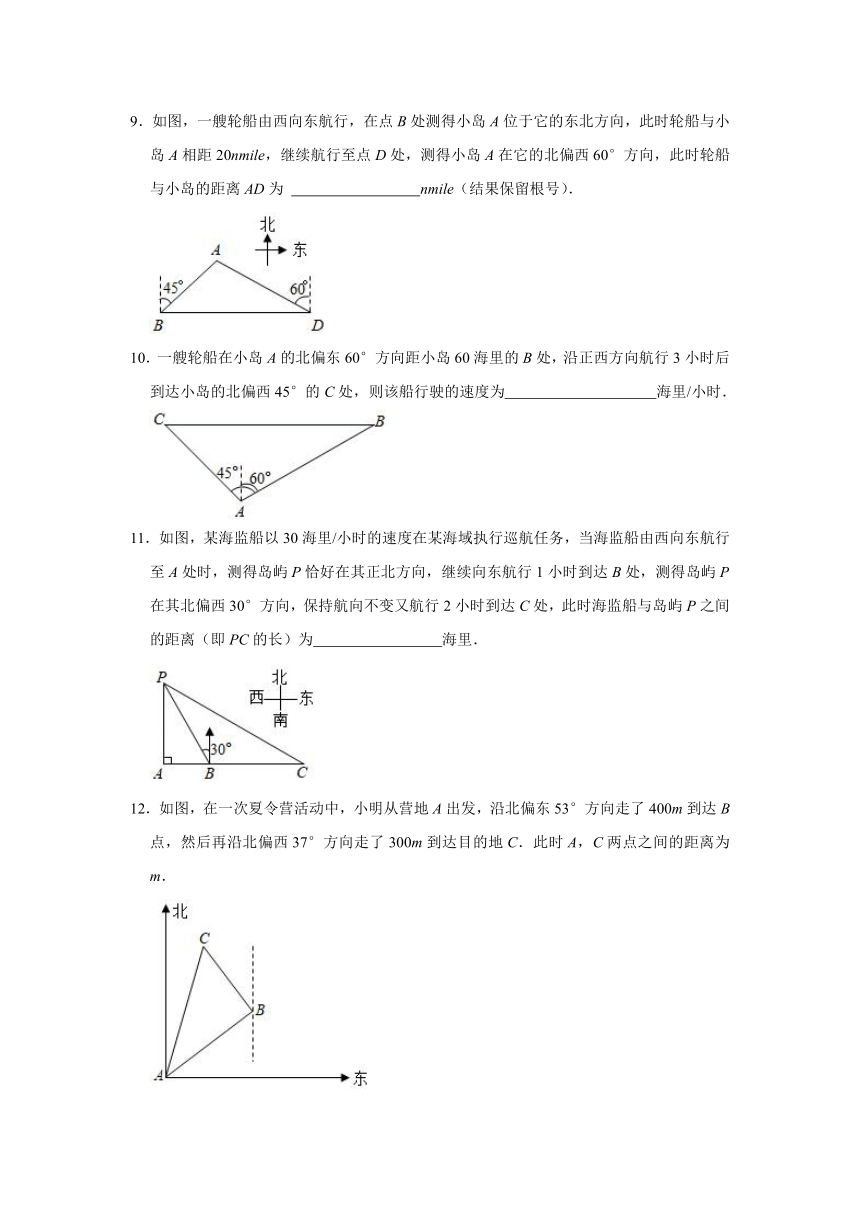
5.如图,在热气球C处测得地面A、B两点的俯角分别为30°、45°,热气球C的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是( )
A.200米 B.200米 C.220米 D.米
6.如图,王师傅在楼顶上A点处测得楼前一棵树CD的顶端C的俯角为60°,若水平距离BD=10m,楼高AB=24m,则树CD高约为( )
A.5m B.6m C.7m D.8m
7.某测量队在山脚A处测得山上树顶仰角为45°(如图),测量队在山坡上前进600米到D处,再测得树顶的仰角为60°,已知这段山坡的坡角为30°,如果树高为15米,则山高为( )(精确到1米,=1.732).
A.585米 B.1014米 C.805米 D.820米
二.填空题(共6小题,满分30分)
8.如图,一艘轮船位于灯塔P的南偏东60°方向,距离灯塔50海里的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东45°方向上的B处,此时B处与灯塔P的距离为 海里(结果保留根号).
9.如图,一艘轮船由西向东航行,在点B处测得小岛A位于它的东北方向,此时轮船与小岛A相距20nmile,继续航行至点D处,测得小岛A在它的北偏西60°方向,此时轮船与小岛的距离AD为 nmile(结果保留根号).
10.一艘轮船在小岛A的北偏东60°方向距小岛60海里的B处,沿正西方向航行3小时后到达小岛的北偏西45°的C处,则该船行驶的速度为 海里/小时.
11.如图,某海监船以30海里/小时的速度在某海域执行巡航任务,当海监船由西向东航行至A处时,测得岛屿P恰好在其正北方向,继续向东航行1小时到达B处,测得岛屿P在其北偏西30°方向,保持航向不变又航行2小时到达C处,此时海监船与岛屿P之间的距离(即PC的长)为 海里.
12.如图,在一次夏令营活动中,小明从营地A出发,沿北偏东53°方向走了400m到达B点,然后再沿北偏西37°方向走了300m到达目的地C.此时A,C两点之间的距离为 m.
13.小明想要测量水面人工岛上两棵小树CD的距离,如图,已知河岸MN∥CD,小明在河岸MN上点A处测量小树C位于北偏东60°方向,然后沿河岸走了20米,到达点B处,此时测得河对岸小树C位于北偏东30°方向,小树D位于东北方向,则两棵树CD的距离为 米.(结果保留根号)
三.解答题(共8小题,满分55分)
14.清代《修武县志》有胜果寺的记载,“康熙五十二年三月十七日,塔顶现青白二气如云,越二日乃止”,此文中的塔即为“胜果寺塔”.是修武作为“千年古县”的标志性古建筑,为了测量塔的高度,某校数学兴趣小组的两名同学采用了如下方式进行测量.如图,小明站在A处,眼睛E距离地面的高度为1.85m,测得塔顶C的仰角为45°,小红站在距离小明10m的D处,眼睛F距离地面的高度为1.5m,测得塔顶C的仰角为60°,已知A,D,塔底B在同一水平面上,由此即可求出塔高BC.你知道是怎么求的吗?请写出解题过程.(结果精确到1m.参考数据:=1.732)
15.如图,一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东39°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(结果精确到0.01小时,sin39°≈0.629,cos39°≈0.777,tan39°≈0.810)
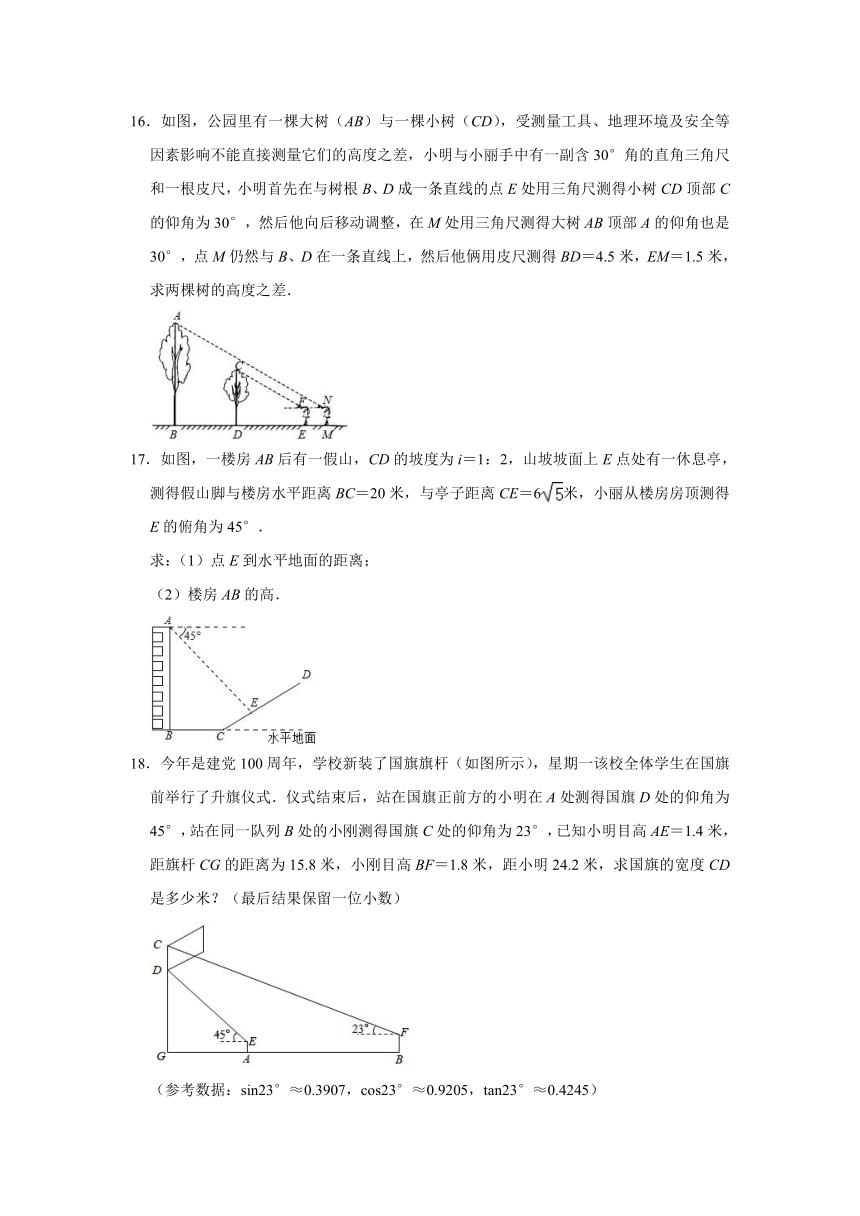
16.如图,公园里有一棵大树(AB)与一棵小树(CD),受测量工具、地理环境及安全等因素影响不能直接测量它们的高度之差,小明与小丽手中有一副含30°角的直角三角尺和一根皮尺,小明首先在与树根B、D成一条直线的点E处用三角尺测得小树CD顶部C的仰角为30°,然后他向后移动调整,在M处用三角尺测得大树AB顶部A的仰角也是30°,点M仍然与B、D在一条直线上,然后他俩用皮尺测得BD=4.5米,EM=1.5米,求两棵树的高度之差.
17.如图,一楼房AB后有一假山,CD的坡度为i=1:2,山坡坡面上E点处有一休息亭,测得假山脚与楼房水平距离BC=20米,与亭子距离CE=6米,小丽从楼房房顶测得E的俯角为45°.
求:(1)点E到水平地面的距离;
(2)楼房AB的高.
18.今年是建党100周年,学校新装了国旗旗杆(如图所示),星期一该校全体学生在国旗前举行了升旗仪式.仪式结束后,站在国旗正前方的小明在A处测得国旗D处的仰角为45°,站在同一队列B处的小刚测得国旗C处的仰角为23°,已知小明目高AE=1.4米,距旗杆CG的距离为15.8米,小刚目高BF=1.8米,距小明24.2米,求国旗的宽度CD是多少米?(最后结果保留一位小数)
(参考数据:sin23°≈0.3907,cos23°≈0.9205,tan23°≈0.4245)
19.小张早起在一条东西走向的笔直马路上晨跑,他在A处时,D处学校和E处图书馆都在他的东北方向,当小张沿正东方向跑了600m到达B处时,E处图书馆在他的北偏东15°方向,然后他由B处继续向正东方向跑600m到达C处,此时D处学校在他的北偏西63.4°方向,求D处学校和E处图书馆之间的距离.(结果保留整数)
(参考数据:sin63.4°≈0.9,cos63.4°≈0.4,tan63.4°≈2.0,≈1.4,≈1.7,≈2.4)
20.如图,A,B是海面上位于东西方向的两个观测点,有一艘海轮在C点处遇险发出求救信号,此时测得C点位于观测点A的北偏东45°方向上,同时位于观测点B的北偏西60°方向上,且测得C点与观测点A的距离为25海里.
(1)求观测点B与C点之间的距离;
(2)有一艘救援船位于观测点B的正南方向且与观测点B相距30海里的D点处,在接到海轮的求救信号后立即前往营救,其航行速度为42海里/小时,求救援船到达C点需要的最少时间.
21.如图,某地政府为解决当地农户网络销售农特产品物流不畅问题,计划打通一条东西方向的隧道AB.无人机从点A的正上方点C,沿正东方向以8m/s的速度飞行15s到达点D,测得A的俯角为60°,然后以同样的速度沿正东方向又飞行50s到达点E,测得点B的俯角为37°.
(1)求无人机的高度AC(结果保留根号);
(2)求AB的长度(结果精确到1m).
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,≈1.73)
参考答案
一.选择题(共7小题,满分35分)
1.解:从点D观测点A的俯角即从点A观测点D的仰角,即∠DAB.
故选:A.
2.解:在Rt△ABC中,AC=15m,∠ACB=α,sinα=,
∴AB=AC sinα=15sinα(m),
故选:D.
3.解:∵一艘海轮位于灯塔P的南偏东37°方向,
∴∠BAP=37°,
∵AP=40海里,
∴BP=AP sin37°=40sin37°海里;
故选:B.
4.解:过点B作BM⊥EA的延长线于点M,过点B作BN⊥CE于点N,如图所示.
在Rt△ABM中,AB=10米,∠BAM=30°,
∴AM=AB cos∠BAM=5米,BM=AB sin∠BAM=5米.
在Rt△ADE中,AE=10米,∠DAE=60°,
∴DE=AE tan∠DAE=10米.
在Rt△BCN中,BN=AE+AM=(10+5)米,∠CBN=45°,
∴CN=BN tan∠CBN=(10+5)米,
∴CD=CN+EN﹣DE=10+5+5﹣10=(15﹣5)米.
故选:A.
5.解:∵在热气球C处测得地面B点的俯角为45°,
∴BD=CD=100米,
∵在热气球C处测得地面A点的俯角为30°,
∴AC=2×100=200米,
∴AD==100米,
∴AB=AD+BD=100+100=100(1+)米,
故选:D.
6.解:过C作CE⊥AB,交AB于点E,
在Rt△ACE中,∠EAC=30°,CE=10m,
∴AC=2CE=20m,AE==10m,
则CD=EB=AB﹣AE=24﹣10≈7m.
故选:C.
7.解:过点D作DF⊥AC于F.
在直角△ADF中,AF=AD cos30°=300米,DF=AD=300米.
设FC=x,则AC=300+x.
在直角△BDE中,BE=DE=x,则BC=300+x.
在直角△ACB中,∠BAC=45°.
∴这个三角形是等腰直角三角形.
∴AC=BC.
∴300+x=300+x.
解得:x=300.
∴BC=AC=300+300.
∴山高是300+300﹣15=285+300≈805米.
故选:C.
二.填空题(共6小题,满分30分)
8.解:过P作PC⊥AB于C,如图所示:
由题意得:∠APC=30°,∠BPC=45°,PA=50海里,
在Rt△APC中,cos∠APC=,
∴PC=PA cos∠APC=50×=25(海里),
在Rt△PCB中,cos∠BPC=,
∴PB===25(海里),
故答案为:25.
9.解:作AC⊥BD于点C,
由已知可得,∠BAC=45°,∠DAC=60°,AB=20nmile,
∵AC⊥BD,
∴∠ACB=∠ACD=90°,
∴AC=AB cos45°=20×=10(nmile),
∴AD===20(nmile),
故答案为:20.
10.解:如图所示:
设该船行驶的速度为x海里/时,
3小时后到达小岛的北偏西45°的C处,
由题意得:AB=60海里,BC=3x海里,
在直角三角形ABQ中,∠BAQ=60°,
∴∠B=90°﹣60°=30°,
∴AQ=AB=30,BQ=AQ=30,
在直角三角形AQC中,∠CAQ=45°,
∴CQ=AQ=30,
∴BC=30+30=3x,
解得:x=10+10(海里/时).
即该船行驶的速度为(10+10)海里/时;
故答案为:10+10.
11.解:在Rt△PAB中,∠APB=30°,
∴PB=2AB,
由题意得BC=2AB,
∴PB=BC,
∴∠C=∠CPB,
∵∠ABP=∠C+∠CPB=60°,
∴∠C=30°,
∴PC=2PA,
∵PA=AB tan60°,AB=30×1=30(海里),
∴PC=2×30×=60(海里),
故答案为:60.
12.解:如图,由题意得:AB=400m,BC=300m,∠CBD=37°,∠BAF=53°,AF∥DE,
∴∠ABE=∠BAF=53°,
∴∠ABC=180°﹣∠CBD﹣∠ABE=180°﹣37°﹣53°=90°,
∴AC===500(m),
即A,C两点之间的距离为500m,
故答案为:500.
13.解:如图所示,过点C作CE⊥MN于点E,过点D作DF⊥MN于点F,
设BE=a,
在Rt△BCE中,∵∠BCE=30°,
∴CE===a,
在Rt△ACE中,∵∠CAE=30°,AB=20,
∴由tan∠CAE=可得=,
解得a=10,
∴BE=10,DF=CE=10,
在Rt△BDF中,∵∠DBF=45°,
∴BF=DF=10,
∴CD=EF=BF﹣BE=10﹣10(米),
故答案为:(10﹣10).
三.解答题(共8小题,满分55分)
14.解:过E点作EG⊥BC于G,过F点作FH⊥BC于H,
设BC=xm,则CG=(x﹣1.85)m,CH=(x﹣1.5)m,
在Rt△CHF中,FH==,
Rt△CGE中,EG==(x﹣1.85)m,
∵EG﹣FH=10,
∴(x﹣1.85)﹣=10,
解得x≈26.
故塔高BC大约26m高.
15.解:如图,过点C作CD⊥AB交AB延长线于D.
在Rt△ACD中,∵∠ADC=90°,∠CAD=30°,AC=80海里,
∴CD=AC=40海里.
在Rt△CBD中,∵∠CDB=90°,∠BCD=39°,
∴BC==海里,
∴海警船到大事故船C处所需的时间大约为:÷40=≈1.29(小时).
答:海警船到大事故船C处所需的大约时间为1.29小时.
16.解:如图,延长NF交AB于点G,交CD于点H,
根据题意可知:
四边形BGHD,四边形DHFE,四边形FNME是矩形,
∴GH=BD=4.5米,HF=DE,FN=EM=1.5米,
在Rt△ANG中,∠AGN=90°,∠ANG=30°,
∴AG=GN tan∠ANG
=(GH+HF+FN) tan30°
=(4.5+HF+1.5)
=(6+HF)(米),
在Rt△CFH中,∠CHF=90°,∠CFH=30°,
∴CH=HF tan∠CFH
=HF tan30°
=HF,
∴AB﹣CD=(AG+BG)﹣(CH+DH)
=AG﹣CH
=(6+HF)﹣HF
=2 (米).
答:大树AB比小树CD高2米.
17.解:(1)如图,过点E作EF⊥BC的延长线于F,EH⊥AB于点H,
在Rt△CEF中,
∵CD的坡度为i=1:2,CE=6米,
∵i===tan∠ECF,
∴EF=6米,CF=12米,
∴BH=EF=6(米),
(2)∵HE=BF=BC+CF=20+12=32(米),
在Rt△AHE中,∠HAE=45°,
∴AH=HE=32(米),
∴AB=AH+HB=32+6=38(米).
答:楼房AB的高为38米.
18.解:作EM⊥CG于M,FN⊥CG于N,
由题意得GB=AG+AB=15.8+24.2=40(米),
则FN=GB=40米,
在Rt△EDM中,∠DEM=45°,
∴DM=EM=15.8米,
∵MG=AE=1.4米,
∴DG=DM+MG=15.8+1.4=17.2(米),
∵NG=FB=1.8米,
∴DN=17.2﹣1.8=15.4(米),
在Rt△CNF中,∠CFN=23°,
∵tan∠CFN=≈0.4245,
∴CN=0.4245×40≈17.0(米),
∴CD=CN﹣DN=17.0﹣15.4=1.6(米)
故国旗的宽度CD约为1.6米.
19.解:过D作DM⊥AC于M,
设MD=x,
在Rt△MAD中,∠MAD=45°,
∴△ADM是等腰直角三角形,
∴AM=MD=x,
∴AD=x,
在Rt△MCD中,∠MDC=63.4°,
∴MC≈2MD=2x,
∵AC=600+600=1200,
∴x+2x=1200,
解得:x=400,
∴MD=400m,
∴AD=MD=400,
过B作BN⊥AE于N,
∵∠EAB=45°,∠EBC=75°,
∴∠E=30°,
在Rt△ABN中,∠NAB=45°,AB=600,
∴BN=AN=AB=300,
∴DN=AD﹣AN=400﹣300=100,
在Rt△NBE中,∠E=30°,
∴NE=BN=×300=300,
∴DE=NE﹣DN=300﹣100≈580(m),
即D处学校和E处图书馆之间的距离约是580m.
20.解:(1)如图,过点C作CE⊥AB于点E,
根据题意可知:∠ACE=∠CAE=45°,AC=25海里,
∴AE=CE=25(海里),
∵∠CBE=30°,
∴BE=25(海里),
∴BC=2CE=50(海里).
答:观测点B与C点之间的距离为50海里;
(2)如图,作CF⊥DB于点F,
∵CF⊥DB,FB⊥EB,CE⊥AB,
∴四边形CEBF是矩形,
∴FB=CE=25(海里),CF=BE=25(海里),
∴DF=BD+BF=30+25=55(海里),
在Rt△DCF中,根据勾股定理,得
CD===70(海里),
∴70÷42=(小时).
答:救援船到达C点需要的最少时间是小时.
21.解:(1)由题意,CD=8×15=120(m),
在Rt△ACD中,tan∠ADC=,
∴AC=CD tan∠ADC=CD tan60°=120×=120(m),
答:无人机的高度AC是120米;
(2)过点B作BF⊥CD于点F,则四边形ABFC是矩形,
∴BF=AC=120,AB=CF,
在Rt△BEF中,tan∠BEF=,
∴EF==≈276.8(m),
∵CE=8×(15+50)=520(m),
∴AB=CF=CE﹣EF=520﹣276.8≈243(米),
答:隧道AB的长度约为243米.
一.选择题(共7小题,满分35分)
1.如图,要得到从点D观测点A的俯角,可以测量( )
A.∠DAB B.∠DCE C.∠DCA D.∠ADC
2.如图,小明在学校门口的点C处测得树的顶端A仰角为α,同时测得AC=15m,则树的高度AB为( )
A. B.15tanαm C. D.15sinαm
3.如图,一艘海轮位于灯塔P的南偏东37°方向,距离灯塔40海里的A处,它沿正北方向航行一段时间后,到达位于灯塔的正东方向上的B处,这时,B处与灯塔P的距离PB的长可以表示为( )
A.40海里 B.40sin37°海里
C.40cos37°海里 D.40tan37°海里
4.如图,某建筑物的顶部有一块标识牌CD,小明在斜坡上B处测得标识牌顶部C的仰角为45°,沿斜坡走下来在地面A处测得标识牌底部D的仰角为60°,已知斜坡AB的坡角为30°,AB=AE=10米.则标识牌CD的高度是( )米.
A.15﹣5 B.20﹣10 C.10﹣5 D.5﹣5
5.如图,在热气球C处测得地面A、B两点的俯角分别为30°、45°,热气球C的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是( )
A.200米 B.200米 C.220米 D.米
6.如图,王师傅在楼顶上A点处测得楼前一棵树CD的顶端C的俯角为60°,若水平距离BD=10m,楼高AB=24m,则树CD高约为( )
A.5m B.6m C.7m D.8m
7.某测量队在山脚A处测得山上树顶仰角为45°(如图),测量队在山坡上前进600米到D处,再测得树顶的仰角为60°,已知这段山坡的坡角为30°,如果树高为15米,则山高为( )(精确到1米,=1.732).
A.585米 B.1014米 C.805米 D.820米
二.填空题(共6小题,满分30分)
8.如图,一艘轮船位于灯塔P的南偏东60°方向,距离灯塔50海里的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东45°方向上的B处,此时B处与灯塔P的距离为 海里(结果保留根号).
9.如图,一艘轮船由西向东航行,在点B处测得小岛A位于它的东北方向,此时轮船与小岛A相距20nmile,继续航行至点D处,测得小岛A在它的北偏西60°方向,此时轮船与小岛的距离AD为 nmile(结果保留根号).
10.一艘轮船在小岛A的北偏东60°方向距小岛60海里的B处,沿正西方向航行3小时后到达小岛的北偏西45°的C处,则该船行驶的速度为 海里/小时.
11.如图,某海监船以30海里/小时的速度在某海域执行巡航任务,当海监船由西向东航行至A处时,测得岛屿P恰好在其正北方向,继续向东航行1小时到达B处,测得岛屿P在其北偏西30°方向,保持航向不变又航行2小时到达C处,此时海监船与岛屿P之间的距离(即PC的长)为 海里.
12.如图,在一次夏令营活动中,小明从营地A出发,沿北偏东53°方向走了400m到达B点,然后再沿北偏西37°方向走了300m到达目的地C.此时A,C两点之间的距离为 m.
13.小明想要测量水面人工岛上两棵小树CD的距离,如图,已知河岸MN∥CD,小明在河岸MN上点A处测量小树C位于北偏东60°方向,然后沿河岸走了20米,到达点B处,此时测得河对岸小树C位于北偏东30°方向,小树D位于东北方向,则两棵树CD的距离为 米.(结果保留根号)
三.解答题(共8小题,满分55分)
14.清代《修武县志》有胜果寺的记载,“康熙五十二年三月十七日,塔顶现青白二气如云,越二日乃止”,此文中的塔即为“胜果寺塔”.是修武作为“千年古县”的标志性古建筑,为了测量塔的高度,某校数学兴趣小组的两名同学采用了如下方式进行测量.如图,小明站在A处,眼睛E距离地面的高度为1.85m,测得塔顶C的仰角为45°,小红站在距离小明10m的D处,眼睛F距离地面的高度为1.5m,测得塔顶C的仰角为60°,已知A,D,塔底B在同一水平面上,由此即可求出塔高BC.你知道是怎么求的吗?请写出解题过程.(结果精确到1m.参考数据:=1.732)
15.如图,一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东39°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(结果精确到0.01小时,sin39°≈0.629,cos39°≈0.777,tan39°≈0.810)
16.如图,公园里有一棵大树(AB)与一棵小树(CD),受测量工具、地理环境及安全等因素影响不能直接测量它们的高度之差,小明与小丽手中有一副含30°角的直角三角尺和一根皮尺,小明首先在与树根B、D成一条直线的点E处用三角尺测得小树CD顶部C的仰角为30°,然后他向后移动调整,在M处用三角尺测得大树AB顶部A的仰角也是30°,点M仍然与B、D在一条直线上,然后他俩用皮尺测得BD=4.5米,EM=1.5米,求两棵树的高度之差.
17.如图,一楼房AB后有一假山,CD的坡度为i=1:2,山坡坡面上E点处有一休息亭,测得假山脚与楼房水平距离BC=20米,与亭子距离CE=6米,小丽从楼房房顶测得E的俯角为45°.
求:(1)点E到水平地面的距离;
(2)楼房AB的高.
18.今年是建党100周年,学校新装了国旗旗杆(如图所示),星期一该校全体学生在国旗前举行了升旗仪式.仪式结束后,站在国旗正前方的小明在A处测得国旗D处的仰角为45°,站在同一队列B处的小刚测得国旗C处的仰角为23°,已知小明目高AE=1.4米,距旗杆CG的距离为15.8米,小刚目高BF=1.8米,距小明24.2米,求国旗的宽度CD是多少米?(最后结果保留一位小数)
(参考数据:sin23°≈0.3907,cos23°≈0.9205,tan23°≈0.4245)
19.小张早起在一条东西走向的笔直马路上晨跑,他在A处时,D处学校和E处图书馆都在他的东北方向,当小张沿正东方向跑了600m到达B处时,E处图书馆在他的北偏东15°方向,然后他由B处继续向正东方向跑600m到达C处,此时D处学校在他的北偏西63.4°方向,求D处学校和E处图书馆之间的距离.(结果保留整数)
(参考数据:sin63.4°≈0.9,cos63.4°≈0.4,tan63.4°≈2.0,≈1.4,≈1.7,≈2.4)
20.如图,A,B是海面上位于东西方向的两个观测点,有一艘海轮在C点处遇险发出求救信号,此时测得C点位于观测点A的北偏东45°方向上,同时位于观测点B的北偏西60°方向上,且测得C点与观测点A的距离为25海里.
(1)求观测点B与C点之间的距离;
(2)有一艘救援船位于观测点B的正南方向且与观测点B相距30海里的D点处,在接到海轮的求救信号后立即前往营救,其航行速度为42海里/小时,求救援船到达C点需要的最少时间.
21.如图,某地政府为解决当地农户网络销售农特产品物流不畅问题,计划打通一条东西方向的隧道AB.无人机从点A的正上方点C,沿正东方向以8m/s的速度飞行15s到达点D,测得A的俯角为60°,然后以同样的速度沿正东方向又飞行50s到达点E,测得点B的俯角为37°.
(1)求无人机的高度AC(结果保留根号);
(2)求AB的长度(结果精确到1m).
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,≈1.73)
参考答案
一.选择题(共7小题,满分35分)
1.解:从点D观测点A的俯角即从点A观测点D的仰角,即∠DAB.
故选:A.
2.解:在Rt△ABC中,AC=15m,∠ACB=α,sinα=,
∴AB=AC sinα=15sinα(m),
故选:D.
3.解:∵一艘海轮位于灯塔P的南偏东37°方向,
∴∠BAP=37°,
∵AP=40海里,
∴BP=AP sin37°=40sin37°海里;
故选:B.
4.解:过点B作BM⊥EA的延长线于点M,过点B作BN⊥CE于点N,如图所示.
在Rt△ABM中,AB=10米,∠BAM=30°,
∴AM=AB cos∠BAM=5米,BM=AB sin∠BAM=5米.
在Rt△ADE中,AE=10米,∠DAE=60°,
∴DE=AE tan∠DAE=10米.
在Rt△BCN中,BN=AE+AM=(10+5)米,∠CBN=45°,
∴CN=BN tan∠CBN=(10+5)米,
∴CD=CN+EN﹣DE=10+5+5﹣10=(15﹣5)米.
故选:A.
5.解:∵在热气球C处测得地面B点的俯角为45°,
∴BD=CD=100米,
∵在热气球C处测得地面A点的俯角为30°,
∴AC=2×100=200米,
∴AD==100米,
∴AB=AD+BD=100+100=100(1+)米,
故选:D.
6.解:过C作CE⊥AB,交AB于点E,
在Rt△ACE中,∠EAC=30°,CE=10m,
∴AC=2CE=20m,AE==10m,
则CD=EB=AB﹣AE=24﹣10≈7m.
故选:C.
7.解:过点D作DF⊥AC于F.
在直角△ADF中,AF=AD cos30°=300米,DF=AD=300米.
设FC=x,则AC=300+x.
在直角△BDE中,BE=DE=x,则BC=300+x.
在直角△ACB中,∠BAC=45°.
∴这个三角形是等腰直角三角形.
∴AC=BC.
∴300+x=300+x.
解得:x=300.
∴BC=AC=300+300.
∴山高是300+300﹣15=285+300≈805米.
故选:C.
二.填空题(共6小题,满分30分)
8.解:过P作PC⊥AB于C,如图所示:
由题意得:∠APC=30°,∠BPC=45°,PA=50海里,
在Rt△APC中,cos∠APC=,
∴PC=PA cos∠APC=50×=25(海里),
在Rt△PCB中,cos∠BPC=,
∴PB===25(海里),
故答案为:25.
9.解:作AC⊥BD于点C,
由已知可得,∠BAC=45°,∠DAC=60°,AB=20nmile,
∵AC⊥BD,
∴∠ACB=∠ACD=90°,
∴AC=AB cos45°=20×=10(nmile),
∴AD===20(nmile),
故答案为:20.
10.解:如图所示:
设该船行驶的速度为x海里/时,
3小时后到达小岛的北偏西45°的C处,
由题意得:AB=60海里,BC=3x海里,
在直角三角形ABQ中,∠BAQ=60°,
∴∠B=90°﹣60°=30°,
∴AQ=AB=30,BQ=AQ=30,
在直角三角形AQC中,∠CAQ=45°,
∴CQ=AQ=30,
∴BC=30+30=3x,
解得:x=10+10(海里/时).
即该船行驶的速度为(10+10)海里/时;
故答案为:10+10.
11.解:在Rt△PAB中,∠APB=30°,
∴PB=2AB,
由题意得BC=2AB,
∴PB=BC,
∴∠C=∠CPB,
∵∠ABP=∠C+∠CPB=60°,
∴∠C=30°,
∴PC=2PA,
∵PA=AB tan60°,AB=30×1=30(海里),
∴PC=2×30×=60(海里),
故答案为:60.
12.解:如图,由题意得:AB=400m,BC=300m,∠CBD=37°,∠BAF=53°,AF∥DE,
∴∠ABE=∠BAF=53°,
∴∠ABC=180°﹣∠CBD﹣∠ABE=180°﹣37°﹣53°=90°,
∴AC===500(m),
即A,C两点之间的距离为500m,
故答案为:500.
13.解:如图所示,过点C作CE⊥MN于点E,过点D作DF⊥MN于点F,
设BE=a,
在Rt△BCE中,∵∠BCE=30°,
∴CE===a,
在Rt△ACE中,∵∠CAE=30°,AB=20,
∴由tan∠CAE=可得=,
解得a=10,
∴BE=10,DF=CE=10,
在Rt△BDF中,∵∠DBF=45°,
∴BF=DF=10,
∴CD=EF=BF﹣BE=10﹣10(米),
故答案为:(10﹣10).
三.解答题(共8小题,满分55分)
14.解:过E点作EG⊥BC于G,过F点作FH⊥BC于H,
设BC=xm,则CG=(x﹣1.85)m,CH=(x﹣1.5)m,
在Rt△CHF中,FH==,
Rt△CGE中,EG==(x﹣1.85)m,
∵EG﹣FH=10,
∴(x﹣1.85)﹣=10,
解得x≈26.
故塔高BC大约26m高.
15.解:如图,过点C作CD⊥AB交AB延长线于D.
在Rt△ACD中,∵∠ADC=90°,∠CAD=30°,AC=80海里,
∴CD=AC=40海里.
在Rt△CBD中,∵∠CDB=90°,∠BCD=39°,
∴BC==海里,
∴海警船到大事故船C处所需的时间大约为:÷40=≈1.29(小时).
答:海警船到大事故船C处所需的大约时间为1.29小时.
16.解:如图,延长NF交AB于点G,交CD于点H,
根据题意可知:
四边形BGHD,四边形DHFE,四边形FNME是矩形,
∴GH=BD=4.5米,HF=DE,FN=EM=1.5米,
在Rt△ANG中,∠AGN=90°,∠ANG=30°,
∴AG=GN tan∠ANG
=(GH+HF+FN) tan30°
=(4.5+HF+1.5)
=(6+HF)(米),
在Rt△CFH中,∠CHF=90°,∠CFH=30°,
∴CH=HF tan∠CFH
=HF tan30°
=HF,
∴AB﹣CD=(AG+BG)﹣(CH+DH)
=AG﹣CH
=(6+HF)﹣HF
=2 (米).
答:大树AB比小树CD高2米.
17.解:(1)如图,过点E作EF⊥BC的延长线于F,EH⊥AB于点H,
在Rt△CEF中,
∵CD的坡度为i=1:2,CE=6米,
∵i===tan∠ECF,
∴EF=6米,CF=12米,
∴BH=EF=6(米),
(2)∵HE=BF=BC+CF=20+12=32(米),
在Rt△AHE中,∠HAE=45°,
∴AH=HE=32(米),
∴AB=AH+HB=32+6=38(米).
答:楼房AB的高为38米.
18.解:作EM⊥CG于M,FN⊥CG于N,
由题意得GB=AG+AB=15.8+24.2=40(米),
则FN=GB=40米,
在Rt△EDM中,∠DEM=45°,
∴DM=EM=15.8米,
∵MG=AE=1.4米,
∴DG=DM+MG=15.8+1.4=17.2(米),
∵NG=FB=1.8米,
∴DN=17.2﹣1.8=15.4(米),
在Rt△CNF中,∠CFN=23°,
∵tan∠CFN=≈0.4245,
∴CN=0.4245×40≈17.0(米),
∴CD=CN﹣DN=17.0﹣15.4=1.6(米)
故国旗的宽度CD约为1.6米.
19.解:过D作DM⊥AC于M,
设MD=x,
在Rt△MAD中,∠MAD=45°,
∴△ADM是等腰直角三角形,
∴AM=MD=x,
∴AD=x,
在Rt△MCD中,∠MDC=63.4°,
∴MC≈2MD=2x,
∵AC=600+600=1200,
∴x+2x=1200,
解得:x=400,
∴MD=400m,
∴AD=MD=400,
过B作BN⊥AE于N,
∵∠EAB=45°,∠EBC=75°,
∴∠E=30°,
在Rt△ABN中,∠NAB=45°,AB=600,
∴BN=AN=AB=300,
∴DN=AD﹣AN=400﹣300=100,
在Rt△NBE中,∠E=30°,
∴NE=BN=×300=300,
∴DE=NE﹣DN=300﹣100≈580(m),
即D处学校和E处图书馆之间的距离约是580m.
20.解:(1)如图,过点C作CE⊥AB于点E,
根据题意可知:∠ACE=∠CAE=45°,AC=25海里,
∴AE=CE=25(海里),
∵∠CBE=30°,
∴BE=25(海里),
∴BC=2CE=50(海里).
答:观测点B与C点之间的距离为50海里;
(2)如图,作CF⊥DB于点F,
∵CF⊥DB,FB⊥EB,CE⊥AB,
∴四边形CEBF是矩形,
∴FB=CE=25(海里),CF=BE=25(海里),
∴DF=BD+BF=30+25=55(海里),
在Rt△DCF中,根据勾股定理,得
CD===70(海里),
∴70÷42=(小时).
答:救援船到达C点需要的最少时间是小时.
21.解:(1)由题意,CD=8×15=120(m),
在Rt△ACD中,tan∠ADC=,
∴AC=CD tan∠ADC=CD tan60°=120×=120(m),
答:无人机的高度AC是120米;
(2)过点B作BF⊥CD于点F,则四边形ABFC是矩形,
∴BF=AC=120,AB=CF,
在Rt△BEF中,tan∠BEF=,
∴EF==≈276.8(m),
∵CE=8×(15+50)=520(m),
∴AB=CF=CE﹣EF=520﹣276.8≈243(米),
答:隧道AB的长度约为243米.
