2021-2022学年京改版数学七年级上册3.4 点、线、面、体 课后培优卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年京改版数学七年级上册3.4 点、线、面、体 课后培优卷(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 271.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 11:54:11 | ||
图片预览


文档简介
3.4 点、 线、面、体
一、单选题
1.下列几何体中,面的个数最多的是( )
A. B. C. D.
2.下列立体图形的面都是平面的是( )
A.球 B.圆锥 C.圆柱 D.棱柱
3.如果一个n棱柱有18个顶点,那么底面边数n以及面数m分别为( )
A., B., C., D.,
4.一个棱柱有10个顶点,所有侧棱长的和是40cm,则每条侧棱长是( )
A.7cm B.8cm C.9cm D.10cm
5.生活中我们见到,时钟的秒针旋转形成一个圆面,可解释为( )
A.点动成线 B.线动成面 C.面动成体 D.以上答案都不对
6.如图是一个直六棱柱,它的棱共有多少条( ).
A.6 B.8 C.12 D.18
7.用一个平面去截下列选项中的几何体,截面不可能是圆的是( )
A. B.
C. D.
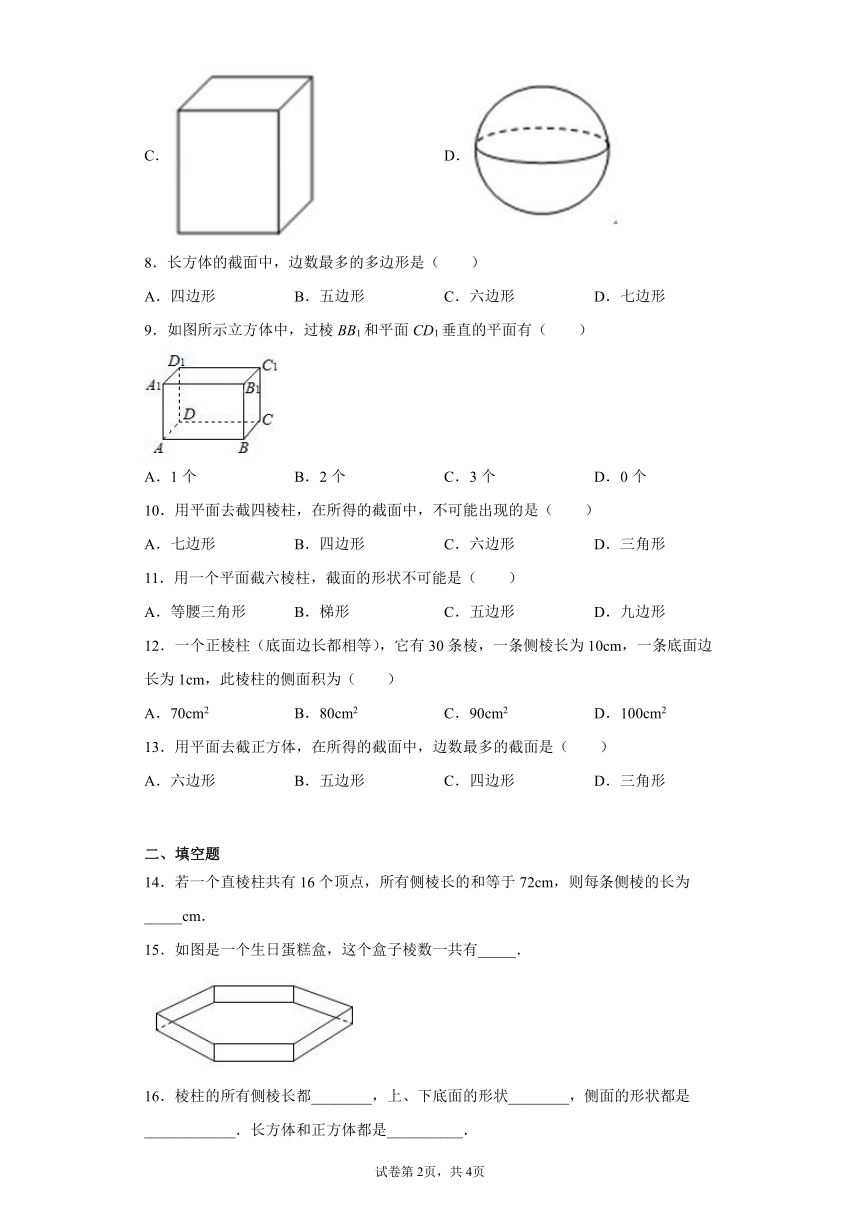
8.长方体的截面中,边数最多的多边形是( )
A.四边形 B.五边形 C.六边形 D.七边形
9.如图所示立方体中,过棱BB1和平面CD1垂直的平面有( )
A.1个 B.2个 C.3个 D.0个
10.用平面去截四棱柱,在所得的截面中,不可能出现的是( )
A.七边形 B.四边形 C.六边形 D.三角形
11.用一个平面截六棱柱,截面的形状不可能是( )
A.等腰三角形 B.梯形 C.五边形 D.九边形
12.一个正棱柱(底面边长都相等),它有30条棱,一条侧棱长为10cm,一条底面边长为1cm,此棱柱的侧面积为( )
A.70cm2 B.80cm2 C.90cm2 D.100cm2
13.用平面去截正方体,在所得的截面中,边数最多的截面是( )
A.六边形 B.五边形 C.四边形 D.三角形
二、填空题
14.若一个直棱柱共有16个顶点,所有侧棱长的和等于72cm,则每条侧棱的长为_____cm.
15.如图是一个生日蛋糕盒,这个盒子棱数一共有_____.
16.棱柱的所有侧棱长都________,上、下底面的形状________,侧面的形状都是____________.长方体和正方体都是__________.
17.用一个平面去截一个三棱锥,截面可能是_____形或_______形.
18.直棱柱的特征有:(1)两个底面_____________,(2)侧面都是____________;(3)侧棱__________底面,(4)两侧棱的关系是____________.
19.在一个棱柱中,一共有个面,则这个棱柱有________条棱.
三、解答题
20.如图,第一行的图形绕虚线旋转一周,能形成第二行的某个几何体,用线连起来.
21.如图所示的图形是一个棱柱,请问:
(1)这个棱柱由几个面组成?各面的交线有几条?
(2)这个棱柱的底面和侧面各是什么形状?
(3)该棱柱有几个顶点?
22.如图所示,在长方形ABCD中,BC=6cm,CD=8cm.现绕这个长方形的一边所在直线旋转一周得到一个几何体请解决以下问题:
(1)说出旋转得到的几何体的名称?
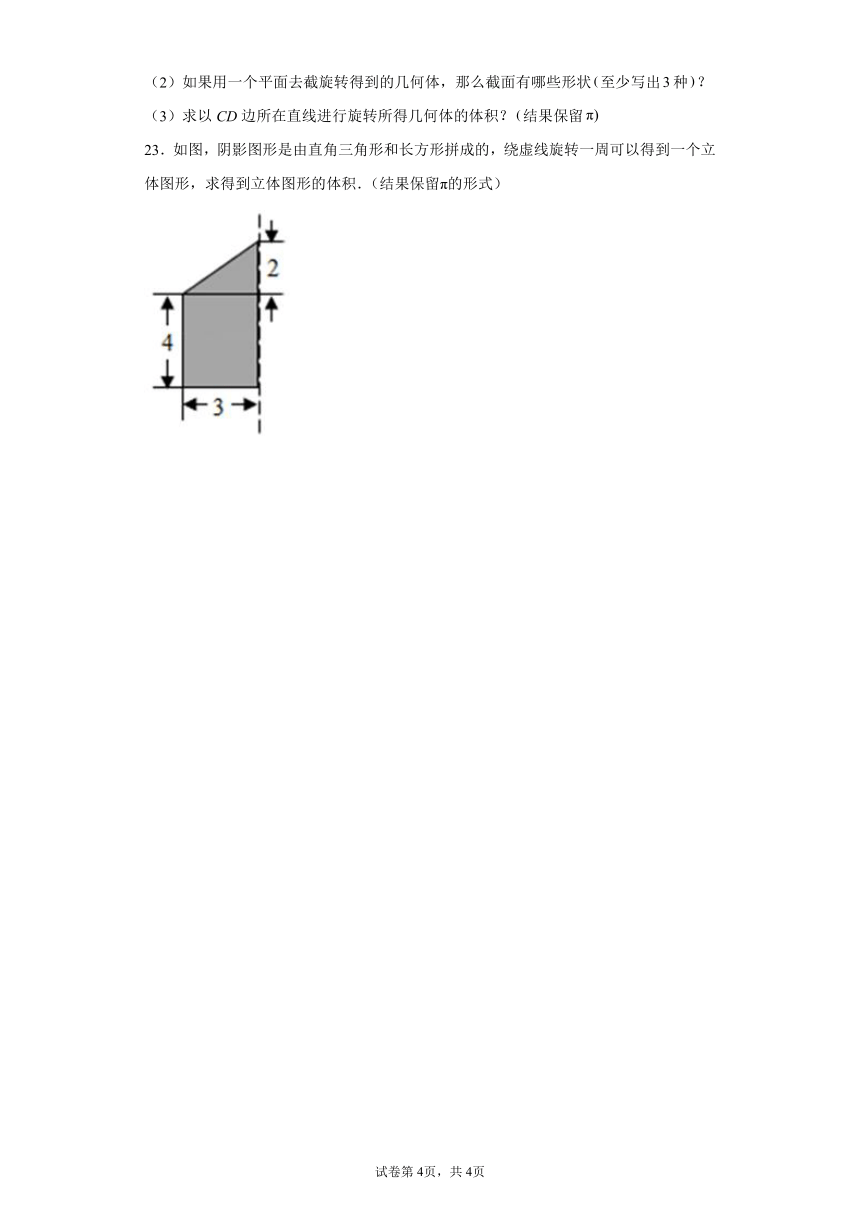
(2)如果用一个平面去截旋转得到的几何体,那么截面有哪些形状至少写出种?
(3)求以CD边所在直线进行旋转所得几何体的体积?结果保留
23.如图,阴影图形是由直角三角形和长方形拼成的,绕虚线旋转一周可以得到一个立体图形,求得到立体图形的体积.(结果保留π的形式)
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.C
解:A选项有一个底面一个侧面,共两个面;
B选项有两个底面三个侧面,共五个面;
C选项有两个底面四个侧面,共六个面;
D选项有两个底面一个侧面,共三个面;
故选:C.
2.D
解:球面是曲面,故A选项不符合题意;
圆锥的侧面是曲面,故B不符合题意;
圆锥的侧面是曲面,故C不符合题意;
棱柱的每一个面都是平面,故D符合题意;
故选D.
3.B
解:由题意得: ,
.
故选:B
4.B
解:∵棱柱有10个顶点,
∴棱柱为5棱柱,共有5条侧棱,
∵棱柱的侧棱长都相等,
∴每条侧棱长为40÷5=8.
故选B.
5.B
从运动的观点来看点动成线,线动成面,面动成体,可知生活中我们见到的时钟的秒针旋转形成一个圆面,可解释为:线动成面,
故选B
6.D
∵是直六棱柱,
∴共有18条棱;
故选D.
7.C
解:.圆柱体用平行于底面的截面去截,所得到的截面是圆形的,因此选项不符合题意;
.圆锥体用平行于底面的截面去截,所得到的截面是圆形的,因此选项不符合题意;
.由于四棱柱的六个面都是长方形的,用一个平面去截,得到的截面是多边形的,不可能出现圆形,因此选项符合题意;
.用一个平面沿着任意方向去截球体,所得到的截面都是圆形的,因此选项不符合题意;
故选:C.
8.C
解:长方体有六个面,截面与其六个面相交最多得六边形.
故选C.
9.A
解:过棱BB1和平面CD1垂直的平面有CBB1C1,所以只有1个.
故选:A.
10.A
解:四棱柱有六个面,用平面去截四棱柱时最多与六个面相交得六边形,最少与三个面相交得三角形.因此不可能是七边形.
故选:A.
11.D
解:用平面去截一个六棱柱,得的截面可能为三角形、四边形、五边形、六边形、七边形、八边形,不可能为九边形.
故选:D.
12.D
解:∵一个正棱柱(底面边长都相等),它有30条棱,
∴,
∴这个正棱柱是正十棱柱,
∴棱柱的侧面积;
故选D.
13.A
解:∵用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形,
∴边数最多的截面是六边形,
故选A.
14.9
解:直棱柱共有16个顶点,可知此棱柱为棱柱,有8个侧棱,且每个侧棱都相等
由此可知每条侧棱的长为
故答案为:9.
15.18
解:由题意得:这个盒子是六棱柱,
∴一共有18条棱,
故答案是:18.
16.相等 相同 平行四边形 四棱柱
解:棱柱的所有侧棱长都相等,上、下底面的形状相同,侧面的形状都是平行四边形.长方体和正方体都是四棱柱.
故答案为:相等;相同;平行四边形;四棱柱.
17.三角 四边
解:用平面去截一个三棱锥,截面可能为三角形或四边形.
故答案为:三角;四边.
18.相互平行且全等 矩形 垂直 相互平行且相等
直棱柱的两个底面相互平行且全等,侧面都是矩形,侧棱垂直底面,两个侧棱相互平行且相等;
故答案为:相互平行,矩形,垂直,相互平行且相等.
19.9
解:一个棱柱中,一共有5个面,则有2个底面,3个侧面,因此此立体图形是三棱柱,则这个棱柱棱的条数有9条.
故答案为:9.
20.答案见解析
连线如图:
21.(1)5,9;(2)棱柱的底面是三角形,侧面是平行四边形;(3)6
解:(1)这个棱柱有5个面组成,各面的交线有9条;
(2)棱柱的底面是三角形,侧面是平行四边形;
(3)该棱柱有6个顶点.
22.(1)圆柱;(2)长方形或圆形或梯形;(3)
解:(1)长方形绕一边旋转一周,得到圆柱;
(2)如果用一个平面去截这个圆柱,
则截面可能是:长方形或圆形或梯形;
(3)当以CD为边所在直线进行旋转,得到的是底面半径为6cm,高为8cm的圆柱,
则体积为:=.
23.
解:阴影图形旋转一周得到的立体图形是圆锥和圆柱.
圆锥的体积,
圆柱的体积,
故立体图形的体积是.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.下列几何体中,面的个数最多的是( )
A. B. C. D.
2.下列立体图形的面都是平面的是( )
A.球 B.圆锥 C.圆柱 D.棱柱
3.如果一个n棱柱有18个顶点,那么底面边数n以及面数m分别为( )
A., B., C., D.,
4.一个棱柱有10个顶点,所有侧棱长的和是40cm,则每条侧棱长是( )
A.7cm B.8cm C.9cm D.10cm
5.生活中我们见到,时钟的秒针旋转形成一个圆面,可解释为( )
A.点动成线 B.线动成面 C.面动成体 D.以上答案都不对
6.如图是一个直六棱柱,它的棱共有多少条( ).
A.6 B.8 C.12 D.18
7.用一个平面去截下列选项中的几何体,截面不可能是圆的是( )
A. B.
C. D.
8.长方体的截面中,边数最多的多边形是( )
A.四边形 B.五边形 C.六边形 D.七边形
9.如图所示立方体中,过棱BB1和平面CD1垂直的平面有( )
A.1个 B.2个 C.3个 D.0个
10.用平面去截四棱柱,在所得的截面中,不可能出现的是( )
A.七边形 B.四边形 C.六边形 D.三角形
11.用一个平面截六棱柱,截面的形状不可能是( )
A.等腰三角形 B.梯形 C.五边形 D.九边形
12.一个正棱柱(底面边长都相等),它有30条棱,一条侧棱长为10cm,一条底面边长为1cm,此棱柱的侧面积为( )
A.70cm2 B.80cm2 C.90cm2 D.100cm2
13.用平面去截正方体,在所得的截面中,边数最多的截面是( )
A.六边形 B.五边形 C.四边形 D.三角形
二、填空题
14.若一个直棱柱共有16个顶点,所有侧棱长的和等于72cm,则每条侧棱的长为_____cm.
15.如图是一个生日蛋糕盒,这个盒子棱数一共有_____.
16.棱柱的所有侧棱长都________,上、下底面的形状________,侧面的形状都是____________.长方体和正方体都是__________.
17.用一个平面去截一个三棱锥,截面可能是_____形或_______形.
18.直棱柱的特征有:(1)两个底面_____________,(2)侧面都是____________;(3)侧棱__________底面,(4)两侧棱的关系是____________.
19.在一个棱柱中,一共有个面,则这个棱柱有________条棱.
三、解答题
20.如图,第一行的图形绕虚线旋转一周,能形成第二行的某个几何体,用线连起来.
21.如图所示的图形是一个棱柱,请问:
(1)这个棱柱由几个面组成?各面的交线有几条?
(2)这个棱柱的底面和侧面各是什么形状?
(3)该棱柱有几个顶点?
22.如图所示,在长方形ABCD中,BC=6cm,CD=8cm.现绕这个长方形的一边所在直线旋转一周得到一个几何体请解决以下问题:
(1)说出旋转得到的几何体的名称?
(2)如果用一个平面去截旋转得到的几何体,那么截面有哪些形状至少写出种?
(3)求以CD边所在直线进行旋转所得几何体的体积?结果保留
23.如图,阴影图形是由直角三角形和长方形拼成的,绕虚线旋转一周可以得到一个立体图形,求得到立体图形的体积.(结果保留π的形式)
试卷第1页,共3页
试卷第1页,共3页
参考答案
1.C
解:A选项有一个底面一个侧面,共两个面;
B选项有两个底面三个侧面,共五个面;
C选项有两个底面四个侧面,共六个面;
D选项有两个底面一个侧面,共三个面;
故选:C.
2.D
解:球面是曲面,故A选项不符合题意;
圆锥的侧面是曲面,故B不符合题意;
圆锥的侧面是曲面,故C不符合题意;
棱柱的每一个面都是平面,故D符合题意;
故选D.
3.B
解:由题意得: ,
.
故选:B
4.B
解:∵棱柱有10个顶点,
∴棱柱为5棱柱,共有5条侧棱,
∵棱柱的侧棱长都相等,
∴每条侧棱长为40÷5=8.
故选B.
5.B
从运动的观点来看点动成线,线动成面,面动成体,可知生活中我们见到的时钟的秒针旋转形成一个圆面,可解释为:线动成面,
故选B
6.D
∵是直六棱柱,
∴共有18条棱;
故选D.
7.C
解:.圆柱体用平行于底面的截面去截,所得到的截面是圆形的,因此选项不符合题意;
.圆锥体用平行于底面的截面去截,所得到的截面是圆形的,因此选项不符合题意;
.由于四棱柱的六个面都是长方形的,用一个平面去截,得到的截面是多边形的,不可能出现圆形,因此选项符合题意;
.用一个平面沿着任意方向去截球体,所得到的截面都是圆形的,因此选项不符合题意;
故选:C.
8.C
解:长方体有六个面,截面与其六个面相交最多得六边形.
故选C.
9.A
解:过棱BB1和平面CD1垂直的平面有CBB1C1,所以只有1个.
故选:A.
10.A
解:四棱柱有六个面,用平面去截四棱柱时最多与六个面相交得六边形,最少与三个面相交得三角形.因此不可能是七边形.
故选:A.
11.D
解:用平面去截一个六棱柱,得的截面可能为三角形、四边形、五边形、六边形、七边形、八边形,不可能为九边形.
故选:D.
12.D
解:∵一个正棱柱(底面边长都相等),它有30条棱,
∴,
∴这个正棱柱是正十棱柱,
∴棱柱的侧面积;
故选D.
13.A
解:∵用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形,
∴边数最多的截面是六边形,
故选A.
14.9
解:直棱柱共有16个顶点,可知此棱柱为棱柱,有8个侧棱,且每个侧棱都相等
由此可知每条侧棱的长为
故答案为:9.
15.18
解:由题意得:这个盒子是六棱柱,
∴一共有18条棱,
故答案是:18.
16.相等 相同 平行四边形 四棱柱
解:棱柱的所有侧棱长都相等,上、下底面的形状相同,侧面的形状都是平行四边形.长方体和正方体都是四棱柱.
故答案为:相等;相同;平行四边形;四棱柱.
17.三角 四边
解:用平面去截一个三棱锥,截面可能为三角形或四边形.
故答案为:三角;四边.
18.相互平行且全等 矩形 垂直 相互平行且相等
直棱柱的两个底面相互平行且全等,侧面都是矩形,侧棱垂直底面,两个侧棱相互平行且相等;
故答案为:相互平行,矩形,垂直,相互平行且相等.
19.9
解:一个棱柱中,一共有5个面,则有2个底面,3个侧面,因此此立体图形是三棱柱,则这个棱柱棱的条数有9条.
故答案为:9.
20.答案见解析
连线如图:
21.(1)5,9;(2)棱柱的底面是三角形,侧面是平行四边形;(3)6
解:(1)这个棱柱有5个面组成,各面的交线有9条;
(2)棱柱的底面是三角形,侧面是平行四边形;
(3)该棱柱有6个顶点.
22.(1)圆柱;(2)长方形或圆形或梯形;(3)
解:(1)长方形绕一边旋转一周,得到圆柱;
(2)如果用一个平面去截这个圆柱,
则截面可能是:长方形或圆形或梯形;
(3)当以CD为边所在直线进行旋转,得到的是底面半径为6cm,高为8cm的圆柱,
则体积为:=.
23.
解:阴影图形旋转一周得到的立体图形是圆锥和圆柱.
圆锥的体积,
圆柱的体积,
故立体图形的体积是.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 有理数
- 1.1 负数的引入
- 1.2 用数轴上的点表示有理数
- 1.3 相反数和绝对值
- 1.4 有理数的加法
- 1.5 有理数的减法
- 1.6 有理数加减法的混合运算
- 1.7 有理数的乘法
- 1.8 有理数的除法
- 1.9 有理数的乘方
- 1.10 有理数的混合运算
- 1.11 数的近似和科学记数法
- 1.12 用计算器做有理数的混合运算
- 第二章 一元一次方程
- 2.1 字母表示数
- 2.2 同类项与合并同类项
- 2.3 等式与方程
- 2.4 等式的基本性质
- 2.5 一元一次方程
- 2.6 列方程解应用问题
- 第三章 简单的几何图形
- 3.1 平面图形与立体图形
- 3.2 某些立体图形的展开图
- 3.3 从不同方向观察立体图形
- 3.4 点、线、面、体
- 3.5 直线、射线、线段
- 3.6 角及其分类
- 3.7 角的度量与角的换算
- 3.8 角平分线
- 3.9 两条直线的位置关系
- 3.10 相交线与平行线
- 3.11 用计算机绘图
