2021-2022学年京改版数学八年级上册12.5 全等三角形的判定 同步训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年京改版数学八年级上册12.5 全等三角形的判定 同步训练(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 376.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 11:59:35 | ||
图片预览

文档简介
12.5 全等三角形的判定
一、单选题
1.下列命题不正确的是( )
A.成轴对称的两个三角形一定是全等三角形
B.周长相等的两个三角形一定是全等三角形
C.边长相等的两个等边三角形一定是全等三角形
D.面积相等的两个等边三角形一定是全等三角形
2.如图,OA=OB,点C、D分别在OA、OB上,AD、BC相交于点E,且∠A=∠B.有下列3个结论:①,②,③点E在∠O的平分线上.其中,正确的结论是( )
A.只有① B.只有② C.只有①② D.①②③
3.下列条件中,能判断两个三角形全等的是( )
A.两边和它们的夹角分别相等 B.两边及其中一边所对的角分别相等
C.三个角分别相等 D.两个三角形面积相等
4.如图下列各组条件中,可以判定△ABC≌△DEF的条件是( )
A.∠A=∠D、∠B=∠E、∠C=∠F B.AB=DE、AC=DF、BC=EF
C.AB=DE、AC=DF、∠C=∠F D.BC=EF、∠A=∠D、∠B=∠F
5.如图,在中,过点A作的平分线的垂线交内部于点P,交边于点D,连结,若,的面积分别为4、2,则的面积是( )
A.24 B.12 C.8 D.6
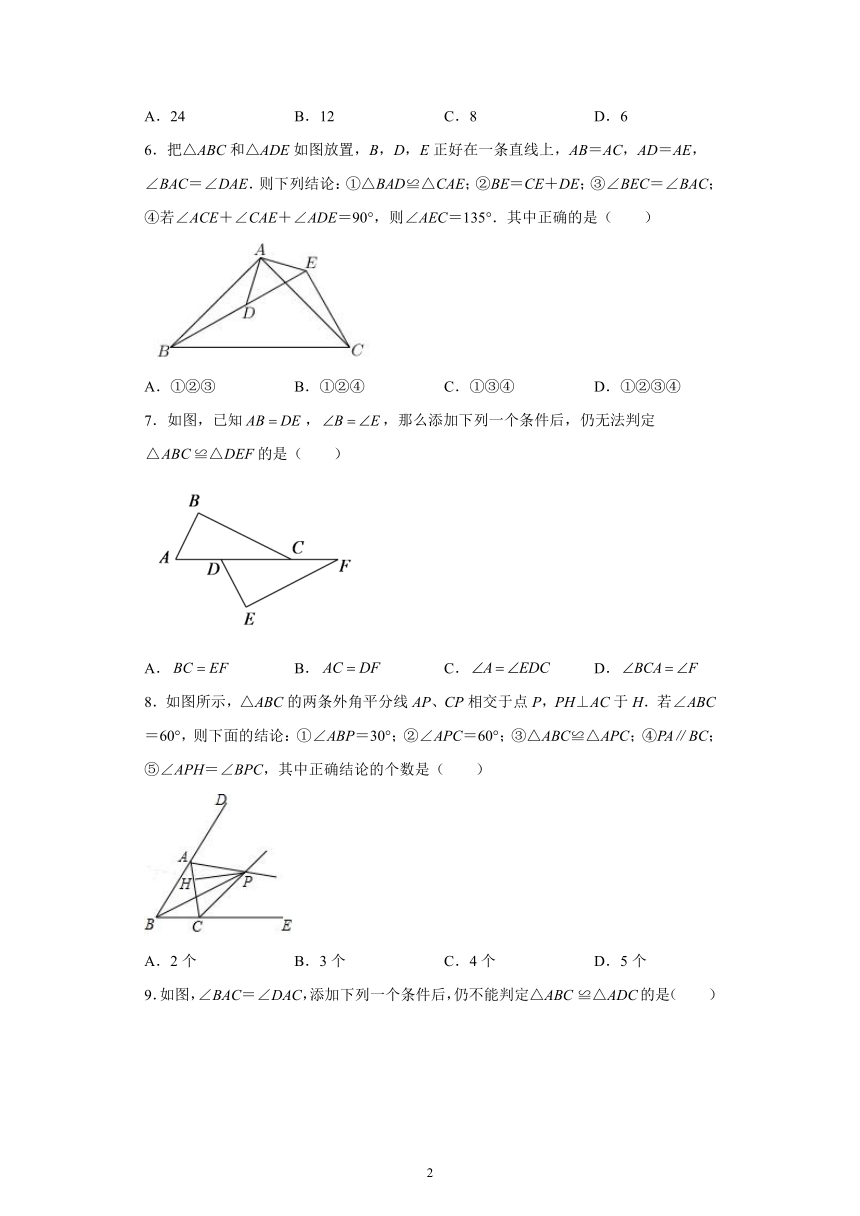
6.把△ABC和△ADE如图放置,B,D,E正好在一条直线上,AB=AC,AD=AE,∠BAC=∠DAE.则下列结论:①△BAD≌△CAE;②BE=CE+DE;③∠BEC=∠BAC;④若∠ACE+∠CAE+∠ADE=90°,则∠AEC=135°.其中正确的是( )
A.①②③ B.①②④ C.①③④ D.①②③④
7.如图,已知,,那么添加下列一个条件后,仍无法判定的是( )
A. B. C. D.
8.如图所示,△ABC的两条外角平分线AP、CP相交于点P,PH⊥AC于H.若∠ABC=60°,则下面的结论:①∠ABP=30°;②∠APC=60°;③△ABC≌△APC;④PA∥BC;⑤∠APH=∠BPC,其中正确结论的个数是( )
A.2个 B.3个 C.4个 D.5个
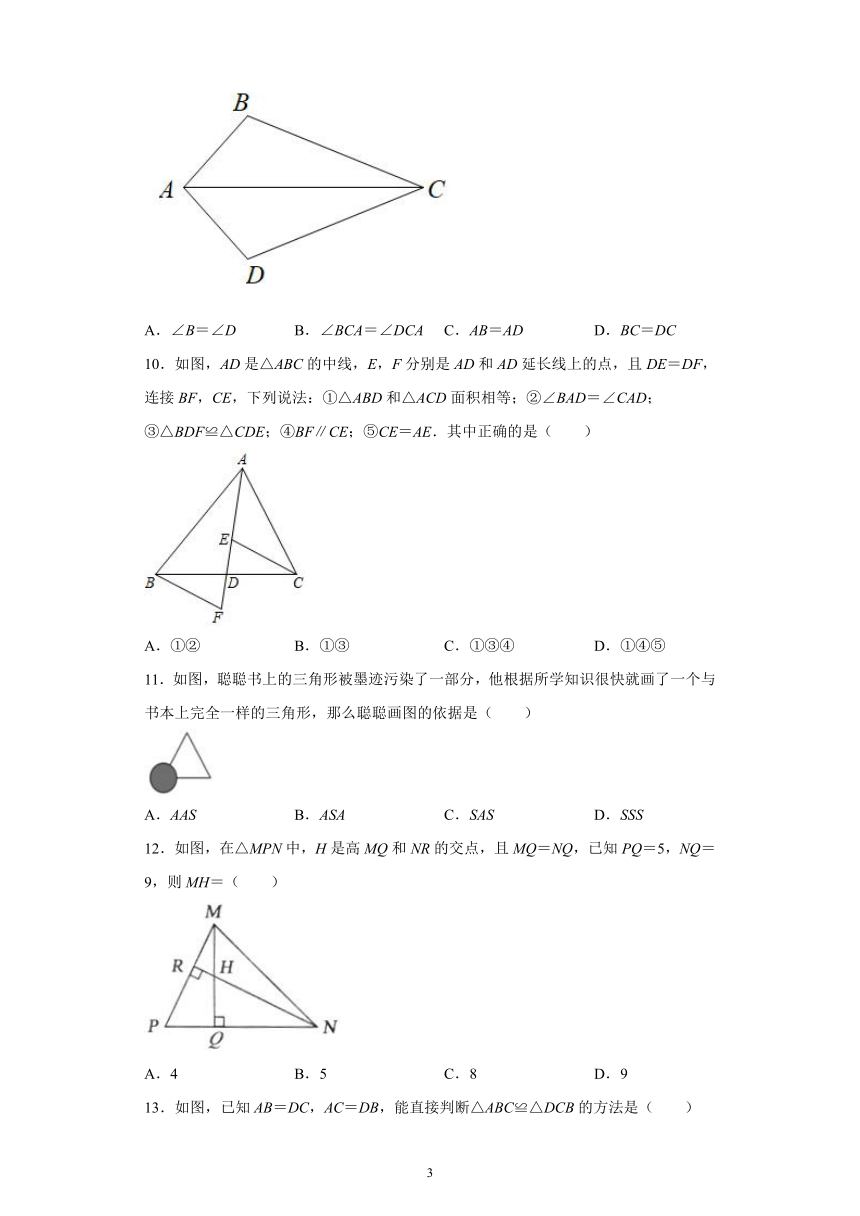
9.如图,∠BAC=∠DAC,添加下列一个条件后,仍不能判定△ABC ≌△ADC的是( )
A.∠B=∠D B.∠BCA=∠DCA C.AB=AD D.BC=DC
10.如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE,下列说法:①△ABD和△ACD面积相等;②∠BAD=∠CAD;③△BDF≌△CDE;④BF∥CE;⑤CE=AE.其中正确的是( )
A.①② B.①③ C.①③④ D.①④⑤
11.如图,聪聪书上的三角形被墨迹污染了一部分,他根据所学知识很快就画了一个与书本上完全一样的三角形,那么聪聪画图的依据是( )
A.AAS B.ASA C.SAS D.SSS
12.如图,在△MPN中,H是高MQ和NR的交点,且MQ=NQ,已知PQ=5,NQ=9,则MH=( )
A.4 B.5 C.8 D.9
13.如图,已知AB=DC,AC=DB,能直接判断△ABC≌△DCB的方法是( )
A.SAS B.AAS C.SSS D.ASA
二、填空题
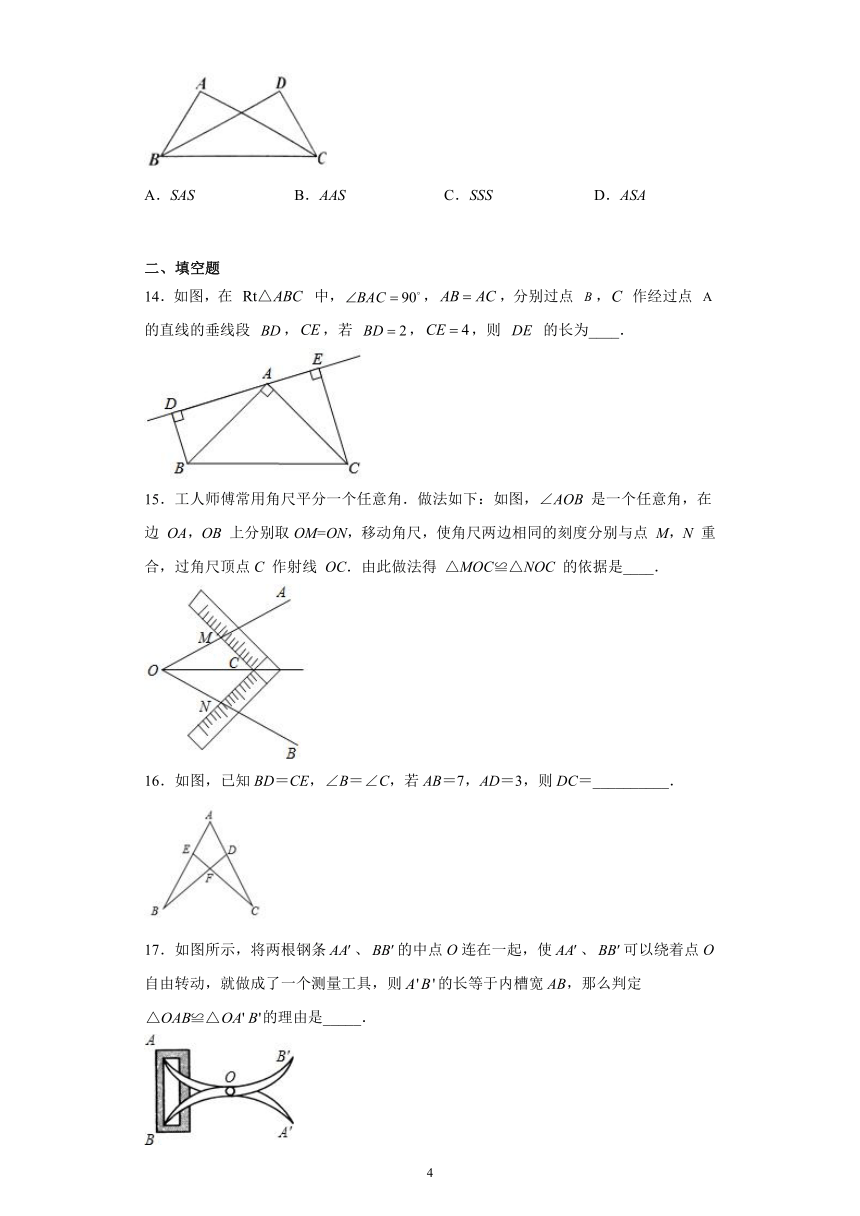
14.如图,在 中,,,分别过点 , 作经过点 的直线的垂线段 ,,若 ,,则 的长为____.
15.工人师傅常用角尺平分一个任意角.做法如下:如图,∠AOB 是一个任意角,在边 OA,OB 上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点 M,N 重合,过角尺顶点C 作射线 OC.由此做法得 △MOC≌△NOC 的依据是____.
16.如图,已知BD=CE,∠B=∠C,若AB=7,AD=3,则DC=__________.
17.如图所示,将两根钢条、的中点O连在一起,使、可以绕着点O自由转动,就做成了一个测量工具,则的长等于内槽宽AB,那么判定的理由是_____.
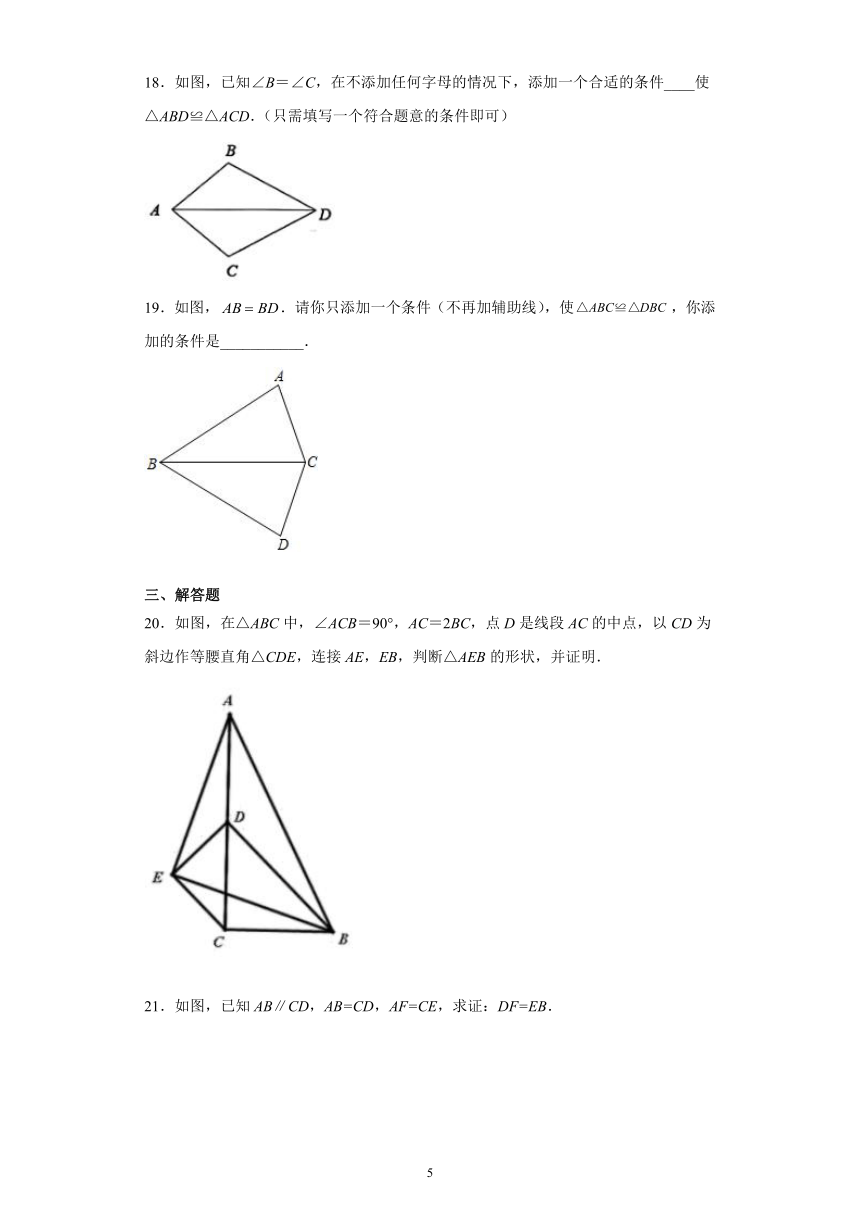
18.如图,已知∠B=∠C,在不添加任何字母的情况下,添加一个合适的条件____使△ABD≌△ACD.(只需填写一个符合题意的条件即可)
19.如图,.请你只添加一个条件(不再加辅助线),使,你添加的条件是___________.
三、解答题
20.如图,在△ABC中,∠ACB=90°,AC=2BC,点D是线段AC的中点,以CD为斜边作等腰直角△CDE,连接AE,EB,判断△AEB的形状,并证明.
21.如图,已知AB∥CD,AB=CD,AF=CE,求证:DF=EB.
22.如图,△ABC中,∠ACB=90°,点D,E分别在边BC,AC上,DE=DB,∠DEC=∠B.
求证:AD平分∠BAC.
23.如图,AB=CD,∠B=∠C,点F、E在BC上,BF=CE.求证:AE=DF.
参考答案
1.B
解:A、根据轴对称的性质可得,两个三角形的边长对应相等,所以两个三角全等,说法正确,不符合题意;
B、周长相等的两个三角形,不一定相等,说法错误,符合题意;
C、边长相等的两个等边三角形,对应边相等,两个三角形全等,说法正确,不符合题意;
D、面积相等的两个等边三角形,对应边相等,两个三角形全等,说法正确,不符合题意;
故选B
2.D
解:∵在与中,
,
,故①正确;
,
,
,
∵在与中,
,
,故②正确;
,
连接,
∵在与中,
,
,
,
点在的平分线上,故③正确,
∴正确的结论有①②③,
故选:D.
3.A
解:A、根据SAS定理可判定两个三角形全等,故此选项正确;
B、SSA不能证明两个三角形全等,故此选项错误;
C、AAA不能证明两个三角形全等,故此选项错误;
D、不能证明两个三角形全等,故此选项错误;
故选:A.
4.B
解:A、没有边的条件,不符合全等三角形的判定定理,即不能推出△ABC≌△DEF,故本选项不合题意;
B、符合全等三角形的判定定理SSS,即能推出△ABC≌△DEF,故本选项符合题意;
C、只满足SSA,不符合全等三角形的判定定理,即不能推出△ABC≌△DEF,故本选项不合题意;
D、只能判定△ABC≌△DFE,故本选项不合题意;
故选B.
5.B
由题可得:,,
,
在与中,
,
,
,
,,
.
故选:B.
6.D
解:∵,
∴,即.
又∵AB=AC,AD=AE,
∴,故①正确.
∴BD=CE.
∵BE=BD+DE,
∴BE=CE+DE,故②正确.
∵,
∴.
又∵,,
∴,故③正确.
∵,
∴,.
∵,
∴.
∴.
∴.
∵AD=AE,
∴.
∴.
又∵,,
∴.
∴,故④正确.
故选:D.
7.B
解:A、添加可以利用进行判定,此选项不符合题意;
B、添加无法利用进行判定,此选项符合题意;
C、添加可以利用进行判定,此选项不符合题意;
D、添加可以利用进行判定,此选项不符合题意;
故选:B.
8.B
如图,作PM⊥BC于M,PN⊥BA于N.
∵∠PAH=∠PAN,PN⊥AD,PH⊥AC,
∴PN=PH,同理PM=PH,
∴PN=PM,
∴PB平分∠ABC,
∴∠ABP=∠ABC=30°,故①正确,
∵在Rt△PAH和Rt△PAN中,
,
∴△PAN≌△PAH,同理可证,△PCM≌△PCH,
∴∠APN=∠APH,∠CPM=∠CPH,
∵∠MPN=180°-∠ABC=120°,
∴∠APC=∠MPN=60°,故②正确,
在△ABC和△APC中,仅可得到,不能得到△ABC≌△APC;故③不正确,
的角度未知,不能得到PA∥BC;故④不正确
∵∠BPN=∠CPA=60°,
∴∠CPB=∠APN=∠APH,故⑤正确.
综上,正确的结论为①②⑤.
故选B.
9.D
解:根据题意可知∠BAC=∠DAC,,
当∠B=∠D时,可由“角角边”证明 △ABC ≌△ADC,
故A选项能判定△ABC ≌△ADC,不符合题意;
当∠BCA=∠DCA,时可由“角边角”证明 △ABC ≌△ADC,
故B选项能判定△ABC ≌△ADC,不符合题意;
当AB=AD时,可由“边角边”证明 △ABC ≌△ADC,
故C选项能判定△ABC ≌△ADC,不符合题意;
当BC=DC时,则“边边角”不能证明 △ABC ≌△ADC,
故D选项不能判定△ABC ≌△ADC,符合题意;
故选:D.
10.C
解:∵AD是△ABC的中线,
∴BD=CD,
∴△ABD和△ACD面积相等,故①正确;
∵AD为△ABC的中线,
∴BD=CD,∠BAD和∠CAD不一定相等,故②错误;
在△BDF和△CDE中,
,
∴△BDF≌△CDE(SAS),故③正确;
∴∠F=∠DEC,
∴BF∥CE,故④正确;
∵△BDF≌△CDE,
∴CE=BF,故⑤错误,
正确的结论为:①③④,
故选:C.
11.B
根据题意,三角形的两角和它们的夹边是完整的,所以可以利用“角边角”定理作出完全一样的三角形.
故选B.
12.A
解:∵MQ⊥PN,NR⊥PM,
∴∠NQH=∠NRP=∠HRM=90°,
∵∠RHM=∠QHN,
∴∠PMH=∠HNQ,
在△MQP和△NQH中,
,
∴△MQP≌△NQH(ASA),
∴PQ=QH=5,
∵NQ=MQ=9,
∴MH=MQ HQ=9 5=4,
故选:A.
13.C
解:∵AB=DC,AC=DB,BC=CB,
∴△ABC≌△DCB(SSS),
故选:C.
14.
解:∵BD⊥DE,CE⊥DE,BA⊥AC,
∴∠BDA=∠BAC=∠AEC=90°,
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠ABD=∠CAE,
在△ABD和△CAE中,
,
∴△ABD≌△CAE(AAS),
∴DB=AE=2,CE=AD=4,
则DE=AD+AE=4+2=6.
故答案为:6.
15.SSS边边边
解:∵在△ONC和△OMC中,
∴△MOC≌△NOC(SSS),
∴∠BOC=∠AOC,
故答案为:SSS.
16.4
在△ABD和△ACE中,,
∴△ABD≌△ACE,
∴AC=AB,
∵AB=7,AD=3,
∴CD=AC-AD=AB-AD=7-3=4.
故答案为:4
17.SAS
解:∵OA=OA′,OB=OB′,∠AOB=∠A′OB′,
∴△OAB≌△OA′B′(SAS)
所以理由是SAS.
故答案为:SAS.
18.∠CAD=∠BAD(或∠CDA=∠BDA)
解:需添加的一个条件是:∠CAD=∠BAD,
理由:∵在△ABD和△ACD中,
,
∴△ABD≌△ACD(AAS).
故答案为:∠CAD=∠BAD(或∠CDA=∠BDA).
19.
解:添加条件为,使,
证明如下:
在中,
,
.
20.△AEB是等腰直角三角形,理由见解析.
解:△AEB是等腰直角三角形,理由如下:
∵△CDE是等腰直角三角形,
∴ED=EC,∠EDC=∠ECD=45°,
∵∠ACB=90°,
∴∠EDA+∠EDC=180°,
∴∠ECB=∠ECD+∠ACB=45°+90°=135°,
∠EDA=180°-45°=135°,
∴∠ECB=∠EDA,
∵点D是线段AC的中点,
∴AC=2AD,
∵AC=2BC,
∴AD=BC,
在△ADE和△BCE中,
,
∴△ADE≌△BCE(SAS),
∴EA=EB,∠AED=∠BEC,
∵∠DEC=∠DEB+∠BEC=90°,
∴∠AED+∠DEB=90°,
即∠AEB=90°,
又EA=EB,
∴△AEB是等腰直角三角形.
21.见解析
证明:∵ABCD,
∴∠A=∠C,
又∵AF=CE,
∴AF+EF=CE+EF,
即AE=CF,
在△ABE和△CDF中,,
∴△ABE≌△CDF(SAS),
∴DF=EB.
22.证明见解析
证明:过点D作,
∴,
∵∠ACB=90°,
∴,,
在和中,
,
∴,
∴,
∴点D在的平分线上,
∴AD平分;
23.见解析
证明:∵BF=CE,
∴BF+FE=CE+FE,
∴BE=CF,
在△ABE与△DCF中,
∵AB=DC,∠B=∠C,BE=CF,
∴△ABE≌△DCF(SAS).
∴AE=DF.
一、单选题
1.下列命题不正确的是( )
A.成轴对称的两个三角形一定是全等三角形
B.周长相等的两个三角形一定是全等三角形
C.边长相等的两个等边三角形一定是全等三角形
D.面积相等的两个等边三角形一定是全等三角形
2.如图,OA=OB,点C、D分别在OA、OB上,AD、BC相交于点E,且∠A=∠B.有下列3个结论:①,②,③点E在∠O的平分线上.其中,正确的结论是( )
A.只有① B.只有② C.只有①② D.①②③
3.下列条件中,能判断两个三角形全等的是( )
A.两边和它们的夹角分别相等 B.两边及其中一边所对的角分别相等
C.三个角分别相等 D.两个三角形面积相等
4.如图下列各组条件中,可以判定△ABC≌△DEF的条件是( )
A.∠A=∠D、∠B=∠E、∠C=∠F B.AB=DE、AC=DF、BC=EF
C.AB=DE、AC=DF、∠C=∠F D.BC=EF、∠A=∠D、∠B=∠F
5.如图,在中,过点A作的平分线的垂线交内部于点P,交边于点D,连结,若,的面积分别为4、2,则的面积是( )
A.24 B.12 C.8 D.6
6.把△ABC和△ADE如图放置,B,D,E正好在一条直线上,AB=AC,AD=AE,∠BAC=∠DAE.则下列结论:①△BAD≌△CAE;②BE=CE+DE;③∠BEC=∠BAC;④若∠ACE+∠CAE+∠ADE=90°,则∠AEC=135°.其中正确的是( )
A.①②③ B.①②④ C.①③④ D.①②③④
7.如图,已知,,那么添加下列一个条件后,仍无法判定的是( )
A. B. C. D.
8.如图所示,△ABC的两条外角平分线AP、CP相交于点P,PH⊥AC于H.若∠ABC=60°,则下面的结论:①∠ABP=30°;②∠APC=60°;③△ABC≌△APC;④PA∥BC;⑤∠APH=∠BPC,其中正确结论的个数是( )
A.2个 B.3个 C.4个 D.5个
9.如图,∠BAC=∠DAC,添加下列一个条件后,仍不能判定△ABC ≌△ADC的是( )
A.∠B=∠D B.∠BCA=∠DCA C.AB=AD D.BC=DC
10.如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE,下列说法:①△ABD和△ACD面积相等;②∠BAD=∠CAD;③△BDF≌△CDE;④BF∥CE;⑤CE=AE.其中正确的是( )
A.①② B.①③ C.①③④ D.①④⑤
11.如图,聪聪书上的三角形被墨迹污染了一部分,他根据所学知识很快就画了一个与书本上完全一样的三角形,那么聪聪画图的依据是( )
A.AAS B.ASA C.SAS D.SSS
12.如图,在△MPN中,H是高MQ和NR的交点,且MQ=NQ,已知PQ=5,NQ=9,则MH=( )
A.4 B.5 C.8 D.9
13.如图,已知AB=DC,AC=DB,能直接判断△ABC≌△DCB的方法是( )
A.SAS B.AAS C.SSS D.ASA
二、填空题
14.如图,在 中,,,分别过点 , 作经过点 的直线的垂线段 ,,若 ,,则 的长为____.
15.工人师傅常用角尺平分一个任意角.做法如下:如图,∠AOB 是一个任意角,在边 OA,OB 上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点 M,N 重合,过角尺顶点C 作射线 OC.由此做法得 △MOC≌△NOC 的依据是____.
16.如图,已知BD=CE,∠B=∠C,若AB=7,AD=3,则DC=__________.
17.如图所示,将两根钢条、的中点O连在一起,使、可以绕着点O自由转动,就做成了一个测量工具,则的长等于内槽宽AB,那么判定的理由是_____.
18.如图,已知∠B=∠C,在不添加任何字母的情况下,添加一个合适的条件____使△ABD≌△ACD.(只需填写一个符合题意的条件即可)
19.如图,.请你只添加一个条件(不再加辅助线),使,你添加的条件是___________.
三、解答题
20.如图,在△ABC中,∠ACB=90°,AC=2BC,点D是线段AC的中点,以CD为斜边作等腰直角△CDE,连接AE,EB,判断△AEB的形状,并证明.
21.如图,已知AB∥CD,AB=CD,AF=CE,求证:DF=EB.
22.如图,△ABC中,∠ACB=90°,点D,E分别在边BC,AC上,DE=DB,∠DEC=∠B.
求证:AD平分∠BAC.
23.如图,AB=CD,∠B=∠C,点F、E在BC上,BF=CE.求证:AE=DF.
参考答案
1.B
解:A、根据轴对称的性质可得,两个三角形的边长对应相等,所以两个三角全等,说法正确,不符合题意;
B、周长相等的两个三角形,不一定相等,说法错误,符合题意;
C、边长相等的两个等边三角形,对应边相等,两个三角形全等,说法正确,不符合题意;
D、面积相等的两个等边三角形,对应边相等,两个三角形全等,说法正确,不符合题意;
故选B
2.D
解:∵在与中,
,
,故①正确;
,
,
,
∵在与中,
,
,故②正确;
,
连接,
∵在与中,
,
,
,
点在的平分线上,故③正确,
∴正确的结论有①②③,
故选:D.
3.A
解:A、根据SAS定理可判定两个三角形全等,故此选项正确;
B、SSA不能证明两个三角形全等,故此选项错误;
C、AAA不能证明两个三角形全等,故此选项错误;
D、不能证明两个三角形全等,故此选项错误;
故选:A.
4.B
解:A、没有边的条件,不符合全等三角形的判定定理,即不能推出△ABC≌△DEF,故本选项不合题意;
B、符合全等三角形的判定定理SSS,即能推出△ABC≌△DEF,故本选项符合题意;
C、只满足SSA,不符合全等三角形的判定定理,即不能推出△ABC≌△DEF,故本选项不合题意;
D、只能判定△ABC≌△DFE,故本选项不合题意;
故选B.
5.B
由题可得:,,
,
在与中,
,
,
,
,,
.
故选:B.
6.D
解:∵,
∴,即.
又∵AB=AC,AD=AE,
∴,故①正确.
∴BD=CE.
∵BE=BD+DE,
∴BE=CE+DE,故②正确.
∵,
∴.
又∵,,
∴,故③正确.
∵,
∴,.
∵,
∴.
∴.
∴.
∵AD=AE,
∴.
∴.
又∵,,
∴.
∴,故④正确.
故选:D.
7.B
解:A、添加可以利用进行判定,此选项不符合题意;
B、添加无法利用进行判定,此选项符合题意;
C、添加可以利用进行判定,此选项不符合题意;
D、添加可以利用进行判定,此选项不符合题意;
故选:B.
8.B
如图,作PM⊥BC于M,PN⊥BA于N.
∵∠PAH=∠PAN,PN⊥AD,PH⊥AC,
∴PN=PH,同理PM=PH,
∴PN=PM,
∴PB平分∠ABC,
∴∠ABP=∠ABC=30°,故①正确,
∵在Rt△PAH和Rt△PAN中,
,
∴△PAN≌△PAH,同理可证,△PCM≌△PCH,
∴∠APN=∠APH,∠CPM=∠CPH,
∵∠MPN=180°-∠ABC=120°,
∴∠APC=∠MPN=60°,故②正确,
在△ABC和△APC中,仅可得到,不能得到△ABC≌△APC;故③不正确,
的角度未知,不能得到PA∥BC;故④不正确
∵∠BPN=∠CPA=60°,
∴∠CPB=∠APN=∠APH,故⑤正确.
综上,正确的结论为①②⑤.
故选B.
9.D
解:根据题意可知∠BAC=∠DAC,,
当∠B=∠D时,可由“角角边”证明 △ABC ≌△ADC,
故A选项能判定△ABC ≌△ADC,不符合题意;
当∠BCA=∠DCA,时可由“角边角”证明 △ABC ≌△ADC,
故B选项能判定△ABC ≌△ADC,不符合题意;
当AB=AD时,可由“边角边”证明 △ABC ≌△ADC,
故C选项能判定△ABC ≌△ADC,不符合题意;
当BC=DC时,则“边边角”不能证明 △ABC ≌△ADC,
故D选项不能判定△ABC ≌△ADC,符合题意;
故选:D.
10.C
解:∵AD是△ABC的中线,
∴BD=CD,
∴△ABD和△ACD面积相等,故①正确;
∵AD为△ABC的中线,
∴BD=CD,∠BAD和∠CAD不一定相等,故②错误;
在△BDF和△CDE中,
,
∴△BDF≌△CDE(SAS),故③正确;
∴∠F=∠DEC,
∴BF∥CE,故④正确;
∵△BDF≌△CDE,
∴CE=BF,故⑤错误,
正确的结论为:①③④,
故选:C.
11.B
根据题意,三角形的两角和它们的夹边是完整的,所以可以利用“角边角”定理作出完全一样的三角形.
故选B.
12.A
解:∵MQ⊥PN,NR⊥PM,
∴∠NQH=∠NRP=∠HRM=90°,
∵∠RHM=∠QHN,
∴∠PMH=∠HNQ,
在△MQP和△NQH中,
,
∴△MQP≌△NQH(ASA),
∴PQ=QH=5,
∵NQ=MQ=9,
∴MH=MQ HQ=9 5=4,
故选:A.
13.C
解:∵AB=DC,AC=DB,BC=CB,
∴△ABC≌△DCB(SSS),
故选:C.
14.
解:∵BD⊥DE,CE⊥DE,BA⊥AC,
∴∠BDA=∠BAC=∠AEC=90°,
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠ABD=∠CAE,
在△ABD和△CAE中,
,
∴△ABD≌△CAE(AAS),
∴DB=AE=2,CE=AD=4,
则DE=AD+AE=4+2=6.
故答案为:6.
15.SSS边边边
解:∵在△ONC和△OMC中,
∴△MOC≌△NOC(SSS),
∴∠BOC=∠AOC,
故答案为:SSS.
16.4
在△ABD和△ACE中,,
∴△ABD≌△ACE,
∴AC=AB,
∵AB=7,AD=3,
∴CD=AC-AD=AB-AD=7-3=4.
故答案为:4
17.SAS
解:∵OA=OA′,OB=OB′,∠AOB=∠A′OB′,
∴△OAB≌△OA′B′(SAS)
所以理由是SAS.
故答案为:SAS.
18.∠CAD=∠BAD(或∠CDA=∠BDA)
解:需添加的一个条件是:∠CAD=∠BAD,
理由:∵在△ABD和△ACD中,
,
∴△ABD≌△ACD(AAS).
故答案为:∠CAD=∠BAD(或∠CDA=∠BDA).
19.
解:添加条件为,使,
证明如下:
在中,
,
.
20.△AEB是等腰直角三角形,理由见解析.
解:△AEB是等腰直角三角形,理由如下:
∵△CDE是等腰直角三角形,
∴ED=EC,∠EDC=∠ECD=45°,
∵∠ACB=90°,
∴∠EDA+∠EDC=180°,
∴∠ECB=∠ECD+∠ACB=45°+90°=135°,
∠EDA=180°-45°=135°,
∴∠ECB=∠EDA,
∵点D是线段AC的中点,
∴AC=2AD,
∵AC=2BC,
∴AD=BC,
在△ADE和△BCE中,
,
∴△ADE≌△BCE(SAS),
∴EA=EB,∠AED=∠BEC,
∵∠DEC=∠DEB+∠BEC=90°,
∴∠AED+∠DEB=90°,
即∠AEB=90°,
又EA=EB,
∴△AEB是等腰直角三角形.
21.见解析
证明:∵ABCD,
∴∠A=∠C,
又∵AF=CE,
∴AF+EF=CE+EF,
即AE=CF,
在△ABE和△CDF中,,
∴△ABE≌△CDF(SAS),
∴DF=EB.
22.证明见解析
证明:过点D作,
∴,
∵∠ACB=90°,
∴,,
在和中,
,
∴,
∴,
∴点D在的平分线上,
∴AD平分;
23.见解析
证明:∵BF=CE,
∴BF+FE=CE+FE,
∴BE=CF,
在△ABE与△DCF中,
∵AB=DC,∠B=∠C,BE=CF,
∴△ABE≌△DCF(SAS).
∴AE=DF.
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
