2021-2022学年人教版九年级数学上册23.2.1 中心对称同步练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学上册23.2.1 中心对称同步练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 338.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 12:05:30 | ||
图片预览

文档简介
23.2.1 中心对称同步练习 2021-2022学年人教版九年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共6小题,共30分)
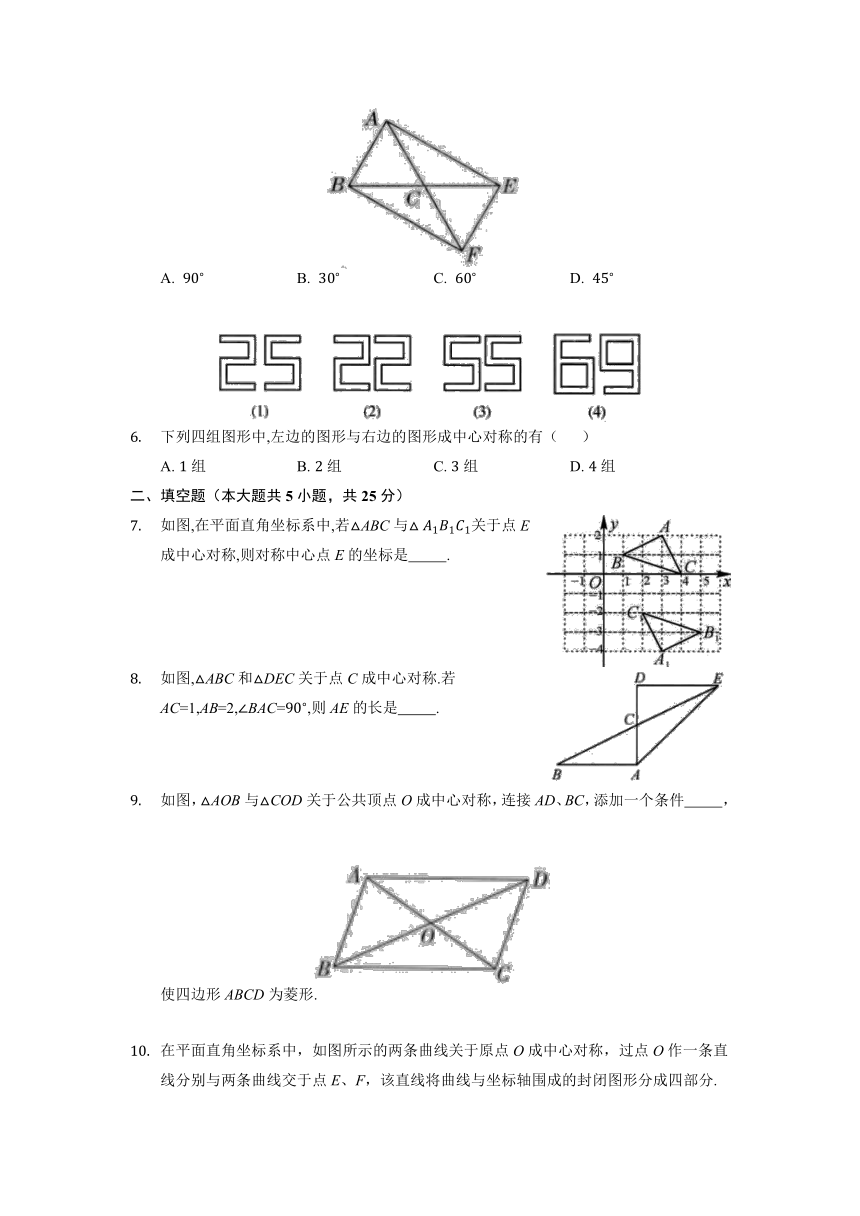
下列各组图形中,A'B'C'与ABC成中心对称的是( )
A. B.
C. D.
如图,ABC与A'B'C'关于点O成中心对称,则下列结论不成立的是( )
A.
B.
C.
D. 点在的延长线上
下列两个电子数字成中心对称的是( )
A. B. C. D.
如图,边长为2的正方形ABCD的对角线交于点O,过点O的直线分别交边AD,BC于E,F两点,则阴影部分的面积是( )
A. B.
C. D.
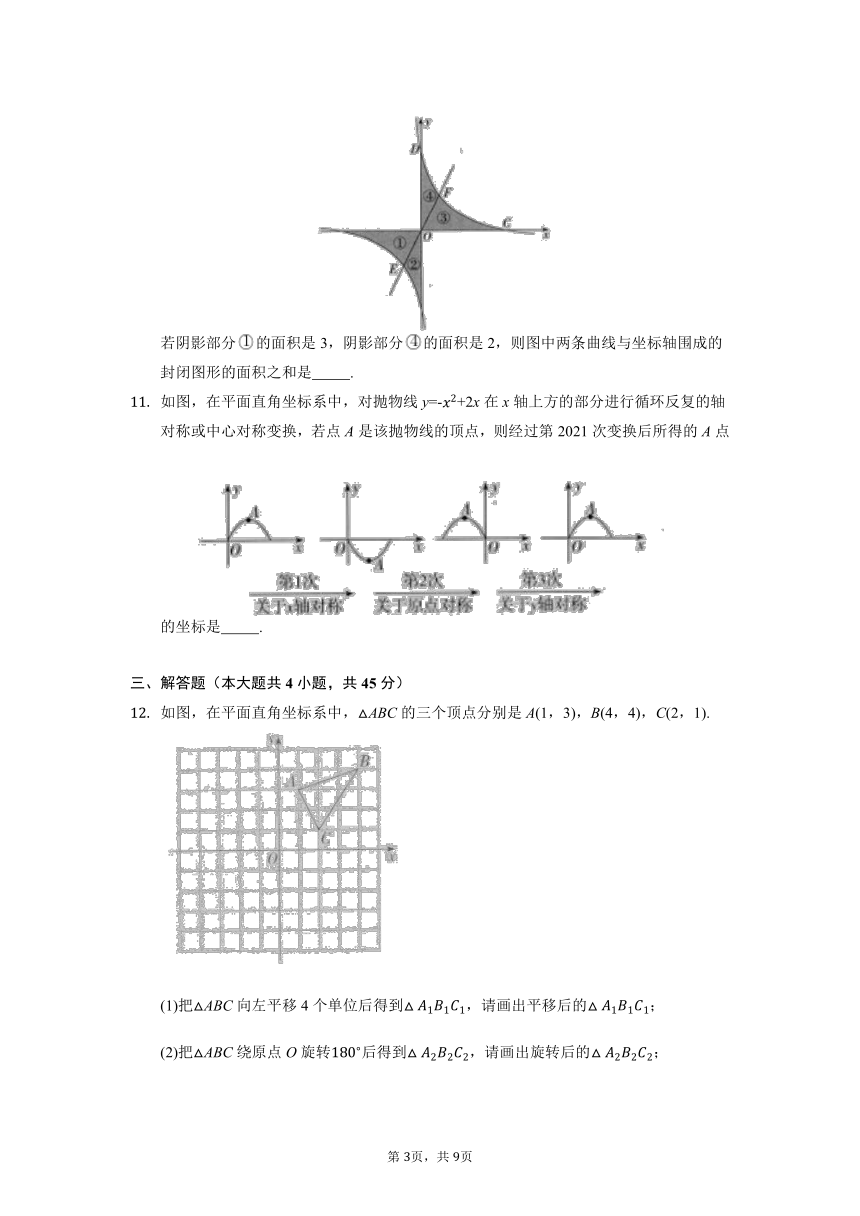
如图,在ABC中,AB=AC,ABC与FEC关于点C成中心对称,连接AE,BF,当BAE=时,ACB的度数为( )
A. B. C. D.
下列四组图形中,左边的图形与右边的图形成中心对称的有( )
A. 组 B. 组 C. 组 D. 组
二、填空题(本大题共5小题,共25分)
如图,在平面直角坐标系中,若ABC与关于点E成中心对称,则对称中心点E的坐标是 .
如图,ABC和DEC关于点C成中心对称.若AC=1,AB=2,BAC=,则AE的长是 .
如图,AOB与COD关于公共顶点O成中心对称,连接AD、BC,添加一个条件 ,使四边形ABCD为菱形.
在平面直角坐标系中,如图所示的两条曲线关于原点O成中心对称,过点O作一条直线分别与两条曲线交于点E、F,该直线将曲线与坐标轴围成的封闭图形分成四部分.若阴影部分的面积是3,阴影部分的面积是2,则图中两条曲线与坐标轴围成的封闭图形的面积之和是 .
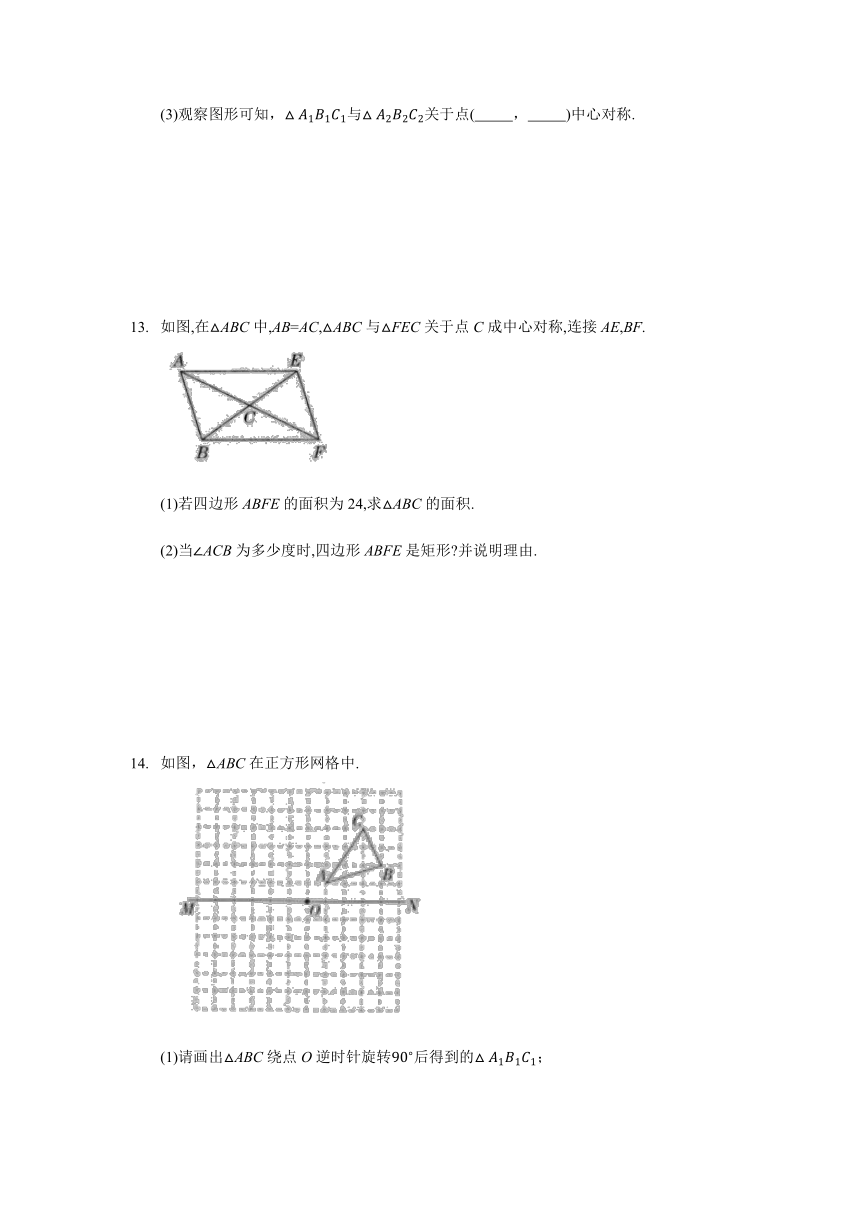
如图,在平面直角坐标系中,对抛物线y=-+2x在x轴上方的部分进行循环反复的轴对称或中心对称变换,若点A是该抛物线的顶点,则经过第2021次变换后所得的A点的坐标是 .
三、解答题(本大题共4小题,共45分)
如图,在平面直角坐标系中,ABC的三个顶点分别是A(1,3),B(4,4),C(2,1).
(1)把ABC向左平移4个单位后得到,请画出平移后的;
(2)把ABC绕原点O旋转后得到,请画出旋转后的;
(3)观察图形可知,与关于点( , )中心对称.
如图,在ABC中,AB=AC,ABC与FEC关于点C成中心对称,连接AE,BF.
(1)若四边形ABFE的面积为24,求ABC的面积.
(2)当ACB为多少度时,四边形ABFE是矩形 并说明理由.
如图,ABC在正方形网格中.
(1)请画出ABC绕点O逆时针旋转后得到的;
(2)请画出ABC关于点O成中心对称的;
(3)在直线MN上求作一点P,使PAB的周长最小,请画出PAB.
如图,在ABC中,A=,点D为BC的中点,DE DF,DE交AB于点E,DF交AC于点F,试探究线段BE,EF,FC之间的数量关系.
1.【答案】D
2.【答案】B
3.【答案】A
4.【答案】A
5.【答案】C
6.【答案】C
7.【答案】(3,-1)
8.【答案】2
9.【答案】AOB=(答案不唯一)
10.【答案】10
11.【答案】(-1,1)
12.【答案】解:(1)如图所示,即为所求.
(2)如图所示,即为所求.
(3)连接,线段的中点(-2,0)就是对称中心.
13.【答案】解:(1)ABC与FEC关于点C成中心对称,
点A,C,F共线,点B,C,E共线,AC=FC,BC=EC.
四边形ABFE是平行四边形.
==6.
(2)当ACB=时,四边形ABFE是矩形.理由如下:
AC=AB,ACB=,
ABC是等边三角形.
AC=BC.
又AC=CF=AF,BC=EC=BE,
AF=BE.
又四边形ABFE是平行四边形,
四边形ABFE是矩形.
14.【答案】(1)如图,即为所作.
(2)如图,即为所作.
(3)如图,点P及PAB即为所作.
15.【答案】解:点D为BC的中点,
BD=CD.
作BDE关于点D成中心对称的CDM,如图所示.
由中心对称的性质可得CM=BE,MD=ED,DCM=B,点M,D,E在一条直线上.
又B+ACB=,
DCM+ACB=,
即FCM=.连接FM.
在FME中,MD=ED,FDME,
FM=FE.
又在RtFCM中,
+=,
+=.
第1页,共1页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共6小题,共30分)
下列各组图形中,A'B'C'与ABC成中心对称的是( )
A. B.
C. D.
如图,ABC与A'B'C'关于点O成中心对称,则下列结论不成立的是( )
A.
B.
C.
D. 点在的延长线上
下列两个电子数字成中心对称的是( )
A. B. C. D.
如图,边长为2的正方形ABCD的对角线交于点O,过点O的直线分别交边AD,BC于E,F两点,则阴影部分的面积是( )
A. B.
C. D.
如图,在ABC中,AB=AC,ABC与FEC关于点C成中心对称,连接AE,BF,当BAE=时,ACB的度数为( )
A. B. C. D.
下列四组图形中,左边的图形与右边的图形成中心对称的有( )
A. 组 B. 组 C. 组 D. 组
二、填空题(本大题共5小题,共25分)
如图,在平面直角坐标系中,若ABC与关于点E成中心对称,则对称中心点E的坐标是 .
如图,ABC和DEC关于点C成中心对称.若AC=1,AB=2,BAC=,则AE的长是 .
如图,AOB与COD关于公共顶点O成中心对称,连接AD、BC,添加一个条件 ,使四边形ABCD为菱形.
在平面直角坐标系中,如图所示的两条曲线关于原点O成中心对称,过点O作一条直线分别与两条曲线交于点E、F,该直线将曲线与坐标轴围成的封闭图形分成四部分.若阴影部分的面积是3,阴影部分的面积是2,则图中两条曲线与坐标轴围成的封闭图形的面积之和是 .
如图,在平面直角坐标系中,对抛物线y=-+2x在x轴上方的部分进行循环反复的轴对称或中心对称变换,若点A是该抛物线的顶点,则经过第2021次变换后所得的A点的坐标是 .
三、解答题(本大题共4小题,共45分)
如图,在平面直角坐标系中,ABC的三个顶点分别是A(1,3),B(4,4),C(2,1).
(1)把ABC向左平移4个单位后得到,请画出平移后的;
(2)把ABC绕原点O旋转后得到,请画出旋转后的;
(3)观察图形可知,与关于点( , )中心对称.
如图,在ABC中,AB=AC,ABC与FEC关于点C成中心对称,连接AE,BF.
(1)若四边形ABFE的面积为24,求ABC的面积.
(2)当ACB为多少度时,四边形ABFE是矩形 并说明理由.
如图,ABC在正方形网格中.
(1)请画出ABC绕点O逆时针旋转后得到的;
(2)请画出ABC关于点O成中心对称的;
(3)在直线MN上求作一点P,使PAB的周长最小,请画出PAB.
如图,在ABC中,A=,点D为BC的中点,DE DF,DE交AB于点E,DF交AC于点F,试探究线段BE,EF,FC之间的数量关系.
1.【答案】D
2.【答案】B
3.【答案】A
4.【答案】A
5.【答案】C
6.【答案】C
7.【答案】(3,-1)
8.【答案】2
9.【答案】AOB=(答案不唯一)
10.【答案】10
11.【答案】(-1,1)
12.【答案】解:(1)如图所示,即为所求.
(2)如图所示,即为所求.
(3)连接,线段的中点(-2,0)就是对称中心.
13.【答案】解:(1)ABC与FEC关于点C成中心对称,
点A,C,F共线,点B,C,E共线,AC=FC,BC=EC.
四边形ABFE是平行四边形.
==6.
(2)当ACB=时,四边形ABFE是矩形.理由如下:
AC=AB,ACB=,
ABC是等边三角形.
AC=BC.
又AC=CF=AF,BC=EC=BE,
AF=BE.
又四边形ABFE是平行四边形,
四边形ABFE是矩形.
14.【答案】(1)如图,即为所作.
(2)如图,即为所作.
(3)如图,点P及PAB即为所作.
15.【答案】解:点D为BC的中点,
BD=CD.
作BDE关于点D成中心对称的CDM,如图所示.
由中心对称的性质可得CM=BE,MD=ED,DCM=B,点M,D,E在一条直线上.
又B+ACB=,
DCM+ACB=,
即FCM=.连接FM.
在FME中,MD=ED,FDME,
FM=FE.
又在RtFCM中,
+=,
+=.
第1页,共1页
同课章节目录
