2021-2022学年人教版九年级数学上册24.1.3 弧、弦、圆心角 同步测试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学上册24.1.3 弧、弦、圆心角 同步测试卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 144.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 12:05:36 | ||
图片预览


文档简介
24.1.3 弧、弦、圆心角同步测试卷 2021-2022学年人教版九年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共6小题,共30分)
下图中ACB是圆心角的是( )
A. B. C. D.
下列说法正确的是( )
A. 相等的圆心角所对的弧相等
B. 在同圆中,等弧所对的圆心角相等
C. 在同圆中,相等的弦所对的弧相等
D. 相等的弦所对的弧相等
如图,已知A,B,C,D是圆上的点,=,AC,BD交于点E,则下列结论正确的是( )
A. B.
C. D.
如图,已知A,B,C,D四点都在O上,OBAC,BC=CD,下列四个说法:=2;AC=2CD;OCBD;AOD=3BOC,其中正确的有( )
A. 个 B. 个
C. 个 D. 个
如图,MN是O的直径,点A是半圆上一个三等分点,点B是的中点,点B'是点B关于MN的对称点,O的半径为1,则AB'的长等于( )
A. B.
C. D.
如图,O的半径为1,动点P从点A处出发,沿圆周以每秒圆心角的速度逆时针匀速运动,即第1秒点P位于如图所示位置,第2秒点P位于点C的位置,,则第2019秒点P所在位置的坐标为( )
A. B.
C. D.
二、填空题(本大题共5小题,共25分)
如图,已知AB为O的直径,点D为半圆周上的一点,且所对圆心角的度数是所对圆心角度数的2倍,则圆心角BOD= .
如图,A,B,C,D是⊙O上的四个点,AD∥BC.那么与的数量关系是 .
如图,在O中,弦AB和弦CD所对圆心角的度数分别为和,则弦AB和弦CD长度的比= .
如图,A、B、C、D在O上,AB=BC=DA,AD、BC的延长线交于点P,且P=,则所对的圆心角的度数为 .
如图,已知点C,D是半圆上的三等分点,连接AC,BC,CD,OD,BC和OD相交于点E.则下列结论:CBA=;ODBC;OE=AC;四边形AODC是菱形.正确的有 .(填序号)
三、解答题(本大题共4小题,共45分)
如图,AB为O的直径,C,D是O上的两点,且BDOC.求证:=.
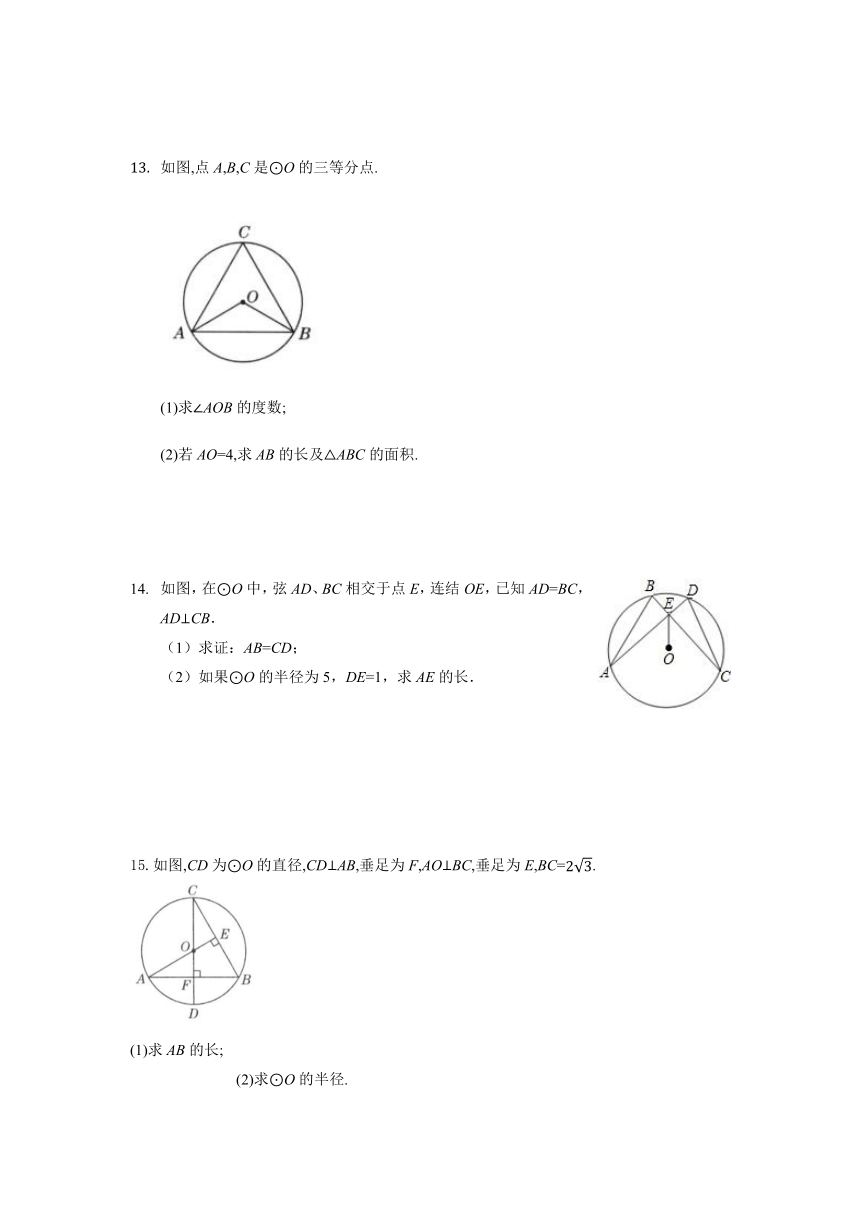
如图,点A,B,C是O的三等分点.
(1)求AOB的度数;
(2)若AO=4,求AB的长及ABC的面积.
如图,在⊙O中,弦AD、BC相交于点E,连结OE,已知AD=BC,AD⊥CB.
(1)求证:AB=CD;
(2)如果⊙O的半径为5,DE=1,求AE的长.
15.如图,CD为O的直径,CDAB,垂足为F,AOBC,垂足为E,BC=.
(1)求AB的长;
(2)求O的半径.
1.【答案】B
2.【答案】B
3.【答案】C
4.【答案】C
5.【答案】B
6.【答案】B
7.【答案】
8.【答案】=
9.【答案】
10.【答案】
11.【答案】
12.【答案】证明:OB=OD,
D=B.
BDOC,
D=COD,AOC=B.
AOC=COD.
=.
13.【答案】解:(1)如图,连接OC.
点A,B,C是O的三等分点,
==.
AOB=BOC=AOC==.
(2)如图,过点O作ODAB于点D,
则ODB=,BD=AB.
OA=OB,
OAB=OBA=(-AOB)=.
在RtBOD中,OBA=,
OD=OB=2.
BD===2.
AB=2BD=4.
OA=OB=OC,AOB=BOC=AOC,
AOBBOCAOC.
==.
==3ABOD=42=12.
14.【答案】(1)证明:如图,∵AD=BC,
∴=,
∴-=-,即=
∴AB=CD;
(2)解:如图,过O作OF⊥AD于点F,作OG⊥BC于点G,连接OA、OC.
则AF=FD,BG=CG.
∵AD=BC,
∴AF=CG.
在Rt△AOF与Rt△COG中,
,
∴Rt△AOF≌Rt△COG(HL),
∴OF=OG,
∴四边形OFEG是正方形,
∴OF=EF.
设OF=EF=x,则AF=FD=x+1,
在直角△OAF中.由勾股定理得到:x2+(x+1)2=52,
解得 x=3.
则AF=3+1=4,即AE=AF+3=7.
15.【答案】解:(1)连接AC,
CD为O的直径,CDAB,
=.
AC=BC.
又AOBC,
=.
AC=AB.AB=BC=2.
(2)由(1)知AB=BC=AC,
ABC为等边三角形.
B=.
OAF=.
CDAB,
AF=BF=,OF=AO.
在RtOAF中,=+,即=+,
OA=2,即O的半径为2.
第2页,共3页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共6小题,共30分)
下图中ACB是圆心角的是( )
A. B. C. D.
下列说法正确的是( )
A. 相等的圆心角所对的弧相等
B. 在同圆中,等弧所对的圆心角相等
C. 在同圆中,相等的弦所对的弧相等
D. 相等的弦所对的弧相等
如图,已知A,B,C,D是圆上的点,=,AC,BD交于点E,则下列结论正确的是( )
A. B.
C. D.
如图,已知A,B,C,D四点都在O上,OBAC,BC=CD,下列四个说法:=2;AC=2CD;OCBD;AOD=3BOC,其中正确的有( )
A. 个 B. 个
C. 个 D. 个
如图,MN是O的直径,点A是半圆上一个三等分点,点B是的中点,点B'是点B关于MN的对称点,O的半径为1,则AB'的长等于( )
A. B.
C. D.
如图,O的半径为1,动点P从点A处出发,沿圆周以每秒圆心角的速度逆时针匀速运动,即第1秒点P位于如图所示位置,第2秒点P位于点C的位置,,则第2019秒点P所在位置的坐标为( )
A. B.
C. D.
二、填空题(本大题共5小题,共25分)
如图,已知AB为O的直径,点D为半圆周上的一点,且所对圆心角的度数是所对圆心角度数的2倍,则圆心角BOD= .
如图,A,B,C,D是⊙O上的四个点,AD∥BC.那么与的数量关系是 .
如图,在O中,弦AB和弦CD所对圆心角的度数分别为和,则弦AB和弦CD长度的比= .
如图,A、B、C、D在O上,AB=BC=DA,AD、BC的延长线交于点P,且P=,则所对的圆心角的度数为 .
如图,已知点C,D是半圆上的三等分点,连接AC,BC,CD,OD,BC和OD相交于点E.则下列结论:CBA=;ODBC;OE=AC;四边形AODC是菱形.正确的有 .(填序号)
三、解答题(本大题共4小题,共45分)
如图,AB为O的直径,C,D是O上的两点,且BDOC.求证:=.
如图,点A,B,C是O的三等分点.
(1)求AOB的度数;
(2)若AO=4,求AB的长及ABC的面积.
如图,在⊙O中,弦AD、BC相交于点E,连结OE,已知AD=BC,AD⊥CB.
(1)求证:AB=CD;
(2)如果⊙O的半径为5,DE=1,求AE的长.
15.如图,CD为O的直径,CDAB,垂足为F,AOBC,垂足为E,BC=.
(1)求AB的长;
(2)求O的半径.
1.【答案】B
2.【答案】B
3.【答案】C
4.【答案】C
5.【答案】B
6.【答案】B
7.【答案】
8.【答案】=
9.【答案】
10.【答案】
11.【答案】
12.【答案】证明:OB=OD,
D=B.
BDOC,
D=COD,AOC=B.
AOC=COD.
=.
13.【答案】解:(1)如图,连接OC.
点A,B,C是O的三等分点,
==.
AOB=BOC=AOC==.
(2)如图,过点O作ODAB于点D,
则ODB=,BD=AB.
OA=OB,
OAB=OBA=(-AOB)=.
在RtBOD中,OBA=,
OD=OB=2.
BD===2.
AB=2BD=4.
OA=OB=OC,AOB=BOC=AOC,
AOBBOCAOC.
==.
==3ABOD=42=12.
14.【答案】(1)证明:如图,∵AD=BC,
∴=,
∴-=-,即=
∴AB=CD;
(2)解:如图,过O作OF⊥AD于点F,作OG⊥BC于点G,连接OA、OC.
则AF=FD,BG=CG.
∵AD=BC,
∴AF=CG.
在Rt△AOF与Rt△COG中,
,
∴Rt△AOF≌Rt△COG(HL),
∴OF=OG,
∴四边形OFEG是正方形,
∴OF=EF.
设OF=EF=x,则AF=FD=x+1,
在直角△OAF中.由勾股定理得到:x2+(x+1)2=52,
解得 x=3.
则AF=3+1=4,即AE=AF+3=7.
15.【答案】解:(1)连接AC,
CD为O的直径,CDAB,
=.
AC=BC.
又AOBC,
=.
AC=AB.AB=BC=2.
(2)由(1)知AB=BC=AC,
ABC为等边三角形.
B=.
OAF=.
CDAB,
AF=BF=,OF=AO.
在RtOAF中,=+,即=+,
OA=2,即O的半径为2.
第2页,共3页
同课章节目录
