2021-2022学年人教版九年级数学上册24.1.4 圆周角 同步测试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学上册24.1.4 圆周角 同步测试卷(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 350.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 13:56:29 | ||
图片预览


文档简介
24.1.4 圆周角同步测试卷 2021-2022学年人教版九年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共11小题,共33分)
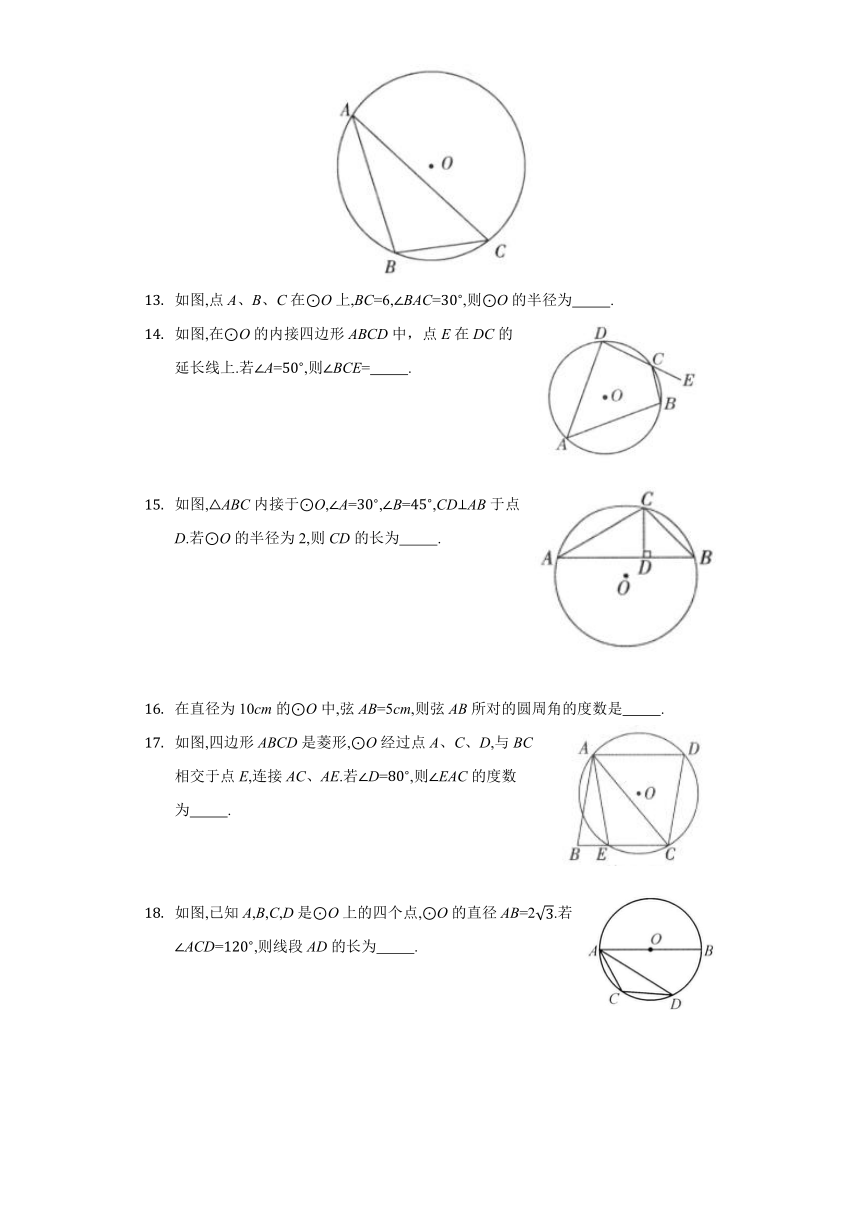
下列图形中的角是圆周角的是( )
A. B. C. D.
如图,E,F,G为圆上的三点,FEG=,P点可能是圆心的是( )
A. B. C. D.
如图,在O中,所对的圆周角ACB=.若P为上一点,AOP=,则POB的度数为( )
A. B.
C. D.
在圆内接四边形ABCD中,若A:B:C=4:3:5,则D的度数是( )
A. B. C. D.
在数学实践活动课中,小辉利用自己制作的一把“直角角尺”测量、计算一些圆的直径.如图,AOB=,将点O放在圆周上,分别确定OA,OB与圆的交点C,D,读得数据OC=8,OD=9,则此圆的直径约为( )
A. B. C. D.
如图,点A,B,S在圆上.若弦AB的长度等于圆半径的倍,则ASB的度数是( )
A. B.
C. D.
有下列命题:圆内接平行四边形是矩形;圆内接矩形是正方形;圆内接菱形是正方形.其中,真命题是( )
A. B. C. D.
如图,AB是半圆的直径,C、D是半圆上的两点,ADC=,则CAB的度数为( )
A. B.
C. D.
如图,在O中,四边形OABC为菱形,点D在上,则ADC的度数为( )
A. B.
C. D.
如图,四边形ABCD是O的内接四边形,BC=DC,BCD=2BAD,BD=8,则O的半径是( )
A. B.
C. D.
如图,A,B,C,D是O上的四个点,B是的中点,M是半径OD上任意一点,若BDC=,则AMB的度数不可能是( )
A. B. C. D.
二、填空题(本大题共10小题,共30分)
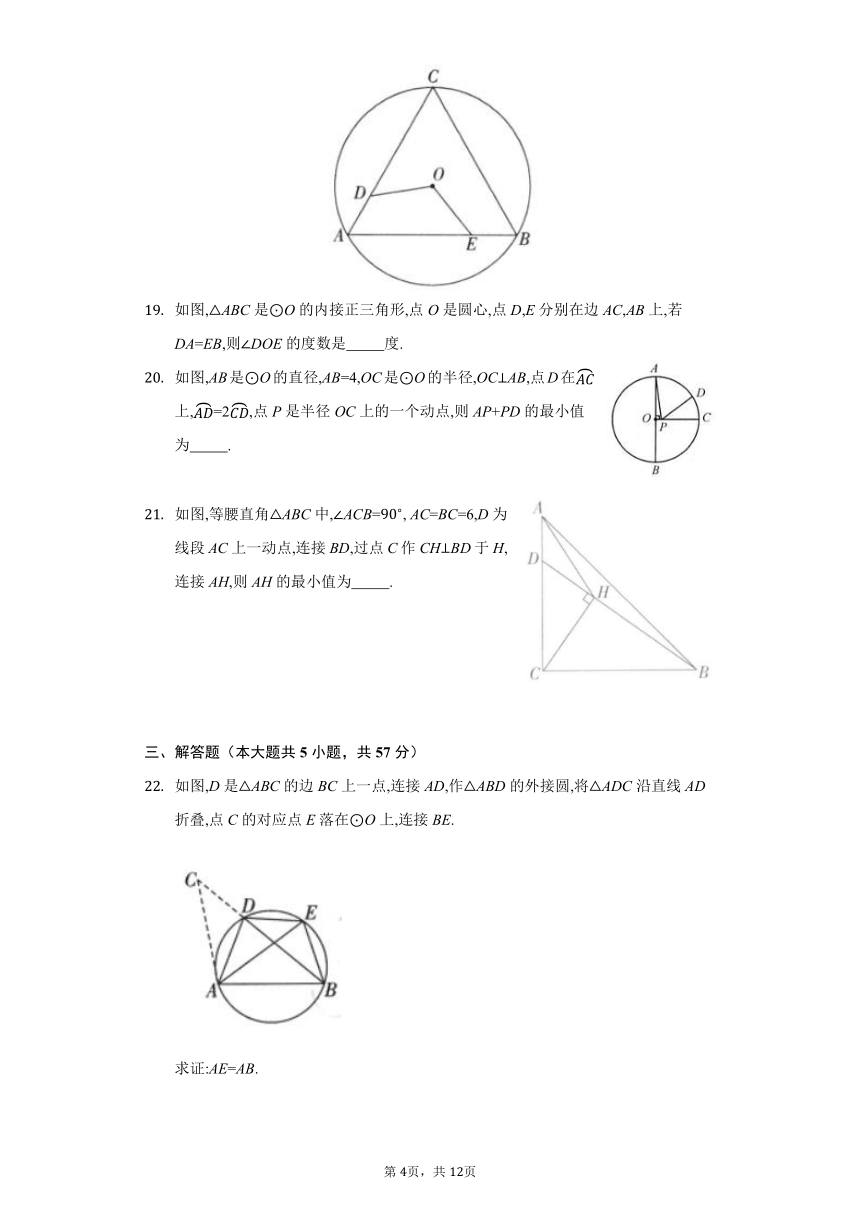
如图,点A、B、C在O上,ACB=,则ABO的度数为 .
如图,点A、B、C在O上,BC=6,BAC=,则O的半径为 .
如图,在O的内接四边形ABCD中,点E在DC的延长线上.若A=,则BCE= .
如图,ABC内接于O,A=,B=,CDAB于点D.若O的半径为2,则CD的长为 .
在直径为10cm的O中,弦AB=5cm,则弦AB所对的圆周角的度数是 .
如图,四边形ABCD是菱形,O经过点A、C、D,与BC相交于点E,连接AC、AE.若D=,则EAC的度数为 .
如图,已知A,B,C,D是O上的四个点,O的直径AB=2.若ACD=,则线段AD的长为 .
如图,ABC是O的内接正三角形,点O是圆心,点D,E分别在边AC,AB上,若DA=EB,则DOE的度数是 度.
如图,AB是O的直径,AB=4,OC是O的半径,OCAB,点D在上,=2,点P是半径OC上的一个动点,则AP+PD的最小值为 .
如图,等腰直角ABC中,ACB=, AC=BC=6,D为线段AC上一动点,连接BD,过点C作CHBD于H,连接AH,则AH的最小值为 .
三、解答题(本大题共5小题,共57分)
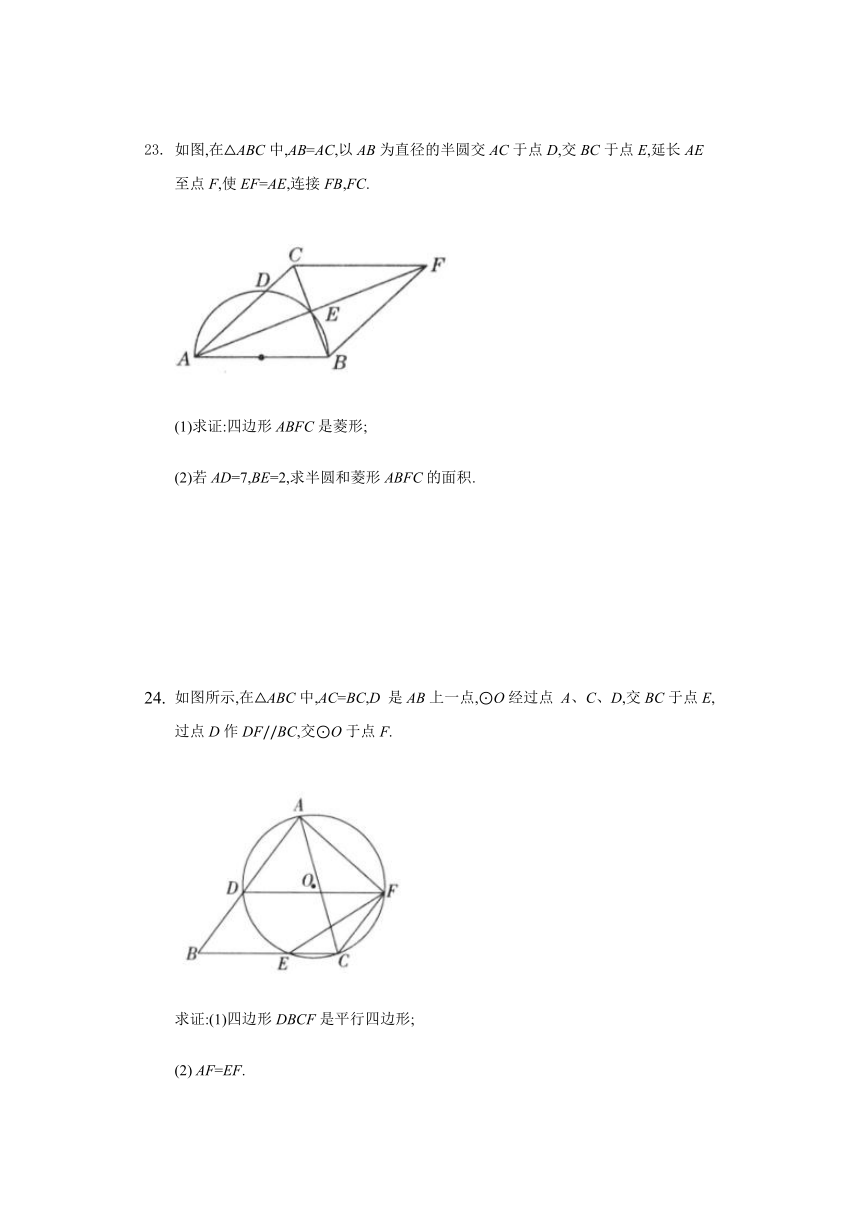
如图,D是ABC的边BC上一点,连接AD,作ABD的外接圆,将ADC沿直线AD折叠,点C的对应点E落在O上,连接BE.
求证:AE=AB.
如图,在ABC中,AB=AC,以AB为直径的半圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.
(1)求证:四边形ABFC是菱形;
(2)若AD=7,BE=2,求半圆和菱形ABFC的面积.
如图所示,在ABC中,AC=BC,D 是AB上一点,O经过点 A、C、D,交BC于点E,过点D作DFBC,交O于点F.
求证:(1)四边形DBCF是平行四边形;
(2) AF=EF.
如图,四边形ABCD内接于O,ABC=,对角线DB平分ADC.
(1)求证:ABC是等边三角形;
(2)若AD=2,DC=3,求ABC的周长.
如图,在四边形ABCD中,AD=BC,B=D,AD不平行于BC,过点C作CEAD,交ABC的外接圆O于点E,连接AE.
(1)求证:四边形AECD为平行四边形;
(2)连接CO,求证:CO平分BCE.
1.【答案】B
2.【答案】C
3.【答案】B
4.【答案】D
5.【答案】C
6.【答案】C
7.【答案】D
8.【答案】C
9.【答案】C
10.【答案】D
11.【答案】D
12.【答案】
13.【答案】6
14.【答案】
15.【答案】
16.【答案】或
17.【答案】
18.【答案】3
19.【答案】120
20.【答案】2
21.【答案】3-3
22.【答案】解:由折叠的性质,可知ADEADC,
AED=C, AE=AC.
=,ABD=AED.
ABD= C.AB=AC.
AE=AB.
23.【答案】(1)证明:AB是直径,
AEB=.
AEBC.
AB=AC,
BE=CE.
AE=EF,
四边形ABFC是平行四边形.
AC=AB,
四边形ABFC是菱形.
(2)解:设CD=x,则AB=AC=7+x.
由(1)知BC=2BE=4.
如图,连接BD.
AB是半圆的直径,
ADB=.
∴BDC=90°
-=-.
-=-.
解得x=1或x=-8(舍去).
AB=8.
BD==,
==8.
==8.
24.【答案】证明:(1)AC=BC,
BAC=B,
DFBC,
ADF=B,
BAC=CFD,
ADF=CFD,
BDCF,
DFBC,
四边形DBCF是平行四边形.
(2)连接AE,
DFBC,
ADF=B,
又ADF=AEF,
AEF=B,
四边形AECF是O的内接四边形,
ECF+EAF=,
BDCF,
ECF+B=,
EAF=B,
AEF=EAF,
AF=EF.
25.【答案】解:(1)∵四边形ABCD内接于O,
ABC+ADC=
∠ABC=,
ADC=.
DB平分ADC,
ADB=CDB=.
=,=,
ACB=ADB=,BAC=CDB=.
ABC=ACB=BAC.
ABC是等边三角形
(2)如图,过点A作AMCD,交CD的延长线于点M,
AMD=.
ADC=,MDC=,
ADM=
在RtAMD中,DAM=.
DM=AD=1.
AM==.
CD=3,CM=CD+DM=4.
在RtAMC中,AC==.
ABC是等边三角形,
AB=AC=BC=.
ABC的周长为3
26.【答案】解:(1)=,B=E.
B=D,E=D.
CEAD,D+ECD=.E+ECD=.
AECD.四边形AECD为平行四边形
(2)如图,连接OE、OB.
四边形AECD为平行四边形,AD=EC.
AD=BC,EC=BC.
又OC=OC,OE=OB,COECOB.
OCE=OCB,即CO平分BCE
第2页,共3页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共11小题,共33分)
下列图形中的角是圆周角的是( )
A. B. C. D.
如图,E,F,G为圆上的三点,FEG=,P点可能是圆心的是( )
A. B. C. D.
如图,在O中,所对的圆周角ACB=.若P为上一点,AOP=,则POB的度数为( )
A. B.
C. D.
在圆内接四边形ABCD中,若A:B:C=4:3:5,则D的度数是( )
A. B. C. D.
在数学实践活动课中,小辉利用自己制作的一把“直角角尺”测量、计算一些圆的直径.如图,AOB=,将点O放在圆周上,分别确定OA,OB与圆的交点C,D,读得数据OC=8,OD=9,则此圆的直径约为( )
A. B. C. D.
如图,点A,B,S在圆上.若弦AB的长度等于圆半径的倍,则ASB的度数是( )
A. B.
C. D.
有下列命题:圆内接平行四边形是矩形;圆内接矩形是正方形;圆内接菱形是正方形.其中,真命题是( )
A. B. C. D.
如图,AB是半圆的直径,C、D是半圆上的两点,ADC=,则CAB的度数为( )
A. B.
C. D.
如图,在O中,四边形OABC为菱形,点D在上,则ADC的度数为( )
A. B.
C. D.
如图,四边形ABCD是O的内接四边形,BC=DC,BCD=2BAD,BD=8,则O的半径是( )
A. B.
C. D.
如图,A,B,C,D是O上的四个点,B是的中点,M是半径OD上任意一点,若BDC=,则AMB的度数不可能是( )
A. B. C. D.
二、填空题(本大题共10小题,共30分)
如图,点A、B、C在O上,ACB=,则ABO的度数为 .
如图,点A、B、C在O上,BC=6,BAC=,则O的半径为 .
如图,在O的内接四边形ABCD中,点E在DC的延长线上.若A=,则BCE= .
如图,ABC内接于O,A=,B=,CDAB于点D.若O的半径为2,则CD的长为 .
在直径为10cm的O中,弦AB=5cm,则弦AB所对的圆周角的度数是 .
如图,四边形ABCD是菱形,O经过点A、C、D,与BC相交于点E,连接AC、AE.若D=,则EAC的度数为 .
如图,已知A,B,C,D是O上的四个点,O的直径AB=2.若ACD=,则线段AD的长为 .
如图,ABC是O的内接正三角形,点O是圆心,点D,E分别在边AC,AB上,若DA=EB,则DOE的度数是 度.
如图,AB是O的直径,AB=4,OC是O的半径,OCAB,点D在上,=2,点P是半径OC上的一个动点,则AP+PD的最小值为 .
如图,等腰直角ABC中,ACB=, AC=BC=6,D为线段AC上一动点,连接BD,过点C作CHBD于H,连接AH,则AH的最小值为 .
三、解答题(本大题共5小题,共57分)
如图,D是ABC的边BC上一点,连接AD,作ABD的外接圆,将ADC沿直线AD折叠,点C的对应点E落在O上,连接BE.
求证:AE=AB.
如图,在ABC中,AB=AC,以AB为直径的半圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.
(1)求证:四边形ABFC是菱形;
(2)若AD=7,BE=2,求半圆和菱形ABFC的面积.
如图所示,在ABC中,AC=BC,D 是AB上一点,O经过点 A、C、D,交BC于点E,过点D作DFBC,交O于点F.
求证:(1)四边形DBCF是平行四边形;
(2) AF=EF.
如图,四边形ABCD内接于O,ABC=,对角线DB平分ADC.
(1)求证:ABC是等边三角形;
(2)若AD=2,DC=3,求ABC的周长.
如图,在四边形ABCD中,AD=BC,B=D,AD不平行于BC,过点C作CEAD,交ABC的外接圆O于点E,连接AE.
(1)求证:四边形AECD为平行四边形;
(2)连接CO,求证:CO平分BCE.
1.【答案】B
2.【答案】C
3.【答案】B
4.【答案】D
5.【答案】C
6.【答案】C
7.【答案】D
8.【答案】C
9.【答案】C
10.【答案】D
11.【答案】D
12.【答案】
13.【答案】6
14.【答案】
15.【答案】
16.【答案】或
17.【答案】
18.【答案】3
19.【答案】120
20.【答案】2
21.【答案】3-3
22.【答案】解:由折叠的性质,可知ADEADC,
AED=C, AE=AC.
=,ABD=AED.
ABD= C.AB=AC.
AE=AB.
23.【答案】(1)证明:AB是直径,
AEB=.
AEBC.
AB=AC,
BE=CE.
AE=EF,
四边形ABFC是平行四边形.
AC=AB,
四边形ABFC是菱形.
(2)解:设CD=x,则AB=AC=7+x.
由(1)知BC=2BE=4.
如图,连接BD.
AB是半圆的直径,
ADB=.
∴BDC=90°
-=-.
-=-.
解得x=1或x=-8(舍去).
AB=8.
BD==,
==8.
==8.
24.【答案】证明:(1)AC=BC,
BAC=B,
DFBC,
ADF=B,
BAC=CFD,
ADF=CFD,
BDCF,
DFBC,
四边形DBCF是平行四边形.
(2)连接AE,
DFBC,
ADF=B,
又ADF=AEF,
AEF=B,
四边形AECF是O的内接四边形,
ECF+EAF=,
BDCF,
ECF+B=,
EAF=B,
AEF=EAF,
AF=EF.
25.【答案】解:(1)∵四边形ABCD内接于O,
ABC+ADC=
∠ABC=,
ADC=.
DB平分ADC,
ADB=CDB=.
=,=,
ACB=ADB=,BAC=CDB=.
ABC=ACB=BAC.
ABC是等边三角形
(2)如图,过点A作AMCD,交CD的延长线于点M,
AMD=.
ADC=,MDC=,
ADM=
在RtAMD中,DAM=.
DM=AD=1.
AM==.
CD=3,CM=CD+DM=4.
在RtAMC中,AC==.
ABC是等边三角形,
AB=AC=BC=.
ABC的周长为3
26.【答案】解:(1)=,B=E.
B=D,E=D.
CEAD,D+ECD=.E+ECD=.
AECD.四边形AECD为平行四边形
(2)如图,连接OE、OB.
四边形AECD为平行四边形,AD=EC.
AD=BC,EC=BC.
又OC=OC,OE=OB,COECOB.
OCE=OCB,即CO平分BCE
第2页,共3页
同课章节目录
