2021-2022学年人教版九年级数学上册24.2.1 点和圆的位置关系同步测试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学上册24.2.1 点和圆的位置关系同步测试卷(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 129.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 00:00:00 | ||
图片预览

文档简介
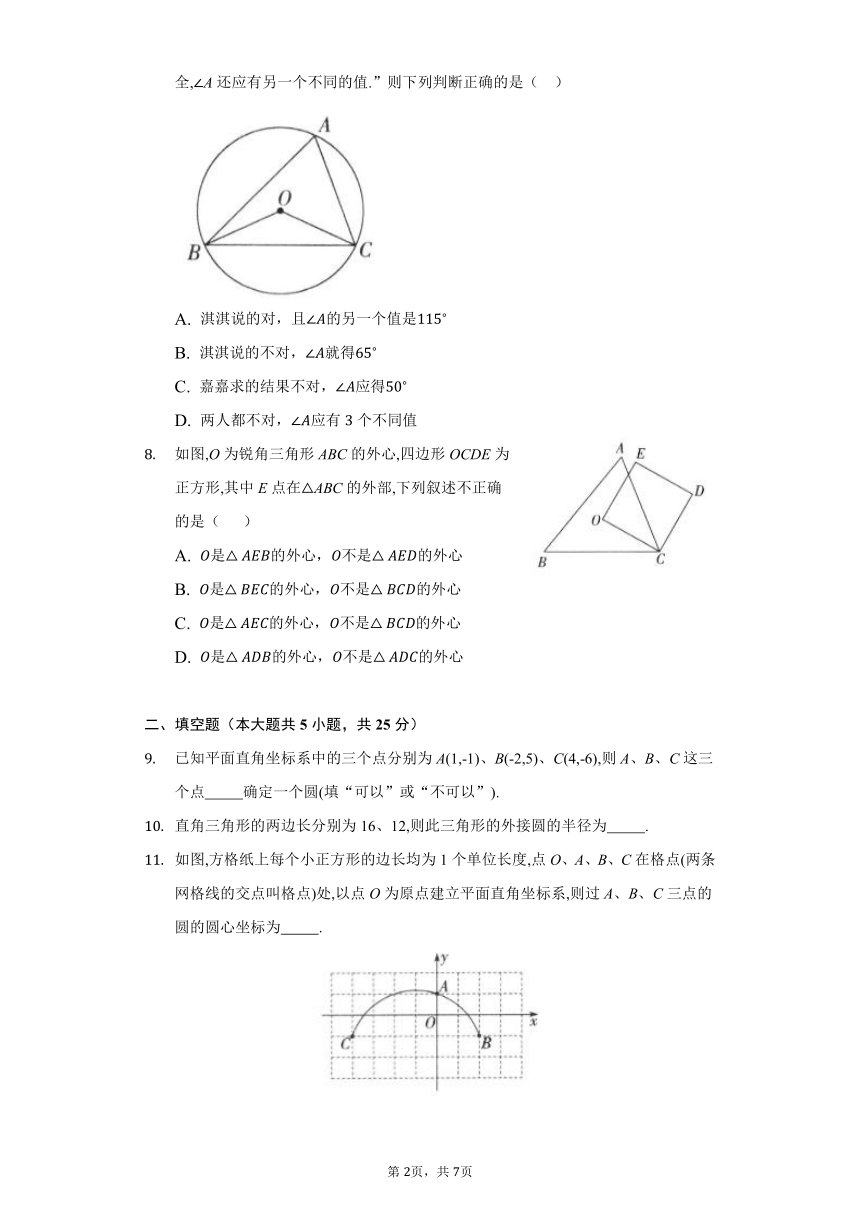
24.2 点和圆的位置关系同步测试卷 2021-2022学年人教版九年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共8小题,共40分)
已知O的半径为5,点P在O内,则下列关系正确的是( )
A. B. C. D. 无法判断
下列关于确定一个圆的说法中,正确的是( )
A. 三个点一定能确定一个圆 B. 以已知线段为半径能确定一个圆
C. 以已知线段为直径能确定一个圆 D. 菱形的四个顶点能确定一个圆
根据圆规作图的痕迹,可用直尺成功找到三角形外心的是( )
A. B.
C. D.
已知点A、B,且AB<4,则经过A、B两点且半径为2的圆有( )
A. 个 B. 个 C. 个 D. 无数个
边长为2的正三角形的外接圆的半径是( )
A. B. C. D.
如图,在ABC中,AB=AC,AD是BAC的平分线,EF是AC的垂直平分线,交AD于点O.若OA=3,则ABC的外接圆的面积为( )
A. B.
C. D.
有一题目:“已知:点O为ABC的外心,BOC=,求A.”嘉嘉的解答:画ABC以及它的外接圆O,连接OB,OC,如图,由BOC=2A=,得A=,而淇淇说:“嘉嘉考虑的不周全,A还应有另一个不同的值.”则下列判断正确的是( )
A. 淇淇说的对,且的另一个值是
B. 淇淇说的不对,就得
C. 嘉嘉求的结果不对,应得
D. 两人都不对,应有个不同值
如图,O为锐角三角形ABC的外心,四边形OCDE为正方形,其中E点在ABC的外部,下列叙述不正确的是( )
A. 是的外心,不是的外心
B. 是的外心,不是的外心
C. 是的外心,不是的外心
D. 是的外心,不是的外心
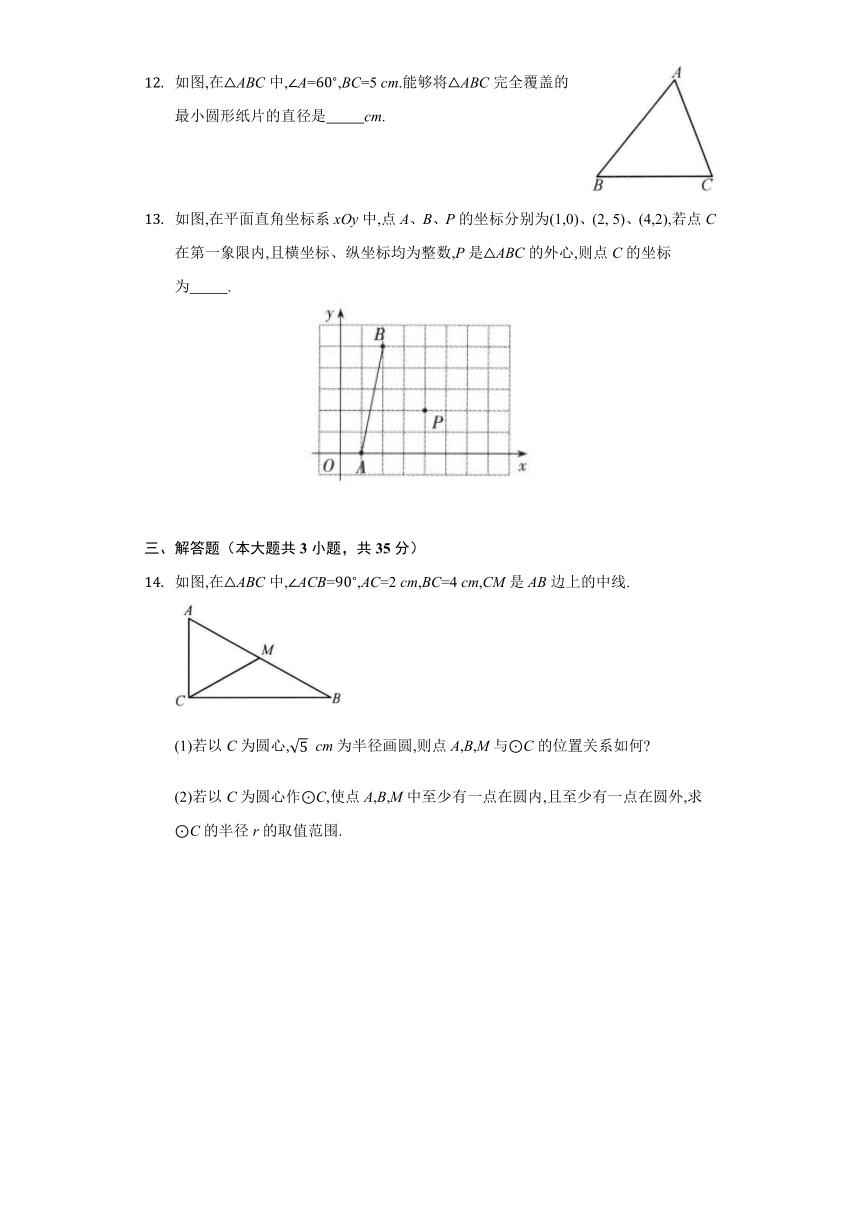
二、填空题(本大题共5小题,共25分)
已知平面直角坐标系中的三个点分别为A(1,-1)、B(-2,5)、C(4,-6),则A、B、C这三个点 确定一个圆(填“可以”或“不可以”).
直角三角形的两边长分别为16、12,则此三角形的外接圆的半径为 .
如图,方格纸上每个小正方形的边长均为1个单位长度,点O、A、B、C在格点(两条网格线的交点叫格点)处,以点O为原点建立平面直角坐标系,则过A、B、C三点的圆的圆心坐标为 .
如图,在ABC中,A=,BC=5 cm.能够将ABC完全覆盖的最小圆形纸片的直径是 cm.
如图,在平面直角坐标系xOy中,点A、B、P的坐标分别为(1,0)、(2, 5)、(4,2),若点C在第一象限内,且横坐标、纵坐标均为整数,P是ABC的外心,则点C的坐标为 .
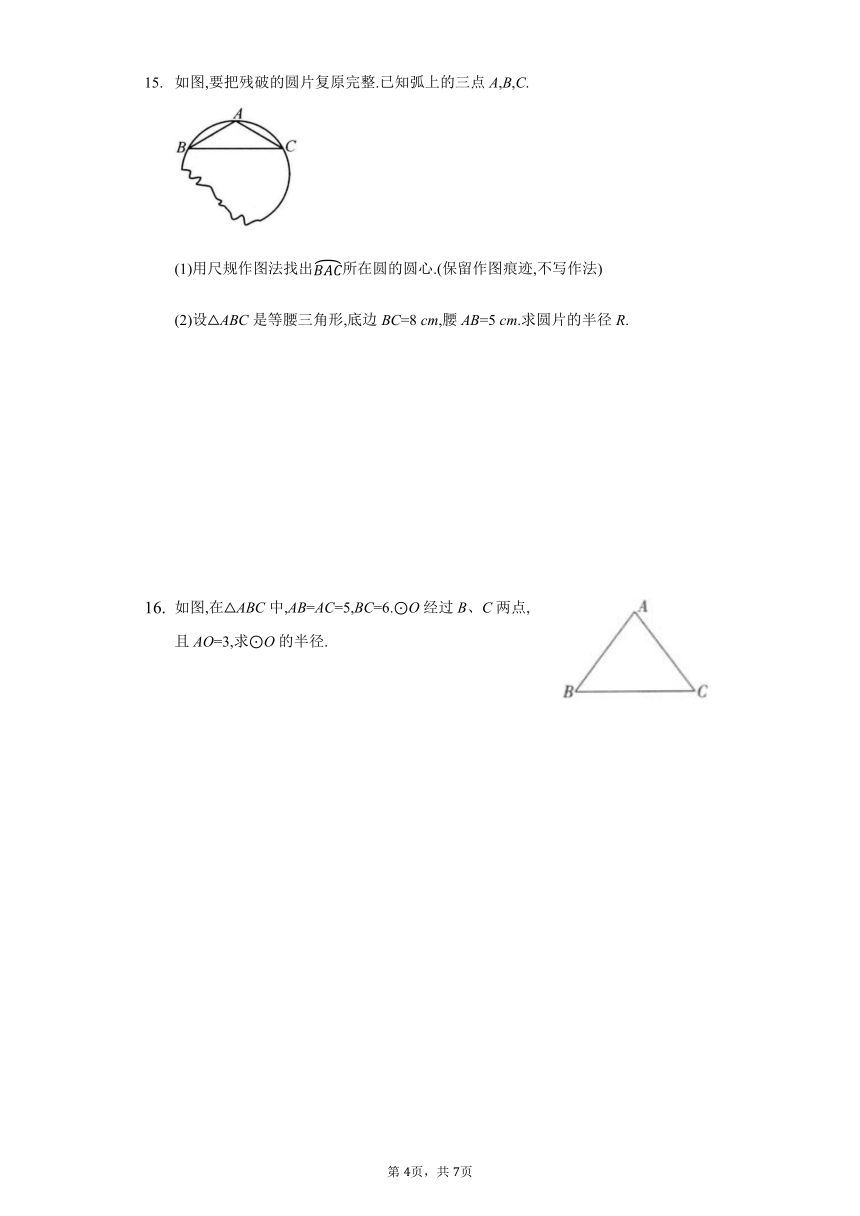
三、解答题(本大题共3小题,共35分)
如图,在ABC中,ACB=,AC=2 cm,BC=4 cm,CM是AB边上的中线.
(1)若以C为圆心, cm为半径画圆,则点A,B,M与C的位置关系如何
(2)若以C为圆心作C,使点A,B,M中至少有一点在圆内,且至少有一点在圆外,求C的半径r的取值范围.
如图,要把残破的圆片复原完整.已知弧上的三点A,B,C.
(1)用尺规作图法找出所在圆的圆心.(保留作图痕迹,不写作法)
(2)设ABC是等腰三角形,底边BC=8 cm,腰AB=5 cm.求圆片的半径R.
如图,在ABC中,AB=AC=5,BC=6.O经过B、C两点,且AO=3,求O的半径.
1.【答案】B
2.【答案】C
3.【答案】C
4.【答案】C
5.【答案】C
6.【答案】D
7.【答案】A
8.【答案】D
9.【答案】可以
10.【答案】10或8
11.【答案】(-1,-2)
12.【答案】
13.【答案】 (7,4)或(1,4)或(6,5)
14.【答案】解:(1)CA=2 cm< cm,
点A在C内.
BC=4 cm> cm,
点B在C外.
由勾股定理,得AB==2 cm,
CM是AB边上的中线,
CM=AB= cm.
点M在C上.
(2)当点B在圆上时,r=4 cm,
当点A在圆上时,r=2 cm,
当点M在圆上时,r= cm,
故满足题意的r的取值范围是2 cm< r<4 cm.
15.【答案】解:(1)分别作AB,AC的垂直平分线,设交点为O,则点O为所求圆的圆心.
(2)连接AO交BC于点E.
AB=AC,
=.
OABC,BE=BC=4.
在RtABE中,AE===3.
连接OB,
在RtBEO中,=+.
即=+,解得R=.
所求圆片的半径R为 cm.
16.【答案】解:如图,过点A作ADBC,垂足为D.
AB=AC=5, ADBC,BC=6,易得点O在直线AD上,BD=BC=3.
在RtABD中,AD==4.
当点在射线AD的反向延长线上时,连接.
=AD+=4+3=7,在Rt中,===.
当点在线段AD上时,连接.
=AD-=4-3=1,在Rt中,===.
综上所述,O的半径为或.
第2页,共3页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共8小题,共40分)
已知O的半径为5,点P在O内,则下列关系正确的是( )
A. B. C. D. 无法判断
下列关于确定一个圆的说法中,正确的是( )
A. 三个点一定能确定一个圆 B. 以已知线段为半径能确定一个圆
C. 以已知线段为直径能确定一个圆 D. 菱形的四个顶点能确定一个圆
根据圆规作图的痕迹,可用直尺成功找到三角形外心的是( )
A. B.
C. D.
已知点A、B,且AB<4,则经过A、B两点且半径为2的圆有( )
A. 个 B. 个 C. 个 D. 无数个
边长为2的正三角形的外接圆的半径是( )
A. B. C. D.
如图,在ABC中,AB=AC,AD是BAC的平分线,EF是AC的垂直平分线,交AD于点O.若OA=3,则ABC的外接圆的面积为( )
A. B.
C. D.
有一题目:“已知:点O为ABC的外心,BOC=,求A.”嘉嘉的解答:画ABC以及它的外接圆O,连接OB,OC,如图,由BOC=2A=,得A=,而淇淇说:“嘉嘉考虑的不周全,A还应有另一个不同的值.”则下列判断正确的是( )
A. 淇淇说的对,且的另一个值是
B. 淇淇说的不对,就得
C. 嘉嘉求的结果不对,应得
D. 两人都不对,应有个不同值
如图,O为锐角三角形ABC的外心,四边形OCDE为正方形,其中E点在ABC的外部,下列叙述不正确的是( )
A. 是的外心,不是的外心
B. 是的外心,不是的外心
C. 是的外心,不是的外心
D. 是的外心,不是的外心
二、填空题(本大题共5小题,共25分)
已知平面直角坐标系中的三个点分别为A(1,-1)、B(-2,5)、C(4,-6),则A、B、C这三个点 确定一个圆(填“可以”或“不可以”).
直角三角形的两边长分别为16、12,则此三角形的外接圆的半径为 .
如图,方格纸上每个小正方形的边长均为1个单位长度,点O、A、B、C在格点(两条网格线的交点叫格点)处,以点O为原点建立平面直角坐标系,则过A、B、C三点的圆的圆心坐标为 .
如图,在ABC中,A=,BC=5 cm.能够将ABC完全覆盖的最小圆形纸片的直径是 cm.
如图,在平面直角坐标系xOy中,点A、B、P的坐标分别为(1,0)、(2, 5)、(4,2),若点C在第一象限内,且横坐标、纵坐标均为整数,P是ABC的外心,则点C的坐标为 .
三、解答题(本大题共3小题,共35分)
如图,在ABC中,ACB=,AC=2 cm,BC=4 cm,CM是AB边上的中线.
(1)若以C为圆心, cm为半径画圆,则点A,B,M与C的位置关系如何
(2)若以C为圆心作C,使点A,B,M中至少有一点在圆内,且至少有一点在圆外,求C的半径r的取值范围.
如图,要把残破的圆片复原完整.已知弧上的三点A,B,C.
(1)用尺规作图法找出所在圆的圆心.(保留作图痕迹,不写作法)
(2)设ABC是等腰三角形,底边BC=8 cm,腰AB=5 cm.求圆片的半径R.
如图,在ABC中,AB=AC=5,BC=6.O经过B、C两点,且AO=3,求O的半径.
1.【答案】B
2.【答案】C
3.【答案】C
4.【答案】C
5.【答案】C
6.【答案】D
7.【答案】A
8.【答案】D
9.【答案】可以
10.【答案】10或8
11.【答案】(-1,-2)
12.【答案】
13.【答案】 (7,4)或(1,4)或(6,5)
14.【答案】解:(1)CA=2 cm< cm,
点A在C内.
BC=4 cm> cm,
点B在C外.
由勾股定理,得AB==2 cm,
CM是AB边上的中线,
CM=AB= cm.
点M在C上.
(2)当点B在圆上时,r=4 cm,
当点A在圆上时,r=2 cm,
当点M在圆上时,r= cm,
故满足题意的r的取值范围是2 cm< r<4 cm.
15.【答案】解:(1)分别作AB,AC的垂直平分线,设交点为O,则点O为所求圆的圆心.
(2)连接AO交BC于点E.
AB=AC,
=.
OABC,BE=BC=4.
在RtABE中,AE===3.
连接OB,
在RtBEO中,=+.
即=+,解得R=.
所求圆片的半径R为 cm.
16.【答案】解:如图,过点A作ADBC,垂足为D.
AB=AC=5, ADBC,BC=6,易得点O在直线AD上,BD=BC=3.
在RtABD中,AD==4.
当点在射线AD的反向延长线上时,连接.
=AD+=4+3=7,在Rt中,===.
当点在线段AD上时,连接.
=AD-=4-3=1,在Rt中,===.
综上所述,O的半径为或.
第2页,共3页
同课章节目录
