2021-2022学年苏科版九年级数学上册2.7弧长与扇形的面积巩固练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版九年级数学上册2.7弧长与扇形的面积巩固练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 459.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 00:00:00 | ||
图片预览


文档简介
2.7弧长与扇形的面积巩固练习
一、选择题
圆心角为 的扇形的半径为 ,则这个扇形的面积是
A. B. C. D.
若扇形的圆心角为 ,半径为 ,则该扇形的弧长为
A. B. C. D.
已知圆的半径为 ,扇形的圆心角为 ,则扇形的面积为
A. B. C. D.
如图,点 是以 为直径的半圆 的三等分点,,则图中阴影部分的面积是
A. B. C. D.
半径为 的圆在长为 、宽为 的长方形内滚动,则该圆滚动过程中所能覆盖部分的最大面积等于
A. B. C. D.
如图,正六边形 内接于 , 的半径为 ,则这个正六边形的边心距 和 的长分别为
A. , B. , C. , D. ,
如图,已知 的半径是 ,点 ,, 在 上,若四边形 为菱形,则图中阴影部分面积为
A. B. C. D.
如图,扇形 的半径为 ,,以 为直径画半圆,则图中阴影部分的面积为
A. B. C. D.
如图,四边形 是菱形,,,扇形 的半径为 ,圆心角为 ,则图中阴影部分的面积是
A. B. C. D.
如图,在矩形 中,已知 ,,矩形的对角线长为 ,矩形在直线 上绕其右下角的顶点 向右旋转 至图①位置,再绕右下角的顶点继续向右旋转 至图②位置,以此类推,这样连续旋转 次后,顶点 在整个旋转过程中所经过的路程之和是
A. B. C. D.
二、填空题
一条弧所对的圆心角为 ,弧长等于半径为 的圆的周长的 倍,则这条弧的半径为 .
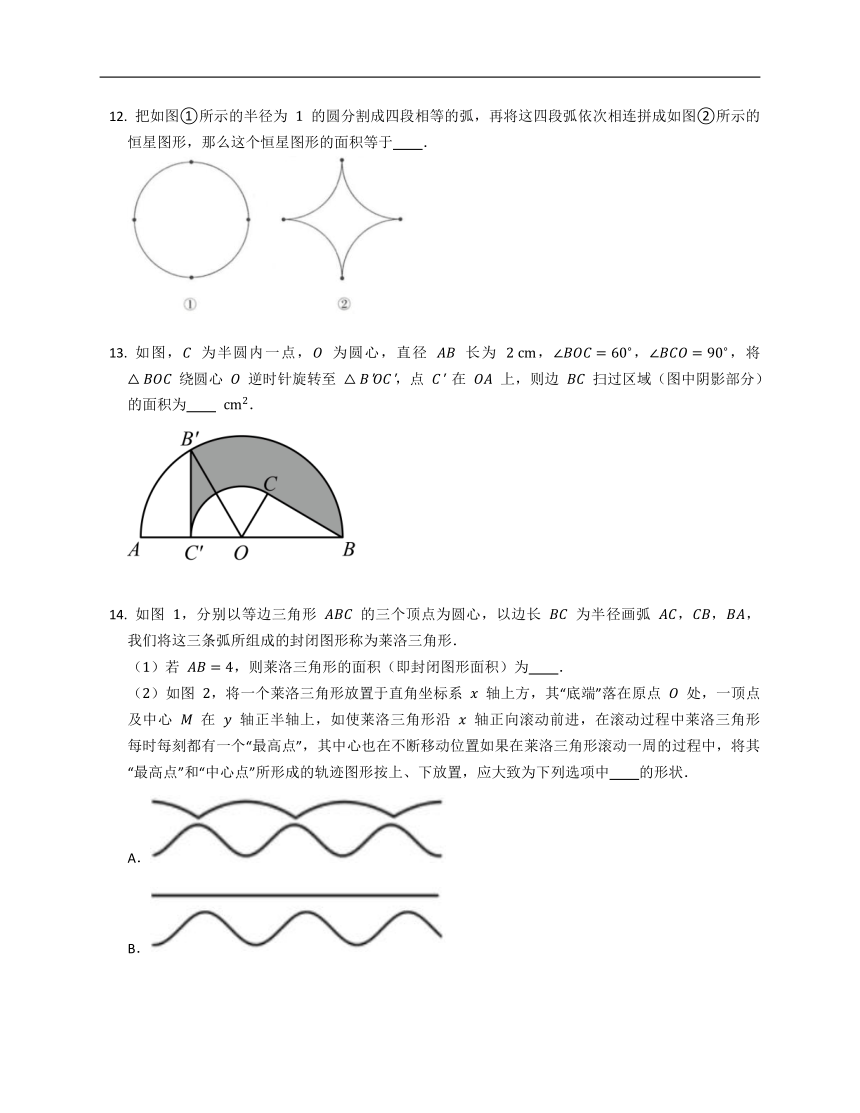
把如图①所示的半径为 的圆分割成四段相等的弧,再将这四段弧依次相连拼成如图②所示的恒星图形,那么这个恒星图形的面积等于 .
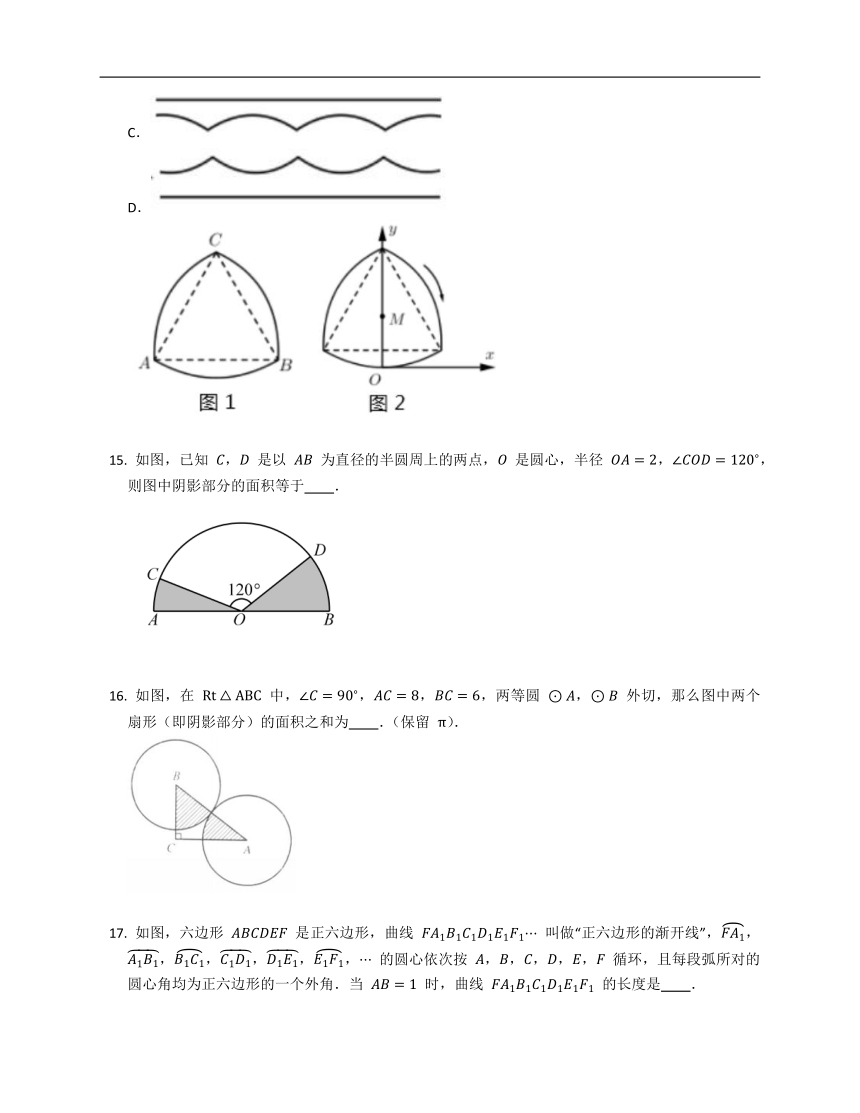
如图, 为半圆内一点, 为圆心,直径 长为 ,,,将 绕圆心 逆时针旋转至 ,点 在 上,则边 扫过区域(图中阴影部分)的面积为 .
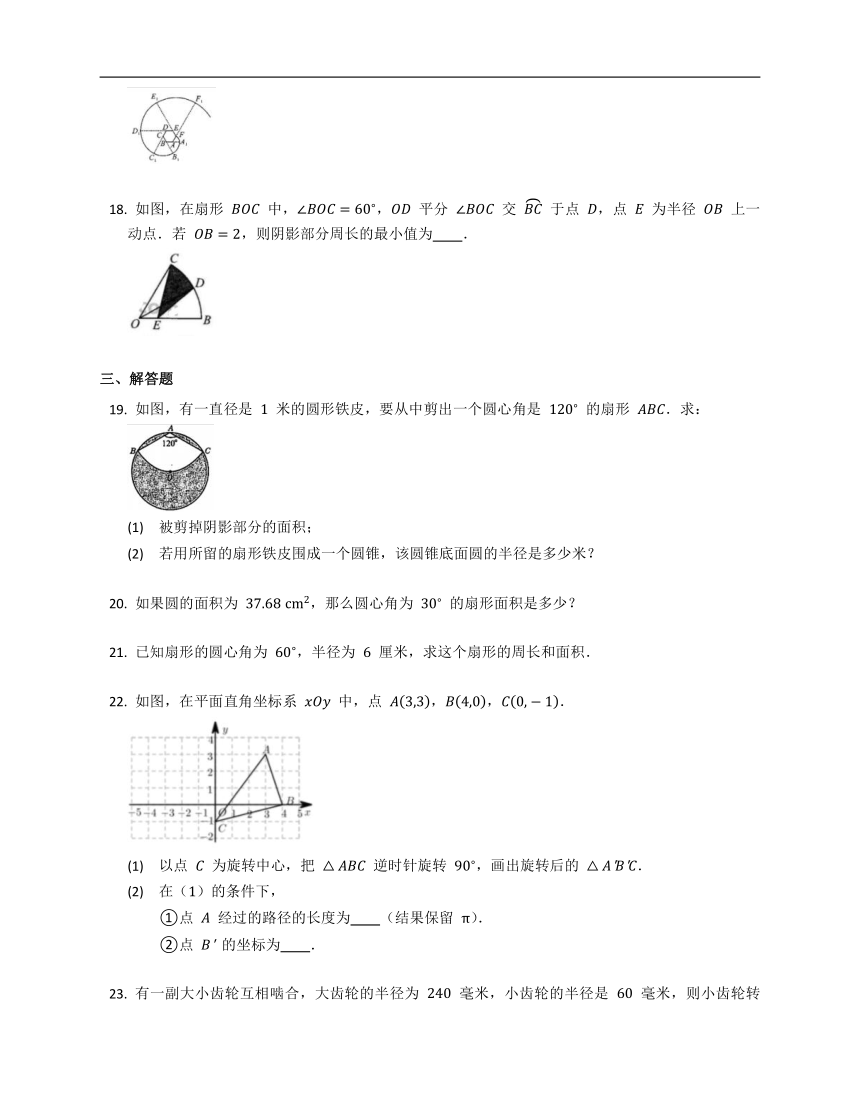
如图 ,分别以等边三角形 的三个顶点为圆心,以边长 为半径画弧 ,,,我们将这三条弧所组成的封闭图形称为莱洛三角形.
()若 ,则莱洛三角形的面积(即封闭图形面积)为 .
()如图 ,将一个莱洛三角形放置于直角坐标系 轴上方,其“底端”落在原点 处,一顶点及中心 在 轴正半轴上,如使莱洛三角形沿 轴正向滚动前进,在滚动过程中莱洛三角形每时每刻都有一个“最高点”,其中心也在不断移动位置如果在莱洛三角形滚动一周的过程中,将其“最高点”和“中心点”所形成的轨迹图形按上、下放置,应大致为下列选项中 的形状.
A.
B.
C.
D.
如图,已知 , 是以 为直径的半圆周上的两点, 是圆心,半径 ,,则图中阴影部分的面积等于 .
如图,在 中,,,,两等圆 , 外切,那么图中两个扇形(即阴影部分)的面积之和为 .(保留 ).
如图,六边形 是正六边形,曲线 叫做“正六边形的渐开线”,,,,,,, 的圆心依次按 ,,,,, 循环,且每段弧所对的圆心角均为正六边形的一个外角.当 时,曲线 的长度是 .
如图,在扇形 中,, 平分 交 于点 ,点 为半径 上一动点.若 ,则阴影部分周长的最小值为 .
三、解答题
如图,有一直径是 米的圆形铁皮,要从中剪出一个圆心角是 的扇形 .求:
(1) 被剪掉阴影部分的面积;
(2) 若用所留的扇形铁皮围成一个圆锥,该圆锥底面圆的半径是多少米?
如果圆的面积为 ,那么圆心角为 的扇形面积是多少?
已知扇形的圆心角为 ,半径为 厘米,求这个扇形的周长和面积.
如图,在平面直角坐标系 中,点 ,,.
(1) 以点 为旋转中心,把 逆时针旋转 ,画出旋转后的 .
(2) 在()的条件下,
①点 经过的路径的长度为 (结果保留 ).
②点 的坐标为 .
有一副大小齿轮互相啮合,大齿轮的半径为 毫米,小齿轮的半径是 毫米,则小齿轮转动一周时,大齿轮转动的角度是多少?
如图,在网格中将 绕点 逆时针旋转 得到 .
(1) 在网格中作出 ;(不要求写作法)
(2) 设网格中小正方形的边长均为 ,求线段 扫过的面积.(结果保留 )
回答下列问题:
(1) 如图,已知线段 上有两点 , 且 ,点 , 分别为 , 的中点, 厘米.求 的长.
(2) 如图,圆 的直径为 ,两条直径 , 相交成 角,, 是 的平分线.
①求 的度数;
②求扇形 的面积.
如图,直线 与双曲线 交于 , 两点,与 , 轴分别交于 , 两点,且 .
(1) 求一次函数和反比例函数解析式;
(2) 若点 与点 关于 轴对称,连接 ,,求 的面积.
如图,在扇形 中,,, 是 的中点, 于点 ,交 于点 ,以 为半径的 交 于点 .求图中涂色部分的面积.
如图,在平面直角坐标系 中, 由 绕点 顺时针旋转得到,且顶点都在格点上.
(1) 点 的坐标为 ,旋转角度为 .
(2) 求点 旋转到 所经过的路线长.
答案
一、选择题(共10题)
1. 【答案】D
【解析】.
【知识点】扇形面积的计算
2. 【答案】C
【知识点】弧长的计算
3. 【答案】C
【解析】 扇形的圆心角为 ,其半径为 ,
.
【知识点】扇形面积的计算
4. 【答案】A
【解析】连接 ,
点 是以 为直径的半圆 的三等分点,
,,
为半圆的直径,
,
,
的面积 的面积 ,
扇形 的面积 ,
则阴影部分的面积 ,故选:A.
【知识点】扇形面积的计算
5. 【答案】B
【知识点】扇形面积的计算
6. 【答案】D
【解析】如图所示,连接 ,,
多边形 是正六边形,
,
,
是等边三角形,
,
,
的长 .
【知识点】弧长的计算
7. 【答案】B
【解析】连接 和 交于点 ,如图所示:
圆的半径为 ,
,
又四边形 是菱形,
,,
在 中,利用勾股定理可知:,,
,
,,
,
,
则图中阴影部分面积为 .
【知识点】扇形面积的计算
8. 【答案】C
【知识点】扇形面积的计算
9. 【答案】A
【解析】连接 .
四边形 是菱形,,
,
,
是等边三角形,
,
的高为 ,
扇形 的半径为 ,圆心角为 ,
,,
,
设 , 相交于点 ,设 , 相交于点 ,
在 和 中,
,
四边形 的面积等于 的面积,
图中阴影部分的面积是:.
【知识点】扇形面积的计算、菱形的性质
10. 【答案】D
【知识点】弧长的计算
二、填空题(共8题)
11. 【答案】
【知识点】弧长的计算
12. 【答案】
【解析】如图,
新的正方形的边长为 ,
恒星图形的面积 ,
故答案为 .
【知识点】扇形面积的计算
13. 【答案】
【解析】 , 是 绕圆心 逆时针旋转得到的,
,,
,,
,
,
,
,,
,.
【知识点】扇形面积的计算
14. 【答案】 ;B
【解析】()过 作 于 ,
因为 是等边三角形,
所以 ,,
因为 ,
所以 ,,
所以 的面积为 ,
,
所以莱洛三角形的面积 .
故答案为:.
()由题意,最高点到 轴的距离是不变的,中心点 到 轴的距离开始是增加然后减小,再增加,又减小,不断循环.
故图象选B.
故选B.
【知识点】弧长的计算
15. 【答案】
【解析】
答:图中阴影部分的面积等于 .
【知识点】扇形面积的计算
16. 【答案】
【知识点】扇形面积的计算、圆与圆的位置关系
17. 【答案】
【知识点】弧长的计算
18. 【答案】
【知识点】弧长的计算、找动点,使距离之和最小
三、解答题(共10题)
19. 【答案】
(1) 连接 ,,,
,,
.
又 ,
,
是等边三角形,
米,
(平方米),
(平方米).
(2) 在扇形 中, 的长为 (米).
设底面圆的半径为 米,则 ,
,
该圆锥底面圆的半径是 米.
【知识点】扇形面积的计算、图形初步、圆锥的表面积计算
20. 【答案】 .
【知识点】扇形面积的计算
21. 【答案】 厘米, 平方厘米.
【知识点】弧长的计算、扇形面积的计算
22. 【答案】
(1) 如图所示, 即为所求.
(2) ;
【解析】
(2) ① ,,
点 经过的路径的长为 ,
故答案为:.
②由图知点 的坐标为 .
故答案为:.
【知识点】坐标平面内图形的旋转变换、弧长的计算、勾股定理
23. 【答案】 .
【知识点】弧长的计算
24. 【答案】
(1) 如答图 所示.
(2) 由题意得 ,则线段 扫过的面积为 .
【知识点】扇形面积的计算、作图-旋转变换
25. 【答案】
(1) ,
设 ,,,
, 分别是 , 的中点,
,
,
,
.
(2) ① ,,
,
是 的平分线,
,
两条直径 , 相交成 角,
;
② 的面积 ,
扇形 的面积 .
【知识点】扇形面积的计算、线段的和差、角的计算
26. 【答案】
(1) ,
,
,
,
,
把 , 分别代入 ,得
解得
一次函数的解析式为 ,
把 代入 ,得 ,
.
把 代入 ,得 ,
反比例函数的解析式为 .
(2) 点 与点 关于 轴对称,由()知 ,
,
,
解方程组 得
,
,
,
【知识点】一次函数的解析式、坐标平面内图形的面积、反比例函数的解析式、反比例函数与方程、不等式
27. 【答案】如图,连接 ,,
,
,
为 的中点,,
,,
,
为等边三角形,
,
在 中,由勾股定理,得 ,
【知识点】扇形面积的计算
28. 【答案】
(1) ;
(2) 连接 .
由格点可知,,
所以 ,
所以 ,
所以 旋转到 经过路线长为:.
【解析】
(1) 连接 ,
因为 ,,
所以 中点为 ,
所以 ,
所以 中垂线解析式:
,
,
连接 .
的中垂线为:.
所以当 代 ,
所以 ,
所以 ,
如图 ,
因为 ,,,
所以 ,
所以旋转角度为 .
【知识点】坐标平面内图形的旋转变换、弧长的计算
一、选择题
圆心角为 的扇形的半径为 ,则这个扇形的面积是
A. B. C. D.
若扇形的圆心角为 ,半径为 ,则该扇形的弧长为
A. B. C. D.
已知圆的半径为 ,扇形的圆心角为 ,则扇形的面积为
A. B. C. D.
如图,点 是以 为直径的半圆 的三等分点,,则图中阴影部分的面积是
A. B. C. D.
半径为 的圆在长为 、宽为 的长方形内滚动,则该圆滚动过程中所能覆盖部分的最大面积等于
A. B. C. D.
如图,正六边形 内接于 , 的半径为 ,则这个正六边形的边心距 和 的长分别为
A. , B. , C. , D. ,
如图,已知 的半径是 ,点 ,, 在 上,若四边形 为菱形,则图中阴影部分面积为
A. B. C. D.
如图,扇形 的半径为 ,,以 为直径画半圆,则图中阴影部分的面积为
A. B. C. D.
如图,四边形 是菱形,,,扇形 的半径为 ,圆心角为 ,则图中阴影部分的面积是
A. B. C. D.
如图,在矩形 中,已知 ,,矩形的对角线长为 ,矩形在直线 上绕其右下角的顶点 向右旋转 至图①位置,再绕右下角的顶点继续向右旋转 至图②位置,以此类推,这样连续旋转 次后,顶点 在整个旋转过程中所经过的路程之和是
A. B. C. D.
二、填空题
一条弧所对的圆心角为 ,弧长等于半径为 的圆的周长的 倍,则这条弧的半径为 .
把如图①所示的半径为 的圆分割成四段相等的弧,再将这四段弧依次相连拼成如图②所示的恒星图形,那么这个恒星图形的面积等于 .
如图, 为半圆内一点, 为圆心,直径 长为 ,,,将 绕圆心 逆时针旋转至 ,点 在 上,则边 扫过区域(图中阴影部分)的面积为 .
如图 ,分别以等边三角形 的三个顶点为圆心,以边长 为半径画弧 ,,,我们将这三条弧所组成的封闭图形称为莱洛三角形.
()若 ,则莱洛三角形的面积(即封闭图形面积)为 .
()如图 ,将一个莱洛三角形放置于直角坐标系 轴上方,其“底端”落在原点 处,一顶点及中心 在 轴正半轴上,如使莱洛三角形沿 轴正向滚动前进,在滚动过程中莱洛三角形每时每刻都有一个“最高点”,其中心也在不断移动位置如果在莱洛三角形滚动一周的过程中,将其“最高点”和“中心点”所形成的轨迹图形按上、下放置,应大致为下列选项中 的形状.
A.
B.
C.
D.
如图,已知 , 是以 为直径的半圆周上的两点, 是圆心,半径 ,,则图中阴影部分的面积等于 .
如图,在 中,,,,两等圆 , 外切,那么图中两个扇形(即阴影部分)的面积之和为 .(保留 ).
如图,六边形 是正六边形,曲线 叫做“正六边形的渐开线”,,,,,,, 的圆心依次按 ,,,,, 循环,且每段弧所对的圆心角均为正六边形的一个外角.当 时,曲线 的长度是 .
如图,在扇形 中,, 平分 交 于点 ,点 为半径 上一动点.若 ,则阴影部分周长的最小值为 .
三、解答题
如图,有一直径是 米的圆形铁皮,要从中剪出一个圆心角是 的扇形 .求:
(1) 被剪掉阴影部分的面积;
(2) 若用所留的扇形铁皮围成一个圆锥,该圆锥底面圆的半径是多少米?
如果圆的面积为 ,那么圆心角为 的扇形面积是多少?
已知扇形的圆心角为 ,半径为 厘米,求这个扇形的周长和面积.
如图,在平面直角坐标系 中,点 ,,.
(1) 以点 为旋转中心,把 逆时针旋转 ,画出旋转后的 .
(2) 在()的条件下,
①点 经过的路径的长度为 (结果保留 ).
②点 的坐标为 .
有一副大小齿轮互相啮合,大齿轮的半径为 毫米,小齿轮的半径是 毫米,则小齿轮转动一周时,大齿轮转动的角度是多少?
如图,在网格中将 绕点 逆时针旋转 得到 .
(1) 在网格中作出 ;(不要求写作法)
(2) 设网格中小正方形的边长均为 ,求线段 扫过的面积.(结果保留 )
回答下列问题:
(1) 如图,已知线段 上有两点 , 且 ,点 , 分别为 , 的中点, 厘米.求 的长.
(2) 如图,圆 的直径为 ,两条直径 , 相交成 角,, 是 的平分线.
①求 的度数;
②求扇形 的面积.
如图,直线 与双曲线 交于 , 两点,与 , 轴分别交于 , 两点,且 .
(1) 求一次函数和反比例函数解析式;
(2) 若点 与点 关于 轴对称,连接 ,,求 的面积.
如图,在扇形 中,,, 是 的中点, 于点 ,交 于点 ,以 为半径的 交 于点 .求图中涂色部分的面积.
如图,在平面直角坐标系 中, 由 绕点 顺时针旋转得到,且顶点都在格点上.
(1) 点 的坐标为 ,旋转角度为 .
(2) 求点 旋转到 所经过的路线长.
答案
一、选择题(共10题)
1. 【答案】D
【解析】.
【知识点】扇形面积的计算
2. 【答案】C
【知识点】弧长的计算
3. 【答案】C
【解析】 扇形的圆心角为 ,其半径为 ,
.
【知识点】扇形面积的计算
4. 【答案】A
【解析】连接 ,
点 是以 为直径的半圆 的三等分点,
,,
为半圆的直径,
,
,
的面积 的面积 ,
扇形 的面积 ,
则阴影部分的面积 ,故选:A.
【知识点】扇形面积的计算
5. 【答案】B
【知识点】扇形面积的计算
6. 【答案】D
【解析】如图所示,连接 ,,
多边形 是正六边形,
,
,
是等边三角形,
,
,
的长 .
【知识点】弧长的计算
7. 【答案】B
【解析】连接 和 交于点 ,如图所示:
圆的半径为 ,
,
又四边形 是菱形,
,,
在 中,利用勾股定理可知:,,
,
,,
,
,
则图中阴影部分面积为 .
【知识点】扇形面积的计算
8. 【答案】C
【知识点】扇形面积的计算
9. 【答案】A
【解析】连接 .
四边形 是菱形,,
,
,
是等边三角形,
,
的高为 ,
扇形 的半径为 ,圆心角为 ,
,,
,
设 , 相交于点 ,设 , 相交于点 ,
在 和 中,
,
四边形 的面积等于 的面积,
图中阴影部分的面积是:.
【知识点】扇形面积的计算、菱形的性质
10. 【答案】D
【知识点】弧长的计算
二、填空题(共8题)
11. 【答案】
【知识点】弧长的计算
12. 【答案】
【解析】如图,
新的正方形的边长为 ,
恒星图形的面积 ,
故答案为 .
【知识点】扇形面积的计算
13. 【答案】
【解析】 , 是 绕圆心 逆时针旋转得到的,
,,
,,
,
,
,
,,
,.
【知识点】扇形面积的计算
14. 【答案】 ;B
【解析】()过 作 于 ,
因为 是等边三角形,
所以 ,,
因为 ,
所以 ,,
所以 的面积为 ,
,
所以莱洛三角形的面积 .
故答案为:.
()由题意,最高点到 轴的距离是不变的,中心点 到 轴的距离开始是增加然后减小,再增加,又减小,不断循环.
故图象选B.
故选B.
【知识点】弧长的计算
15. 【答案】
【解析】
答:图中阴影部分的面积等于 .
【知识点】扇形面积的计算
16. 【答案】
【知识点】扇形面积的计算、圆与圆的位置关系
17. 【答案】
【知识点】弧长的计算
18. 【答案】
【知识点】弧长的计算、找动点,使距离之和最小
三、解答题(共10题)
19. 【答案】
(1) 连接 ,,,
,,
.
又 ,
,
是等边三角形,
米,
(平方米),
(平方米).
(2) 在扇形 中, 的长为 (米).
设底面圆的半径为 米,则 ,
,
该圆锥底面圆的半径是 米.
【知识点】扇形面积的计算、图形初步、圆锥的表面积计算
20. 【答案】 .
【知识点】扇形面积的计算
21. 【答案】 厘米, 平方厘米.
【知识点】弧长的计算、扇形面积的计算
22. 【答案】
(1) 如图所示, 即为所求.
(2) ;
【解析】
(2) ① ,,
点 经过的路径的长为 ,
故答案为:.
②由图知点 的坐标为 .
故答案为:.
【知识点】坐标平面内图形的旋转变换、弧长的计算、勾股定理
23. 【答案】 .
【知识点】弧长的计算
24. 【答案】
(1) 如答图 所示.
(2) 由题意得 ,则线段 扫过的面积为 .
【知识点】扇形面积的计算、作图-旋转变换
25. 【答案】
(1) ,
设 ,,,
, 分别是 , 的中点,
,
,
,
.
(2) ① ,,
,
是 的平分线,
,
两条直径 , 相交成 角,
;
② 的面积 ,
扇形 的面积 .
【知识点】扇形面积的计算、线段的和差、角的计算
26. 【答案】
(1) ,
,
,
,
,
把 , 分别代入 ,得
解得
一次函数的解析式为 ,
把 代入 ,得 ,
.
把 代入 ,得 ,
反比例函数的解析式为 .
(2) 点 与点 关于 轴对称,由()知 ,
,
,
解方程组 得
,
,
,
【知识点】一次函数的解析式、坐标平面内图形的面积、反比例函数的解析式、反比例函数与方程、不等式
27. 【答案】如图,连接 ,,
,
,
为 的中点,,
,,
,
为等边三角形,
,
在 中,由勾股定理,得 ,
【知识点】扇形面积的计算
28. 【答案】
(1) ;
(2) 连接 .
由格点可知,,
所以 ,
所以 ,
所以 旋转到 经过路线长为:.
【解析】
(1) 连接 ,
因为 ,,
所以 中点为 ,
所以 ,
所以 中垂线解析式:
,
,
连接 .
的中垂线为:.
所以当 代 ,
所以 ,
所以 ,
如图 ,
因为 ,,,
所以 ,
所以旋转角度为 .
【知识点】坐标平面内图形的旋转变换、弧长的计算
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
